Atom Interferometers Warm Up
Today, atom interferometry is among the most advanced technologies for high-precision measurements. It is applied, for instance, to build absolute gravimeters [1], investigate the variation of the fine structure constant [2], measure rotation rates [3], and test the equivalence principle [4]. Its sensitivity stems from the fact that cold massive particles can behave like coherent waves, characterized by a wavelength determined by the particles’ momenta. To achieve and maintain the coherence required for interferometric measurements, most setups use complex laser cooling and trapping methods that keep atomic ensembles at temperatures in the microkelvin range. But now, Grant Biedermann at the Sandia National Laboratories in New Mexico and co-workers [5] have demonstrated an atom interferometer that instead uses a warm vapor enclosed in a glass cell. Removing the need for ultrahigh vacuum and laser cooling schemes, the result reverses the current trend towards colder temperatures in atom interferometry, posing an important step towards field applications [6] but also enlarging the technology playground of quantum sensors.
Atom interferometers are based on the same principles as optical interferometers: After propagating along two separate paths, matter waves recombine, and may interfere constructively or destructively. The interference generates fringes that carry information on effects, such as gravity, that modify the phase of the wave function that describes the propagating atoms. Because atoms in an interferometer move at much slower velocities than light, they are influenced by the effects that alter their phase on a much longer time scale. This makes atom interferometers much more sensitive than optical ones.
One of the leading atomic interferometry techniques is light-pulse atom interferometry (LPAI). LPAI schemes typically start with clouds of atoms laser cooled to temperatures as low as millionths of a degree kelvin. Laser pulses are then used to control the external degrees of freedom (position, velocity) of the cold atoms via the coupling of the atoms’ internal degrees of freedom (different magnetic and hyperfine states) to light. Such pulses can effectively work both as beam splitters that separate the atoms and as mirrors that deflect them, allowing the realization of interferometric geometries [7].
Conventional LPAI requires large ensembles of ultracold atoms with narrow velocity distributions that are isolated from the environment. This is only achievable through laser cooling schemes in ultrahigh vacuum chambers. Would it be possible to produce and exploit matter-wave interference phenomena using hot atoms kept in a simple vapor cell? Vapor-cell approaches have previously been used in atomic clocks [8] and magnetometers operated at room temperature. But the extension to more general atom interferometers faces two challenges. The first is the loss of atomic spin polarization due to atom-atom collisions and to collisions between the atoms and the walls of the cell in which they are housed. The second is the random thermal motion of the atoms, which makes it difficult to create and preserve coherent matter-wave-packet superpositions. Biedermann and co-workers have devised a clever scheme that addresses these two challenges.
To solve the problem of spin-polarization loss, the researchers borrow a trick previously used in vapor-cell sensors [9]. When an atom collides with the walls of the vapor cell, its spin can flip due to the electromagnetic fields generated by unsaturated bonds in the cell’s walls. Atoms whose spin has been flipped would then not be able to contribute to the interference signal. To hinder this effect, the team deposited a low-vapor-pressure spin antirelaxation coating onto the cell’s walls, which passivates unsaturated chemical bonds and thus removes spurious fields. This solution reduces the loss in spin polarization to just 10%.
To tackle the problems deriving from the atoms’ thermal agitation, Biedermann and co-workers selected, within a broad distribution of velocities, only atoms with two well-defined velocity classes. So, instead of preparing cold atomic ensembles with narrow velocity distributions as in conventional LPAIs, the new scheme extracts a subset of atoms from a thermal ensemble. The difference between cold LPAIs and Biedermann et al.’s setup can be illustrated with an analogy from optical interferometry. LPAI interferometry with coherent atomic matter waves is similar to optical interferometry with a coherent light source—a laser. Doing interferometry with a warm vapor, on the other hand, is like searching for interferometric effects using the white incoherent light from a common light bulb.
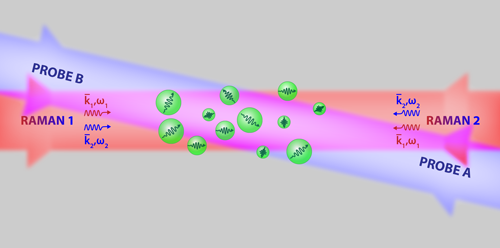
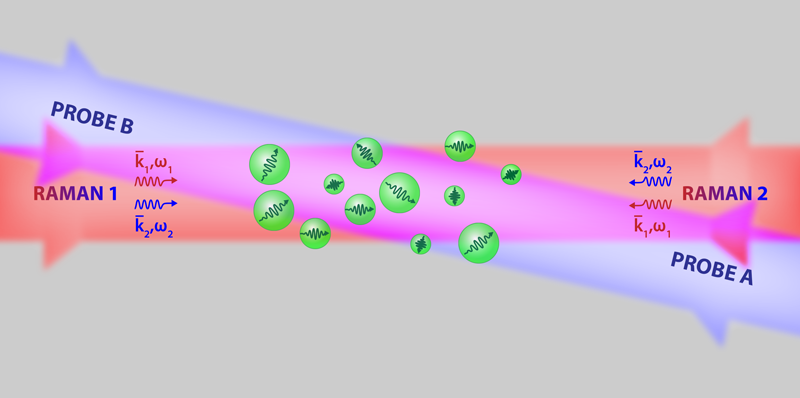
To select the two subsets of atoms, the researchers use two counterpropagating Raman lasers that simultaneously excite two groups of atoms with opposite velocity, +𝜈z and −𝜈z, along the laser propagation directions (Fig. 1), where 𝜈z depends on the frequency of the Raman beams. After selection, the same Raman lasers “kick” the atoms in a three-pulse sequence that generates two different paths in a so-called Mach-Zehnder interferometric configuration.
The difficulty of these experiments is determining the phase difference of the two interfering atom waves from the fringes measured in a warm system with an extremely short coherence length. The solution presented by Biedermann and co-workers consists of simultaneously detecting the two atomic groups ( +𝜈z and −𝜈z) participating in the interferometer. The authors use two additional counterpropagating probe beams (Fig. 1) that measure a differential signal from which the phase difference is extracted. One can show that the two interferometers possess equal and opposite sensitivity to the atoms’ acceleration. The differential signal eliminates noise and offsets that are present in both channels, doubling at the same time the sensitivity to accelerations.
The Raman lasers “interrogate” the hot atoms for a time limited by the average transit time of the atoms across these beams. Because of the atoms’ thermal velocities, this sets the biggest limitation to this scheme, dramatically reducing the interferometer phase sensitivity compared to cold LPAIs. Using the maximum available interrogation time of 15𝜇s, this work demonstrates an acceleration sensitivity of 10−2g∕√Hz (where g is the local gravitational acceleration on Earth, approximately 9.8m s−2)—five orders of magnitude worse than the current state-of-the-art of atom-interferometry acceleration measurements [1, 10]. However, sensitivity is not the only parameter of relevance for applications, and the new scheme offers two important advantages over cold schemes. The first is that it can acquire data at a rate of 10 kHz [11], in contrast to the typical 1-Hz rate of cold-atom LPAIs. The second advantage is the broader range of accelerations that can be measured with the same setup. This vapor-cell sensor remains operational over an acceleration range of 88g, several times larger than the typical range of cold LPAIs.
The large bandwidth and dynamic range of the instrument built by Biedermann and co-workers may enable applications like inertial navigation in highly vibrating environments, such as spacecraft or airplanes. What’s more, the new scheme, like all LPAIs, has an important advantage over devices like laser or electromechanical gyroscopes: it delivers acceleration measurements that are absolute, without requiring a reference signal. This opens new possibilities for drift-free inertial navigation devices that work even when signals provided by global satellite positioning systems are not available, such as in underwater navigation.
This research is published in Physical Review Letters.
References
- P Gillot et al., “Stability Comparison of Two Absolute Gravimeters: Optical Versus Atomic Interferometers,” Metrologia 51, L15 (2014).
- P. Cladé et al., “Determination of the Fine Structure Constant Based on Bloch Oscillations of Ultracold Atoms in a Vertical Optical Lattice,” Phys. Rev. Lett. 96, 033001 (2006).
- I. Dutta et al., “Continuous Cold-Atom Inertial Sensor with 1 nrad/sec Rotation Stability,” Phys. Rev. Lett. 116, 183003 (2016).
- H. Müntinga et al., “Interferometry with Bose-Einstein Condensates in Microgravity,” Phys. Rev. Lett. 110, 093602 (2013).
- G. W. Biedermann et al., “Atom Interferometry in a Warm Vapor,” Phys. Rev. Lett. 118, 163601 (2017).
- 𝜇QuanS (www.muquans.com); AOSense (www.aosense.com).
- Ch.J. Bordé, “Atomic Interferometry with Internal State Labelling,” Phys. Lett. A 140, 10 (1989).
- S. Knappe et al., “A Microfabricated Atomic Clock,” Appl. Phys. Lett. 85, 1460 (2004).
- S. J. Seltzer et al., “Investigation of Antirelaxation Coatings for Alkali-Metal Vapor Cells Using Surface Science Techniques,” J. Chem. Phys. 133, 144703 (2010).
- Z.-K. Hu et al., “Demonstration of an Ultrahigh-Sensitivity Atom-Interferometry Absolute Gravimeter,” Phys. Rev. A 88, 043610 (2013).
- A. V. Rakholia, H. J. McGuinness, and G. W. Biedermann, “Dual-Axis High-Data-Rate Atom Interferometer via Cold Ensemble Exchange,” Phys. Rev. Applied 2, 054012 (2014).