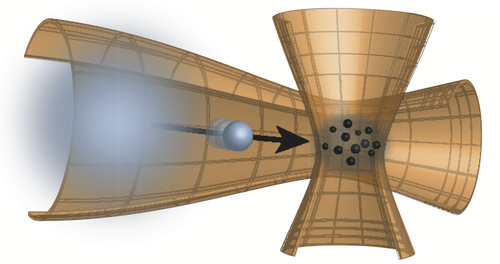
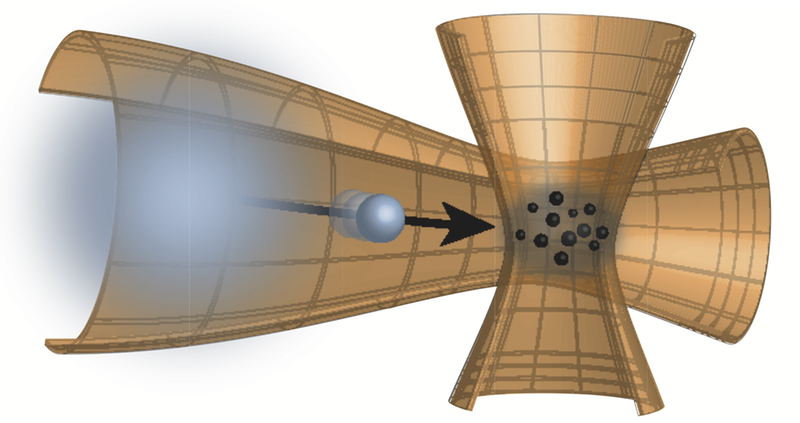
Observing Diffusion Atom by Atom
Diffusion—the process by which small particles disperse within a fluid medium—describes a wide range of phenomena, such as the spreading of pollen and dust in the atmosphere and the mixing of two liquids. A team in Germany has now been able to follow individual atoms diffusing through a thin gaseous medium. They find that just a single collision is enough to bring an atom close to equilibrium with other atoms in the medium. The results could help in modeling diffusion in rarefied environments, such as interstellar space.
Diffusion was first explained at the microscopic level by Albert Einstein, who showed in a 1905 paper that a diffusing particle should follow a random, meandering path, called Brownian motion, owing to collisions with the molecules of the surrounding medium. In early studies, the particles were much larger than the molecules, so billions of collisions were typically needed to change the particle’s path. “This can be compared to the situation of a cargo ship in a ball pit,” says Artur Widera of the University of Kaiserslautern in Germany.
For relatively large particles, one need not track every collision. Instead, the collective effect of impacts can be modeled as a randomly fluctuating force, along with a viscosity that accounts for a particle’s energy loss to the surroundings. Combining these two effects in a modified Newtonian equation, called the Langevin equation, allows researchers to calculate many of the particle’s properties of interest, such as how its average velocity evolves over time.
But what if the individual collisions are more significant—if the diffusing particle is more like another ball than a ship? That, after all, is more like the situation when gases or liquids mix. To track the effect of individual collisions, Widera and colleagues studied the diffusion of just a few cesium (Cs) atoms within a rarefied cloud of several thousand rubidium (Rb) atoms.
The researchers held the cloud within an optical trap and cooled it to just a few millionths of a degree Kelvin above absolute zero. They then fired Cs atoms one by one into the cloud with a specified energy. Under these conditions, the gas is so dilute that collisions of a Cs atom with the Rb medium are rare, happening on average every tenth of a millisecond or so.
After a certain time delay, Widera and colleagues “froze” the positions of a handful of Cs atoms by turning on another light field that immobilized them within a grid of tiny trapping sites. They then recorded the positions of the trapped atoms using a laser beam that makes Cs atoms emit light.
By using different delay times between the introduction of the Cs atoms and the freezing, the researchers could discern how, on average, the atoms’ motions were altered by collisions with the Rb atoms in the surrounding vapor. In their data, they were able to identify a “thermalized” group of Cs atoms whose motion was more or less randomized by collisions. They showed that one collision was enough to knock an atom into this group. Using computer simulations, the researchers deduced that such a collision can strip more than half of the Cs atom’s initial kinetic energy.
These experimental conditions—in which collisions happen rarely, but each one has a huge impact—are very far from the usual diffusion situation for which the Langevin equation applies. In this case, Widera says, “everybody, including me initially, would bet that a Langevin description would fail miserably.”
But surprisingly, the researchers found that, once a Cs atom has undergone a single collision and begun to thermalize, the Langevin equation works well with just a single modification: letting the effective viscosity of the medium depend on the velocity of the diffusing atom. Such a simple, modified Langevin description could describe diffusion in some important real-world situations, such as diffusion of aerosols in the upper atmosphere or of gas in interstellar space.
“This is certainly a nice study,” says theoretical physicist Udo Seifert of the University of Stuttgart in Germany. It comes as a surprise that the standard Langevin equation works with such a minor modification, he says. Atomic physicist David Weiss of Pennsylvania State University in University Park points out that collision dynamics between similar-sized objects is “well understood classical physics” taught in most first-year physics classes. But, he adds, these new results uniquely disclose the process at the level of single atoms.
This research is published in Physical Review Letters.
–Philip Ball
Philip Ball is a freelance science writer in London. His latest book is How Life Works (Picador, 2024).