Tube Model Under Tension
Polymers are the extremely long, stringy molecules inside many of the materials around us. Sitting in my office I might glance down at my pen, my telephone, my computer monitor, my chair, and so on. They all contain plastics, and so all contain polymers. Plastics are versatile and useful because they can be processed easily—they can be stretched, pulled, and squeezed into any shape we desire. But what happens to the stringy polymers in such processing? Understanding the shapes that the polymers are forced into when their host materials are processed is key to controlling the processing. In a new study, Yangyang Wang at Oak Ridge National Laboratory in Tennessee and co-workers [1] have used neutron scattering as a microscope to see the shape of polymers within samples under deformation. The results of their novel data analysis provide a “fingerprint” of the molecular deformation, and they claim that their results challenge the dominant “tube model” of polymer flow.
The tube model is arguably the most successful theory of modern soft-matter physics, having provided a picture for understanding polymer motion for about 50 years. Pioneered by Pierre-Gilles de Gennes [2] and Masao Doi and Sam Edwards [3], the theory now enables practical predictions for manufacturing and processing of industrial plastic materials [4]. The model is easy to visualise. In polymeric materials, the long molecules become tangled with each other—like intertwined spaghetti—and these “entanglements” restrict the molecular motion. A molecule can move easily along the direction of its length, but motion perpendicular to it is strongly suppressed because this involves traversing other molecules, which would break interatomic bonds. The tube model pictures this motion by assuming the polymer is trapped within a “tube” of entanglements, so that the molecule is only able to move along the contour of that tube. This inspired guess allows the polymer motion to be described mathematically in equilibrium and strong-deformation conditions, predictions to be made, and materials to be successfully modeled.
The tube model works well at describing polymeric materials under small deformations. For these conditions, it is sufficient to describe only the thermal Brownian motion of the polymer strings subject to the constraints from entanglements. This is the back-and-forth random motion of the polymers along their tube contour, which de Gennes called reptation [2] in analogy to the motion of a snake. Early predictions of the response of the material to small deformations using this description were not perfect. It took many refinements to this basic model, such as accounting for fluctuations of the length of the strings along the tube, before a fully quantitative theory was derived [5].
But the real difficulty in describing polymer flow comes when the material is strongly deformed. What then happens to the entanglements and to the tube? Do these survive the deformation, and if so, how? The truth is, nobody knows. But this has not prevented further inspired guesses from being made. Doi and Edwards [3] made one of the earliest such guesses. They claimed that the polymer strings, and the tubes surrounding them, would be stretched “affinely” with the material, that is, in direct proportion to the material deformation. As a result, the length of the polymers along the contour of their tubes must increase on average. Doi and Edwards predicted that the first response of the molecules after the deformation must be to “retract” back until they are once again at their equilibrium length in the tube. Because the tube model assumes that all polymer motion is constrained by entanglements, this retraction can only occur along the tube contour. This gives a very characteristic and specific prescription for how the shapes of the polymers change after deformation: the size of the molecules should decrease in all directions during the retraction process, and any experiment that can detect the molecular size should be able to confirm this retraction. This is where the neutron-scattering experiments of Wang and colleagues [1] come in.
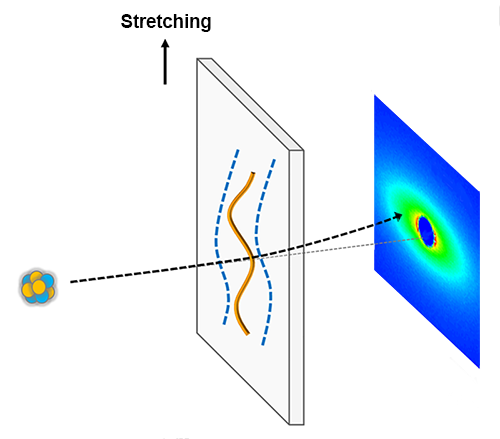
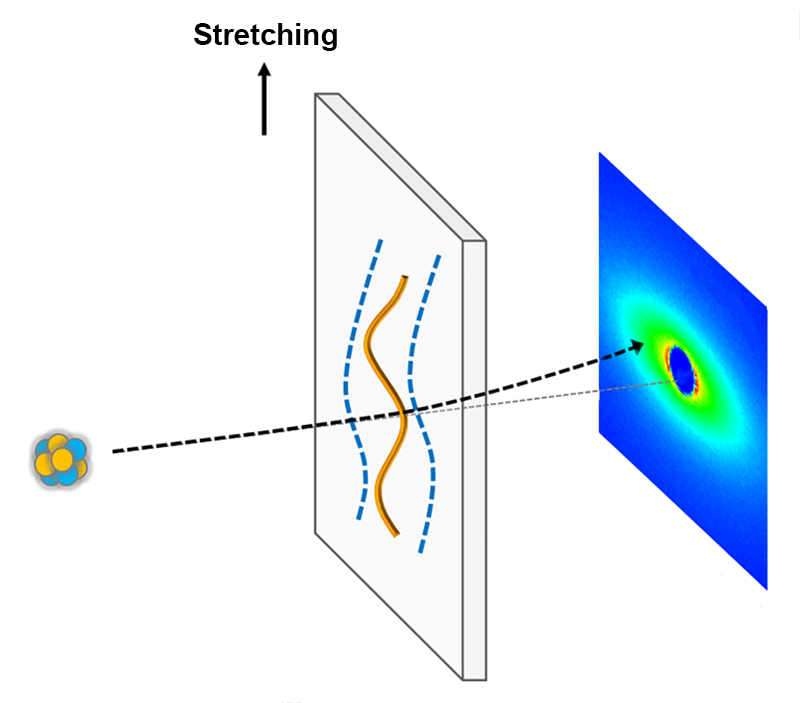
Neutron scattering is an excellent method to study the molecular size. It usually involves a mixture of molecules, in this case a mixture of polymers, in which most of the molecules have their hydrogen atoms replaced by deuterium, while a small fraction of the molecules are labeled by retaining their hydrogen atoms. The labeled and unlabeled polymers scatter the neutron beam by different amounts, and the resulting two-dimensional diffraction pattern is a measure of the polymer size and shape. In their study, Wang and co-workers stretched a series of such mixtures, waited for various times following the stretch before freezing the molecules in place by cooling, and finally fired the neutron beam through the materials (Fig. 1) to obtain a collection of diffraction patterns. They expected to see the characteristic decrease in polymer size from the retraction process, but they found no evidence of retraction, in contradiction to tube-model expectations.
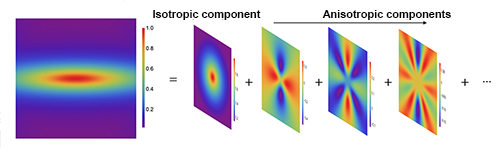
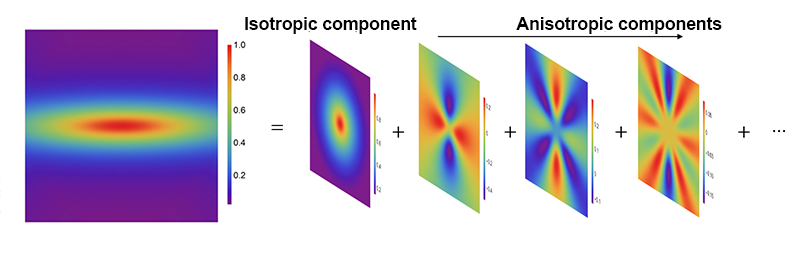
They are not the first group to attempt to see retraction using neutron-scattering data: Boué and co-workers tried but did not see the retraction [6]; and I was involved in a collaboration [7] that did seem to observe the retraction. What sets Wang and colleagues’ work apart is their novel data analysis. The researchers decomposed each of the two-dimensional diffraction patterns into a sum over spherical harmonic contributions (Fig. 2). This allowed them to make use of all the data to extract the important anisotropic components of the scattering for different scattering angles, giving information about the degree of deformation of the polymers on different size scales. These scattering components can be carefully compared with theoretical expectations. Previous analyses focused primarily on the data parallel or perpendicular to the deformation direction, using a fraction of the available data.
What might this mean, and what will happen next? Wang and colleagues’ paper is one of several recent papers to take aim at the tube model (see, for example, Ref. [8]); on many occasions the model has withstood the criticism (see, for instance, Ref. [9]). There is also the paper I co-authored [7], which did claim to observe retraction. Setting potential experimental artefacts aside, one distinction of our work was that our polymers had a significantly larger number of entanglements, and there are several corrections to the theory that may disrupt the observation of retraction for a smaller number of entanglements. Still, the challenge is there, and it is clear: can tube theorists such as myself successfully explain why Wang and colleagues did not observe retraction, and can we predict the fine details revealed by their novel data analysis? Or, should we modify, or even jettison, the tube theory? The next steps will most likely be to re-examine the tube-model calculations and the approximations made along the way to derive the final theoretical results.
This research is published in Physical Review X.
References
- Z. Wang, C. N. Lam, W.-R. Chen, W. Wang, J. Liu, Y. Liu, L. Porcar, C. B. Stanley, Z. Zhao, K. Hong, and Y. Wang, “Fingerprinting Molecular Relaxation in Deformed Polymers,” Phys. Rev. X 7, 031003 (2017).
- P. G. de Gennes, “Reptation of a Polymer Chain in the Presence of Fixed Obstacles,” J. Chem. Phys. 55, 572 (1971).
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics (Clarendon Press, Oxford, 1986)[Amazon][WorldCat].
- D. J. Read, “From Reactor to Rheology in Industrial Polymers,” J. Polym. Sci., Part B: Polym. Phys. 53, 123 (2014).
- A. E. Likhtman and T. C. B. McLeish, “Quantitative Theory for Linear Dynamics of Linear Entangled Polymers,” Macromolecules 35, 6332 (2002).
- F. Boué, M. Nierlich, G. Jannink, and R. Ball, “Polymer Coil Relaxation in Uniaxially Strained Polystyrene Observed by Small Angle Neutron Scattering,” J. Phys. 43, 137 (1982).
- A. Blanchard, R. S. Graham, M. Heinrich, W. Pyckhout-Hintzen, D. Richter, A. E. Likhtman, T. C. B. McLeish, D. J. Read, E. Straube, and J. Kohlbrecher, “Small Angle Neutron Scattering Observation of Chain Retraction after a Large Step Deformation,” Phys. Rev. Lett. 95, 166001 (2005).
- P. E. Boukany, S.-Q. Wang, and X. Wang, “Step Shear of Entangled Linear Polymer Melts: New Experimental Evidence for Elastic Yielding,” Macromolecules 42, 6261 (2009).
- O. S. Agimelen and P. D. Olmsted, “Apparent Fracture in Polymeric Fluids Under Step Shear,” Phys. Rev. Lett. 110, 204503 (2013).