Quantum Phase Transitions Go Dynamical

Victor Gurarie

Viewpoint

Quantum Phase Transitions Go Dynamical

Department of Physics, University of Colorado, Boulder CO 80309, USA
School of Physics and Astronomy, Monash University, VIC 3800, Australia

August 21, 2017• Physics 10, 95

The observation of dynamical quantum phase transitions in an interacting many-body system breaks new ground in the study of matter out of thermal equilibrium.

Figure caption — **Figure 1:** Blatt and colleagues [1] have observed dynamical quantum phase transitions in a linear string of $N$ calcium-40 ions, with $N$ up to 10. They measured the so-called rate function of the system as a function of time for $N = 6$ , $N = 8$ , and $N = 10$ . The singularities at two certain critical times that the measured function exhibited indicate that dynamical quantum phase transitions occurred at these times.

Understanding matter—a collection of many interacting constituents, such as atoms and electrons—is a major endeavor in physics. While most studies in this field have focused on matter that is in thermal equilibrium with its environment, many phenomena occurring in nature involve matter out of equilibrium. The reason for this disparity may lie in the often-repeated observation that, to paraphrase Leo Tolstoy’s quote about happy and unhappy families, all forms of equilibrium matter are alike whereas every form of nonequilibrium matter seemingly behaves in its own way. It’s easy to take a model describing interacting atoms, run it on the computer, and study its nonequilibrium behavior. But it’s much harder to describe classes of nonequilibrium phenomena. Rainer Blatt from the Austrian Academy of Sciences and the University of Innsbruck, Austria, and colleagues [1] have now succeeded in observing one such class of phenomena—dynamical quantum phase transitions—in a quantum many-body spin system. These transitions are similar to those that take place when ice melts or water evaporates, but they are not driven by external factors such as temperature. Instead, they are triggered by internal changes in a nonequilibrium quantum system as it evolves in time.

Matter studied in labs equilibrates quickly with the environment with which it typically interacts. The environment is usually held at some temperature, so matter in the lab equilibrates at this temperature. By contrast, artificially engineered quantum matter made up of many atoms or ions at temperatures close to absolute zero, such as an atomic Bose-Einstein condensate, is generally thermally isolated from the environment and can be easily taken out of equilibrium. This feature of engineered quantum matter has made it both the focus and motivator of recent research on nonequilibrium matter.

In particular, recent theoretical work [2] put forward a new class of phenomena that nonequilibrium quantum many-body systems may exhibit. The authors of this 2013 study noted an analogy between the evolution operator—a mathematical operator that describes the evolution of the wave function of a quantum system—and the partition function, which describes the statistical properties of a system in thermal equilibrium with the environment. In this analogy, the role of time in the evolution of a thermally isolated quantum system is equivalent to that of the inverse of the temperature in a system in thermal equilibrium. This equivalence has been known and widely used since the early days of quantum mechanics [3]. But the 2013 study pointed out a previously unexplored consequence of the analogy: just as thermal-equilibrium systems can undergo phase transitions as their temperature is varied, isolated quantum systems that are driven out of equilibrium can experience phase transitions as time marches forward. These dynamical quantum phase transitions—as the authors dubbed this class of nonequilibrium phenomena—would manifest themselves in discontinuous behavior of the system at certain critical times.

These researchers [2] explored this notion in the much-studied one-dimensional transverse-field Ising model, a chain of interacting quantum spins in a transverse magnetic field [4]. This model is known to undergo a standard quantum phase transition between its ordered and disordered spin phases as parameters in the model that describe the spin-spin interactions are changed [5]. This transition occurs in thermal-equilibrium conditions. But the researchers found that if the model is “quenched,” that is, if the values of its parameters are suddenly changed from those corresponding to the ordered phase to those of the disordered phase while the model remains thermally isolated, it will undergo dynamical phase transitions at certain critical times after the quench.

This is exactly what Blatt and colleagues observed in their experimental study of a quantum many-body spin system. The result comes on the heels of a series of studies that realized the transverse-field Ising model using a chain of ultracold ions [6, 7]. Obtained in this way, the model features long-range interactions between the ions, in contrast to the short-range interactions that characterize the original transverse-field Ising model. But as it turns out, this long-range property is irrelevant for the system’s dynamical phase transitions.

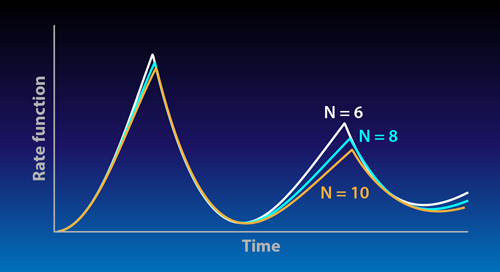
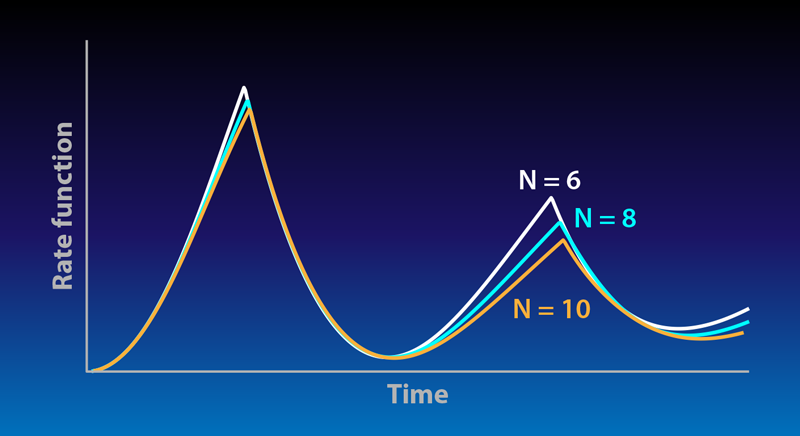
The team created this modified version of the transverse-field Ising model using a linear string of (up to 10) calcium-40 ions. They first prepared the string in the ordered spin state, in which all ion spins point in the same direction. They then suddenly switched on interactions among the spins such that the chain, if it were in equilibrium, would be in a disordered state in which the spins are randomly oriented. This sudden change drove the system out of equilibrium. Next, the system was allowed to evolve freely in time. Finally, the team measured the probability that either all the spins pointed in the same original direction some time after the switch, or they all pointed in the opposite direction. This either/or probability is equivalent to the probability that the sudden change in the interaction parameters involved no thermodynamic work. Theorists have predicted [8] that the evolution of this probability in time would be singular (that is, not a smooth function of time) at certain critical times as a consequence of dynamical phase transitions expected in this system. The probability measured by Blatt and co-workers—or more accurately the so-called rate function, which is closely related to the probability—displays exactly these singularities in time (Fig. 1), confirming the theoretical prediction.

Meanwhile, two papers posted on the arXiv have also described experimental searches for dynamical phase transitions [9, 10]. One of the papers reported a somewhat different signature of dynamical phase transitions in a system of ultracold atoms in an optical lattice [9]. And the other reported additional signatures of dynamical phase transitions in a transverse-field Ising chain made of 53 ions [10]. Clearly, researchers are actively on the hunt for dynamical quantum phase transitions. It remains to be seen whether they are as ubiquitous and as rich in their properties as their equilibrium counterparts. Yet, a predicted class of nonequilibrium phenomena has been brought to the experimental realm. This may well be the beginning of an exciting chapter in the study of nonequilibrium matter.

This research is published in Physical Review Letters.

References

P. Jurcevic, H. Shen, P. Hauke, C. Maier, T. Brydges, C. Hempel, B. P. Lanyon, M. Heyl, R. Blatt, and C. F. Roos, “Direct Observation of Dynamical Quantum Phase Transitions in an Interacting Many-Body System,” Phys. Rev. Lett. 119, 080501 (2017).
M. Heyl, A. Polkovnikov, and S. Kehrein, “Dynamical Quantum Phase Transitions in the Transverse-Field Ising Model,” Phys. Rev. Lett. 110, 135704 (2013).
R. P. Feynman and A. R. Hibbs, Quantum Mechanics and Path Integrals (McGraw-Hill Companies, New York, 1965)[Amazon][WorldCat].
P. Pfeuty, “The One-Dimensional Ising Model with a Transverse Field,” Ann. Phys. 57, 79 (1970).
S. Sachdev, Quantum Phase Transitions (Cambridge University Press, Cambridge, 2011)[Amazon][WorldCat].
J. W. Britton, B. C. Sawyer, A. C. Keith, C.-C. J. Wang, J. K. Freericks, H. Uys, M. J. Biercuk, and John J. Bollinger, “Engineered Two-Dimensional Ising Interactions in a Trapped-Ion Quantum Simulator with Hundreds of Spins,” Nature 484, 489 (2012).
R. Islam, C. Senko, W. C. Campbell, S. Korenblit, J. Smith, A. Lee, E. E. Edwards, C.- C. J. Wang, J. K. Freericks, and C. Monroe, “Emergence and Frustration of Magnetism with Variable-Range Interactions in a Quantum Simulator,” Science 340, 6132 (2013).
B. Zunkovic, M. Heyl, M. Knap, and A. Silva, “Dynamical Quantum Phase Transitions in Spin Chains with Long-Range Interactions: Merging Different Concepts of Nonequilibrium Criticality,” arXiv:1609.08482.
N. Fläschner, D. Vogel, M. Tarnowski, B. S. Rem, D.-S. Lühmann, M. Heyl, J. C. Budich, L. Mathey, K. Sengstock, and C. Weitenberg, “Observation of a Dynamical Topological Phase Transition,” arXiv:1608.05616.
J. Zhang, G. Pagano, W. Hess, A. Kyprianidis, P. Becker, H. Kaplan, A. V. Gorshkov, Z.-X. Gong, and C. Monroe, “Observation of a Many-Body Dynamical Phase Transition with a 53-Qubit Quantum Simulator,” arXiv:1708.01044.

About the Author

Victor Gurarie is a Professor of Physics at the University of Colorado Boulder and a member of its Center for Theory of Quantum Matter. He is also an Adjunct Professor of Physics at Monash University in Melbourne, Australia. He works in condensed-matter physics and many-body theory, with an emphasis on applications to ultracold atomic systems. His recent interests include superconductivity with cold atoms, topological states of matter and the quantum Hall effect, and out-of-equilibrium phenomena.