Intermittent Turbulence in a Global Ocean Model
One of the hallmarks of turbulence is intermittent behavior, such as the sudden and unpredictable gusts of wind in the north of Scotland. Intermittency is related to the existence of intense and sparse coherent structures, as in atmospheric fronts, hurricanes, and tornadoes, and to small-scale vortex filaments in fully turbulent flows. Intermittent behavior has been observed in the ocean, but its implications are not fully understood. This is because computer models are unable to incorporate the full range of scales involved: from the planetary scale ( ∼104 km) down to the scale at which energy is dissipated ( ∼1 mm). A new numerical study of the global ocean breaks the problem into two parts by simulating the dynamics at large scales (greater than roughly 1 km) and then approximating how energy cascades to smaller scales [1]. The researchers—Brodie Pearson and Baylor Fox-Kemper from Brown University in Rhode Island—find spatial intermittency in the dissipation of kinetic energy at large scales where one would expect waves to smooth out fluctuations in the flow. The results imply that some regions in the ocean may dissipate much more energy than other regions, which could affect how oceanographers estimate the energy budget of the ocean from localized observations.
Intermittency, as a property of small-scale turbulence, has been known and analyzed for a long time (see, for example, Refs. [2, 3]). In the case of fluid flows, intermittent behavior is characterized by “fat wings” in the probability distribution functions (PDFs) for velocity gradients and temperature gradients in the fluid. These wings imply that sudden velocity or temperature changes occur more often than would be predicted by a bell-shaped, or “normal,” PDF. High-resolution spatial and temporal measurements have revealed small-scale intermittency in many phenomena, such as the dissipation of energy in the atmosphere or the ocean [4, 5], the rain formation process [6], superfluid turbulence [7], and the solar wind [8].
The presence of intermittency in a turbulent system implies a process of large eddies breaking up into smaller eddies. This energy cascade is due to a nonlinear coupling between oscillation modes at different scales. In a system that is three dimensional, homogeneous, and isotropic, the cascade leads to a highly chaotic and spatially complex state called fully developed turbulence [9]. The situation is more complicated in the ocean, where coastlines, tides, and winds play a role. At large scales, the flow is influenced by waves that are generated from the Earth’s rotation and gravity. When these waves are strong, i.e., faster than the turbulent eddies, there arises a so-called geostrophic balance between the Coriolis force, gravity, and pressure gradients. Under these conditions, the fluid acceleration is zero, and the flow should be steady, apart from fluctuations and resonances between waves. And yet, in idealized models where geostrophic balance is assumed, and the fluid motion is stratified in largely separated horizontal layers, researchers have found that the flow is highly intermittent, more so than in fully developed turbulence [10]. In this case, the fat-wing PDFs occur in the vertical velocity and temperature fluctuations themselves, as opposed to only their gradients, which implies large-scale intermittency.
But is large-scale intermittency in the ocean realistic? Or is it a consequence of the assumptions that modelers make? To help answer this question, Pearson and Fox-Kemper [1] performed a large numerical simulation with a global ocean model that includes land masses and some ocean topography. The researchers simplified some of the physics; namely, the fluid dynamics was confined to the two horizontal directions, the pressure at each depth was determined under the assumption of hydrostatic equilibrium, and small scales were treated with several types of modeling. One of the main questions is whether the small-scale modeling affects the outcome, as there is only one truth and several ways to cheat. The authors utilized several commonly used models and found that the main results remain unchanged for the most part.
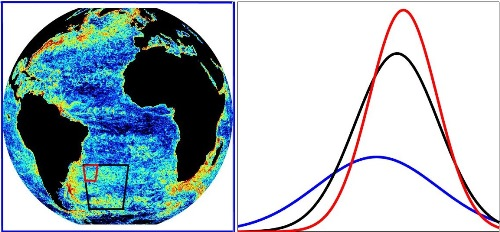
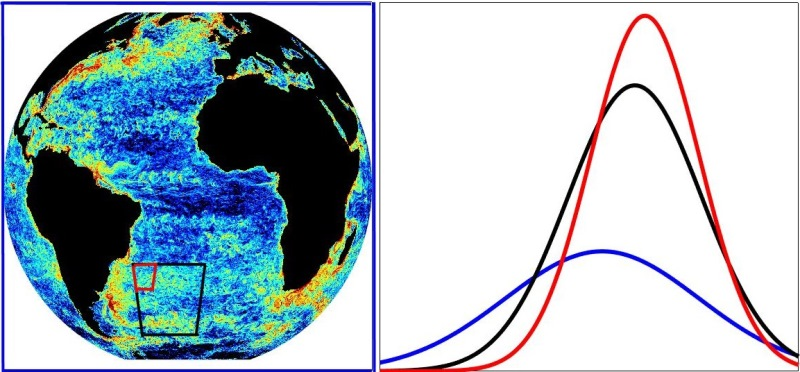
Based on this modeling, Pearson and Fox-Kemper determined a map of local energy dissipation in the ocean (Fig. 1). The map displays a marked spottiness, with dissipation intensities in some locations higher than the mean by several orders of magnitude. The researchers characterized this spatial intermittency by showing that the PDF of the logarithm of the dissipation had a normal (Gaussian) profile. This log-normal behavior, which was observed at all depths of their model ocean, implies a fat-wing distribution in the dissipation. Such a finding has direct consequences for what is inferred for the total energy budget of the ocean when it is evaluated from local oceanic measurements. For example, a 2008 study [5] found that, under the passage of the tide, the local dissipation off the coast of Hawaii is strongly enhanced in the ocean because of the presence of mountainous relief on the oceanic floor.
Pearson and Fox-Kemper say that the log-normal property of ocean dissipation is evidence that energy flux is transmitted from scale to scale at a constant rate, until it’s finally dissipated at small scales. However, there are distributions, such as log-Poisson and log-Lévy distributions, which can also model intermittency. What distinguishes these different distributions is their behavior at small scales. Thus any departure from log-normality in dissipation data would have relevance to the geometry of small-scale structures [9]. The authors analyzed the higher-order moments of their PDF and found behavior that was close, but not identical, to what is expected from log-normal processes.
Accessing higher numerical resolution should allow for more intermittency, which is smoothed out by large grid sizes in the simulations. It remains to be seen whether introducing more accurate dynamics of the small scales will modify the characteristics of the intermittency of the intermediate scales. The answer to this is essential to determine how subgrid modeling must be altered. The authors note that 90% of the dissipation occurs in approximately 10% of the model ocean’s volume, as opposed to being evenly distributed [1]. This concentrated behavior might be turned into an advantage. For example, it could be incorporated in future weather and climate models, to make them more amenable to prediction of extreme fluctuations and their effects on the flow dynamics.
This research is published in Physical Review Letters.
References
- B. Pearson and B. Fox-Kemper, “Log-Normal Turbulence Dissipation In Global Ocean Models,” Phys. Rev. Lett. 120, 094501 (2018).
- A. N. Kolmogorov, “A Refinement of Previous Hypotheses Concerning the Local Structure Of Turbulence in a Viscous Incompressible Fluid at High Reynolds Number,” J. Fluid Mech. 13, 82 (1962).
- B. B. Mandelbrot, “Intermittent Turbulence in Self-Similar Cascades: Divergence of High Moments and Dimension of the Carrier,” J. Fluid Mech. 62, 331 (1974).
- L. Mahrt, “Intermittency of Atmospheric Turbulence,” J. Atmos. Sci. 46, 79 (1989).
- J. M. Klymak, R. Pinkel, and L. Rainville, “Direct Breaking of the Internal Tide near Topography: Kaena Ridge, Hawaii,” J. Phys. Oceanogr. 38, 380 (2008).
- G. Falkovich and A. Pumir, “Sling Effect in Collisions of Water Droplets in Turbulent Clouds,” J. Atmos. Sci. 64, 4497 (2007).
- M. S. Paoletti, M. E. Fisher, K. R. Sreenivasan, and D. P. Lathrop, “Velocity Statistics Distinguish Quantum Turbulence from Classical Turbulence,” Phys. Rev. Lett 101, 154501 (2008).
- J. E. Stawarz et al., “Observations of Turbulence in a Kelvin-Helmholtz Event on 8 September 2015 by the Magnetospheric Multiscale Mission,” J. Geophys. Res. Space Phys. 121, 11021 (2016).
- Z.-S. She and E. Leveque, “Universal Scaling Laws in Fully Developed Turbulence,” Phys. Rev. Lett. 72, 336 (1994).
- C. Rorai, P. D. Mininni, and A. Pouquet, “Turbulence Comes in Bursts in Stably Stratified Flows,” Phys. Rev. E 89, 043002 (2014).