Polymers Reduce Drag More than Expected
Frictional drag steals energy from a moving fluid, but the loss usually becomes greater as the flow goes from smooth, or “laminar,” to turbulent. The onset of turbulence therefore poses a problem for many situations involving fluid flow through a conduit, be it oil in a giant pipeline, blood in a human aorta, or liquid in a heat exchanger. One established solution is to add a small amount of polymer to the fluid, which reduces drag by suppressing turbulence. Decades of experiments, however, have indicated that this approach reduces drag only down to a certain level, known as the maximum drag reduction (MDR) asymptote. Beyond this limit, adding more polymer has no effect. A team led by Björn Hof [1] at the Institute of Science and Technology in Austria has now uncovered a window of flow conditions under which drag can be reduced beyond the usual MDR limit. Their experiments with water and common polymers also offer a new picture of the fluid-dynamical properties associated with MDR.
The drag-reducing effects of polymer in a fluid were discovered by chance. In 1946, B. A. Toms [2] was studying the mechanical degradation of long-chained polymer molecules in water flowing through a pipe. He found that dissolving a minute amount of polymer in the fluid reduced drag up to 70%, even though it had practically no effect on the fluid’s shear viscosity. To this day, the exact mechanism for this drag reduction is obscure. But the leading explanation is that the polymers interact with the flow by stretching and removing energy from the turbulent velocity fluctuations. The polymers' response reduces momentum transport towards the wall and, in turn, drag [3].
Researchers have known since the 1970s [4] that increasing the polymer concentration continues to reduce the drag only up to the MDR asymptote. This limit is “universal” for normal (Newtonian) fluids in the sense that it is generally independent of the type of fluid or polymer additive [4]. But what’s actually happening at MDR has been an open question. In explaining the MDR limit, researchers have tended to focus on the transitional region between laminar and turbulent flow that occurs as the Reynolds number (Re) is increased. (Re is a dimensionless number expressing the ratio between inertial and viscous forces.) In pipes, the laminar-to-turbulent transition for a Newtonian fluid like water usually occurs around Re ∼2000. At this transitional, or “boundary,” point, the flow is unstable, containing pockets of short-lived turbulence. The hypothesis is that adding polymer to a fluid pushes the transitional Re to a higher value. But once MDR is reached, adding more polymer does nothing because the flow is supposedly “trapped” in the boundary state (see Refs. [3, 5]). Whether this MDR boundary state corresponds to Newtonian turbulence (pockets of turbulence) or some yet unknown type of turbulence is, however, unclear.
A 2013 study by Hof’s group [6] provided a better understanding of the MDR state. Their experiments examined the flow patterns of polymer-containing water at progressively higher Re. They found that when the polymer concentration is small, the transition from laminar to turbulent flow moves to higher Re, just as expected. But when the polymer concentration is moderately high, the transition from laminar to disordered flow occurs at Re values that are below that associated with the transition in pure water. The researchers concluded that this unexpected “early turbulence” is driven by an elastic instability, which appears when polymers are sufficiently stretched by the flow. Under these conditions, a new type of turbulence, dubbed elastoinertial turbulence, can occur in which chaotic flow extends throughout the fluid instead of in pockets. Hof and colleagues therefore proposed that MDR dynamics are associated with elastoinertial turbulence and not with subdued Newtonian turbulence.
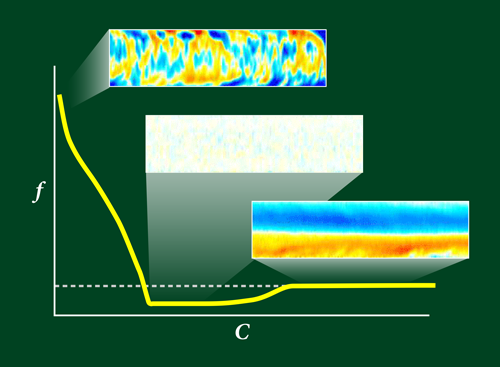
Their new experiments provide more conclusive evidence for this picture [1]. The researchers used the optical technique of particle imaging velocimetry (PIV) to determine the flow patterns of water flowing in a pipe for an extensive range of Re values and polymer concentrations. They then characterized these patterns as laminar (smooth flow), Newtonian turbulent (pockets of turbulence), or elastoinertial turbulent (extended, low-amplitude turbulence). They also determined the amount of drag in terms of a friction factor, which is based on the pressure drop along the pipe. They measured this friction factor at fixed Re and at increasing values of polymer concentration, thus identifying the MDR as the point at which the friction factor flattens out even as concentration increases.
Their PIV maps revealed that the MDR limit results from the interplay between two states of turbulence: Newtonian turbulence, which dominates at low polymer concentration, and elastoinertial turbulence, which dominates at high polymer concentration. Notably, they found that adding the right amount of polymer to water at Re between ∼2000 and ∼3600, where Newtonian turbulence is usually present, relaminarizes the flow completely. In this intermediate, relaminarized phase, the friction factor dips below the MDR asymptote (Fig. 1), which is the first time anyone has witnessed a breaking of this limit. However, adding more polymer induces elastoinertial turbulence, which drives up the friction factor until MDR is reached.
The researchers tested various polymers and found that the drag reduction below MDR occurred in slightly different windows of Re and concentrations. For polyacrylamide, the enhanced drag reduction was observed in water with Re as high as 3600. This Re is compatible with certain medical applications, where, for example, one would want to avoid turbulent blood flow in narrowed arteries (stenosis) [7, 8]. If drag reducing agents could prevent turbulence, that could relieve stress on the heart or prevent damage to blood cells from excessive shear. However, the Re value in many practical situations is much higher than 3600. For example, in oil pipelines, Re >105, so it remains to be seen if polymer additives can be developed for drag reduction there. But the pursuit is well worth the effort, as the difference in friction factor between the turbulent and laminar states in such pipelines is several orders of magnitude. Finding the right additives to make the flow laminar would allow for a tremendous saving in energy costs.
This research is published in Physical Review Letters.
References
- G. H. Choueiri, J. M. Lopez, and B. Hof, “Exceeding the Asymptotic Limit of Polymer Drag Reduction,” Phys. Rev. Lett. 120, 124501 (2018).
- B. A. Toms, Proceedings of the International Congress on Rheology, Sec. II (North-Holland, Amsterdam, 1949), p. 135; “Address at the Banquet of the IUTAM Symposium on Structure of Turbulence and Drag Reduction: On the Early Experiments on Drag Reduction by Polymers,” Phys. Fluids 20, S3 (1977).
- I. Procaccia, V. S. L’vov, and R. Benzi, “Colloquium: Theory of Drag Reduction by Polymers in Wall-Bounded Turbulence,” Rev. Mod. Phys. 80, 225 (2008).
- P. S. Virk, H. S. Mickley, and K. A. Smith, “The Ultimate Asymptote and Mean Flow Structure in Toms’ Phenomenon,” J. Appl. Mech. 37, 488 (1970).
- Li Xi and M. D. Graham, “Dynamics on the Laminar-Turbulent Boundary and the Origin of the Maximum Drag Reduction Asymptote,” Phys. Rev. Lett. 108, 028301 (2012).
- D. Samanta, Y. Dubief, M. Holzner, C. Schafer, A. N. Morozov, C. Wagner, and B. Hof, “Elasto-Inertial Turbulence,” Proc. Natl. Acad. Sci. U.S.A. 110, 10557 (2013).
- J. L. Unthank, S. G. Lalka, J. C. Nixon, and A. P. Sawchuk, “Improvement of Flow through Arterial Stenoses by Drag Reducing Agents,” J. Surg. Res. 53, 625 (1992).
- M. V. Kameneva, Z. J. Wu, A. Uraysh, B. Repko, K. N. Litwak, T. R. Billiar, M. P. Fink, R. L. Simmons, B. P. Griffith, and H. S. Borovetz, “Blood Soluble Drag-Reducing Polymers Prevent Lethality from Hemorrhagic Shock in Acute Animal Experiments,” Biorheology 41, 53 (2004), https://content.iospress.com/articles/biorheology/bir288.