The Hunt for No Neutrinos

Jonathan Engel; Petr Vogel

Viewpoint

The Hunt for No Neutrinos

Jonathan Engel

Department of Physics and Astronomy, University of North Carolina, Chapel Hill, NC 27599, USA

Petr Vogel

Kellogg Radiation Laboratory and Physics Department, California Institute of Technology, Pasadena, CA 91125, USA

March 26, 2018• Physics 11, 30

Four experiments have demonstrated new levels of sensitivity to neutrinoless double-beta decay, a process whose existence would prove that neutrinos are their own antiparticles.

Figure caption — **Figure 1:** “Two-neutrino” double-beta decay (left) is allowed in certain isotopes and involves the transformation of two neutrons into two protons, two electrons, and two antineutrinos. If neutrinos are Majorana particles then a neutrinoless form of this double-beta decay should be allowed. Different models for the decay describe it in terms of the creation and destruction of a Majorana neutrino (center) or of an unknown heavier particle (right).

The search for physics beyond the standard model—our current best description of fundamental particles and the interactions between them—is a top priority at high-energy particle accelerators. But researchers are also searching for new physics in the “low-energy” environment of the nucleus through a process known as neutrinoless double-beta ( $0 𝜈 𝛽 𝛽$ ) decay. This hypothetical decay would show that neutrinos are their own antiparticles and that a fundamental law—the conservation of lepton number—is violated in nature. It would also explain why neutrinos are so light. Four experimental collaborations [1–4] are reporting new lower limits on the decay’s half-life, all of which exceed $1 0^{25}$ years. Several of these experiments should reach the $1 0^{26}$ level soon, thus catching up with a fifth experiment [5]. These new results invite a discussion of why detecting $0 𝜈 𝛽 𝛽$ decay is of interest and what physicists might learn as the experiments become more sensitive.

A striking feature of neutrinos is their extremely small mass. The particles, which exist in three possible mass states, are about $1 0^{6}$ times lighter than the next lightest fermion, the electron. This vast discrepancy suggests that the origin of neutrino mass is different from that of all other fermions, involving physics that goes beyond the standard model. Most such extensions of the model say that the neutrinos are Majorana particles—meaning they are their own antiparticles. These theories explain the light neutrino masses as being inversely proportional to a large mass scale set by other particles that have yet to be seen.

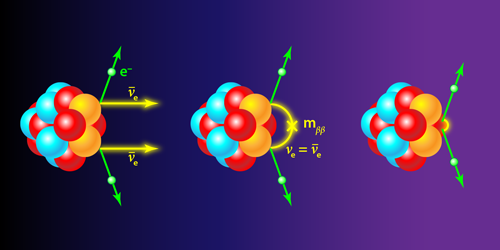
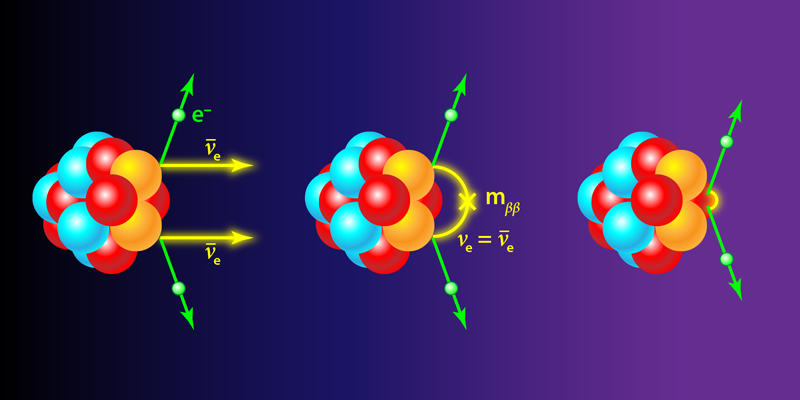
Now if neutrinos are Majorana particles, then they violate the conservation of lepton number—the quantum number that is assigned to all leptons and is $1$ for electrons and neutrinos and $- 1$ for their respective antiparticles. In the process of two-neutrino beta decay (Fig. 1, left), which is allowed in certain isotopes, two neutrons transform into two protons plus two electrons and two antineutrinos. Lepton number is therefore conserved because the electrons and antineutrinos have opposite lepton number. But if neutrinos are Majorana particles, double-beta decay can occur without the emission of antineutrinos, meaning the lepton number changes by $2$ .

Various mechanisms for this neutrinoless process are possible. They involve the creation and destruction of either a virtual Majorana neutrino (Fig. 1, center) or of some new heavy particle (Fig. 1, right). If nature chooses the first scenario (virtual Majorana neutrinos), the decay rate is proportional to the square of a mass called $m_{𝛽 𝛽}$ , which is a weighted average of the masses of the three neutrino mass states. If nature prefers the second option (heavy particles), the relation between the decay rate and neutrino masses is more complicated. But detecting the decay, no matter which mechanism causes it, would tell us that neutrinos are Majorana particles and that there are new particles allowing the nonconservation of lepton number. The discovery that lepton number isn’t conserved might also point physicists toward an explanation for the observed asymmetry between matter and antimatter.

The four experiments all determine the decay half-life (the inverse of the decay rate) in roughly the same way: by monitoring a large number of atoms of a given double-beta decay isotope and looking for a peak in the two-electron energy. (In $0 𝜈 𝛽 𝛽$ decay, the two electrons carry away all of the decay energy, which is the mass difference between the initial and final nucleus.) Where the experiments differ is in which isotope they use and how they measure the electron energies. GERDA [1], located at Italy’s Gran Sasso underground laboratory, and the MAJORANA Demonstrator [2], at the US’s Sanford Underground Research Facility, both look for the decays in materials enriched with germanium-76. EXO-200 [4], at the Waste Isolation Pilot Plant in the US, analyzes liquid xenon enriched with xenon-136. Finally, CUORE [3], also located at Gran Sasso, studies ${TeO}_{2}$ crystals made of natural tellurium, 34% of which is the double-beta decay isotope tellurium-130.

To date, the best limits on the half-life come from GERDA, which today reports a lower limit of $8 \times 1 0^{25}$ years [1] and from a fifth experiment, KamLAND-Zen, at the Kamioka Observatory in Japan, which uses xenon-136 and achieved a limit of $1.07 \times 1 0^{26}$ years in 2016 [5]. The limits reported last month by EXO-200 ( $1.8 \times 1 0^{25}$ years [4]), and today by MAJORANA ( $1.9 \times 1 0^{25}$ years [2]) and by CUORE ( $1.3 \times 1 0^{25}$ years [3]) are close.

Why choose one isotope over another? The expected decay rate for a given isotope depends on the nuclear wave function and the density of final electron states. The heavier isotopes (xenon-136 and tellurium-130) offer a sixfold enhancement of the electron-state density compared with germanium-76. But the contribution from the nuclear wave function is expected to be greatest in germanium-76 [6]. When all is said and done, the three isotopes offer nearly equivalent sensitivity to $m_{𝛽 𝛽}$ or the physics of heavy new particles, with perhaps a slight advantage to the heavier two.

Ultimately, the most important ingredient in sensitivity is exposure, the product of the amount of active isotope and the measuring time. But another crucial element is the ability to recognize a feeble electron peak in a sea of background. To eliminate “false” counts, the experiments typically narrow the search to energies in a small region of interest near the decay energy. The better the energy resolution of a detector, the more false counts it can exclude. The CUORE experiment has more exposure than either of the germanium experiments, but its resolution is not as high. As a result, the half-life limit from GERDA, which (like MAJORANA) has created “zero-background” conditions in its region of interest, is somewhat higher than that from CUORE. The xenon experiments have the largest exposure of all but the poorest resolution. That’s why they have so far provided comparable limits to those from the germanium experiments.

With higher sensitivities, the experiments could start to have a significant chance of actually discovering $0 𝜈 𝛽 𝛽$ decay. Constraints on $m_{𝛽 𝛽}$ from other experiments suggest that it could be larger than 10 meV. If it is as large as 50 meV, and assuming the decay is mediated by virtual Majorana neutrinos, then estimates [6] suggest that a detection is possible with an experimental sensitivity of $5$ – $8 \times 1 0^{26}$ years. But if $m_{𝛽 𝛽}$ is closer to 10 meV, then a much higher sensitivity of $1$ – $2 \times 1 0^{28}$ years will be needed to see the decay. The first of these goals might be achieved by some of the experiments if they simply continue to run. But the detectors will need a roughly 100-fold improvement in sensitivity to reach the second goal, a boost that requires a ton or more of active material and better techniques to eliminate background. (See, for example, the 26 March 2018 Focus story.) Zero-background experiments offer the best scaling in sensitivity with increasing exposure. But reaching zero background with tons of material will be a technical challenge, requiring significant funding.

Collaborations have already formed to build larger detectors with all three isotopes. But do we need so many experiments dedicated to the same measurement when one isn’t obviously better than the other? The first answer is that detecting the decay would require a rewriting of textbooks—lepton number is not conserved and neutrinos are Majorana—so having complementary experiments is essential to confirm such a major result. But there’s another reason to have multiple projects. If we detect the decay, we want to understand more about it. Is it driven by light or heavy particles? If the latter, what are the properties of the new particles? These questions are easier to answer if we can measure the decay rates in more than one isotope. In addition, a more definitive understanding of the mechanism for lepton number violation would come from measuring the single-electron energy spectrum and other details of the decay. Having a suite of experiments dedicated to the same problem will help researchers decide how best to conduct these more challenging measurements.

This research is published in Physical Review Letters.

Correction (26 March 2018): This article has been revised to clarify that the tellurium-130 used in the CUORE experiment is naturally occurring.

References

M. Agostini et al. (GERDA Collaboration), “Improved Limit on Neutrinoless Double- $𝛽$ decay of $^{76} Ge$ from GERDA Phase II,” Phys. Rev. Lett. 120, 132503 (2018).
C. E. Aalseth et al. (MAJORANA Collaboration), “Search for Neutrinoless Double- $𝛽$ decay in $^{76} Ge$ with the Majorana Demonstrator,” Phys. Rev. Lett. 120, 132502 (2018).
C. Alduino et al. (CUORE Collaboration), “First Results from CUORE: A Search for Lepton Number Violation via $0 𝜈 𝛽 𝛽$ decay of $^{130} Te$ ,” Phys. Rev. Lett. 120, 132501 (2018).
J. B. Albert et al. (EXO-200 Collaboration), “Search for Neutrinoless Double-Beta Decay with the Upgraded EXO-200 Detector,” Phys. Rev. Lett. 120, 072701 (2018).
A. Gando et al. (KamLAND-Zen Collaboration), “Search for Majorana Neutrinos Near the Inverted Mass Hierarchy Region with KamLAND-Zen,” Phys. Rev. Lett. 117, 082503 (2016).
J. Engel and J. Menéndez, “Status and Future of Nuclear Matrix Elements for Neutrinoless Double-Beta Decay: A Review,” Rep. Prog. Phys. 80, 046301 (2017).

About the Authors

Jonathan Engel is a professor at the University of North Carolina, Chapel Hill. He received his Ph.D. from Yale in 1986 and pursued postdoctoral research at both the California Institute of Technology, where he worked with Petr Vogel, and at the Bartol Research Institute of the University of Delaware. He has a longstanding interest in tests of fundamental physics in nuclei. He is currently the principal investigator of the Department of Energy’s Topical Nuclear Theory Collaboration for Double-Beta Decay and Fundamental Symmetries. In 2014 he was recognized as an Outstanding Referee by the American Physical Society.

Petr Vogel is an Emeritus Senior Research Associate at the Kellogg Laboratory of the California Institute of Technology (Caltech). He received his undergraduate degree from Charles University in the Czech Republic and from the Czech Institute of Technology, Prague. He completed his Ph.D. in nuclear theory at the Joint Institute of Nuclear Research in Russia. He joined Caltech in 1970. His research interests involve nuclear structure theory, nuclear reactor neutrinos, and double-beta decay theory. In 2008 he was recognized as an Outstanding Referee by the American Physical Society.