Watching a Quantum Magnet Grow in Ultracold Atoms
The idea that matter can organize into distinct phases is simultaneously familiar and profound. Phases of matter can be as mundane as liquid water and solid ice or as exotic as Bose-Einstein condensates and superfluids. Phase transitions are even invoked in beyond-standard-model cosmology to explain the splitting of the electromagnetic and weak forces a mere picosecond after the big bang. Watching the formation of a phase of matter in real time could shed light on the complex physics that controls phase transitions, but it’s very hard to do experimentally. Two independent experiments—one by Elmer Guardado-Sanchez and co-workers at Princeton University, New Jersey [1], and the other by Vincent Lienhard of the National Center for Scientific Research (CNRS) and Paris-Saclay University, France, and co-workers [2]—have now watched, with atomic detail, how an antiferromagnetic phase of matter begins to form (Fig. 1). The experimental platforms used by the authors are some of the most advanced examples of quantum simulators—types of quantum computers proposed by Richard Feynman in 1982 [3].
To describe what a quantum simulator is, I will first have to disclose a fact that is particularly painful for us theoretical physicists: we can rarely predict the behavior of quantum systems when more than a few particles are interacting. This is not a consequence of limited mathematical prowess or computing power but of the fundamental difficulty of solving quantum mechanics with classical machines. The aim of a quantum simulator is to bypass the need for theoretical calculations—if you want to know the underlying properties of a certain quantum system, then build another more controllable quantum system that is described by the same model and measure its properties.
The two groups have demonstrated potent quantum simulation platforms that use ultracold Rydberg atoms to simulate ensembles of spins. Building on previous work (see, for example, Refs. [4–9]), the researchers engineered setups that can emulate the famous quantum Ising model, which describes mutually interacting spins arranged in a lattice. The Ising model is widely used as a prototypical system for magnetism. It is simple to write down, and it displays phases and phase transitions that are observed in magnetic materials. With the exception of a few simple cases, however, the model cannot be solved, even numerically. Quantum simulators are a promising way to circumvent such difficulties.
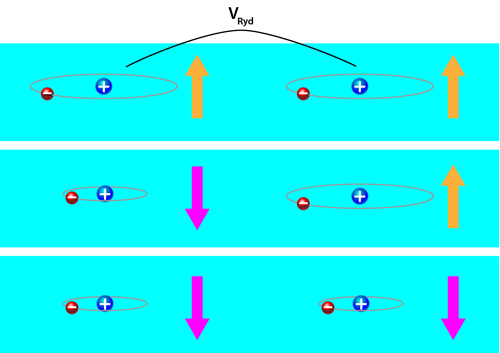
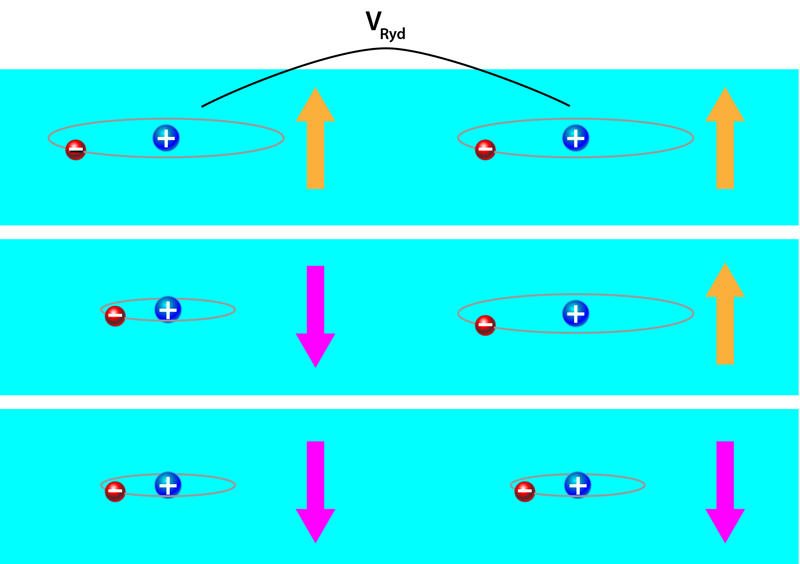
To model the two possible states (up and down) of each individual spin, the new schemes use two internal states of an atom: the electronic ground state and a Rydberg state (Fig. 2). A Rydberg state is an excited state in which one electron orbits far from the nucleus, corresponding to a very high principal quantum number n . In the experiments of Guardado-Sanchez et al. and Lienhard et al., the Rydberg states have n=23 and n=64, respectively. Rydberg states offer two useful properties: they are longer lived than other excited states, and the interactions between neighboring atoms in the Rydberg state are enhanced by many orders of magnitude compared to those between atoms in the ground state. Such Rydberg interactions can mimic the interactions between spins (Fig. 2).
Both experiments use lasers to trap the atoms in lattice potentials, but the lattices have different geometric layouts. Guardado-Sanchez et al. use the standing waves created by interfering lasers to make a two-dimensional square grid that can contain over 200 atoms. Lienhard et al. use tightly focused lasers to trap up to 36 atoms in a fully controllable configuration, with which they realize a ring, a square lattice, and a triangular lattice.
The researchers tune the conditions of their experiment to simulate antiferromagnetic Ising models. Lienhard et al. use repulsive interactions between atoms in the Rydberg state to mimic an antiferromagnetic interaction, which favors antialigned spins. Guardado-Sanchez et al. use attractive Rydberg interactions, which would normally mimic an alignment-favoring ferromagnetic interaction. However, they exploit a clever trick: they study the high-energy states of a system with ferromagnetic interactions, which are well known to correspond to the low-energy states of an antiferromagnetic system.
Using their quantum simulators, the two groups study the growth of an antiferromagnetic phase. They start by preparing a paramagnetic phase in which all spins point down in a strong “simulated” magnetic field. (The field is simulated using lasers that couple the ground and Rydberg states [10].) Then they ramp up the field’s strength to a new value at which the system should have an antiferromagnetic ground state. The experiments reveal that the atomic states gradually rearrange over time so that their spins become antialigned, creating the characteristic checkerboard pattern of an antiferromagnet (Fig. 1).
The formation of an antiferromagnetic phase is expected, since if an atom is in the Rydberg state, its neighbors prefer the ground state and vice versa [11]. The researchers, however, discover interesting phenomena in the dynamics with which antiferromagnetic correlations develop. Both experiments reveal that correlations spread in space at a finite speed, as illustrated in Fig. 1. Lienhard et al. show that such behavior resembles that of a “light cone,” which describes the possible paths that light can take through spacetime [12]. The implication is that correlations—like information in relativity—can propagate only below a fixed speed. (The speed limit for correlations is unrelated to, and usually much slower than, the speed of light.) Lienhard et al. also report a more surprising finding. Unlike for a ring or square lattice, the triangular lattice’s pattern of correlations dynamically reached through the magnetic-field ramp are noticeably different from the lattice’s equilibrium states. They conjecture that this may be because the triangular lattice is “frustrated”: although two neighboring spins in a triangle can antialign, the third spin will not be able to antialign with both of its neighbors simultaneously. Frustration is an important phenomenon in magnetism, as it enhances quantum fluctuations and can lead to exotic phases of matter. The triangular-lattice setup studied by Lienhard and co-workers might help the researchers shed light on the connection between the dynamics of magnets and frustration.
Both experiments also uncover behavior that deviates from that expected for ideal Ising models: the antiferromagnetic correlations saturate at values slightly lower than their expected equilibrium values and then decay with time. The authors suggest that this arises from a form of noise in the system known as decoherence, which disturbs the quantum superpositions of states. In both experiments, decoherence occurs on timescales comparable to those associated with the growth of the antiferromagnet. To fully harness the potential of their quantum simulators, the researchers will have to understand the sources of decoherence and mitigate or adapt to them.
Guardado-Sanchez et al. and Lienhard et al. have watched with unprecedented detail the dynamical process of phase formation in large quantum systems whose underlying Ising models can’t be solved. Together with a handful of other recent demonstrations, these experiments point to a bright future for cold-matter-based quantum simulators. We can expect these simulators to soon have a profound impact on our understanding of many phenomena in quantum magnetism that still defy explanation, such as exotic phases of matter or the process of thermalization in quantum systems.
This research is published in Physical Review X.
References
- E. Guardado-Sanchez, P. T. Brown, D. Mitra, T. Devakul, D. A. Huse, P. Schauss, and W. S. Bakr, “Probing the Quench Dynamics of Antiferromagnetic Correlations in a 2D Quantum Ising Spin System,” Phys. Rev. X 8, 021069 (2018).
- V. Lienhard et al., “Observing the Space- and Time-Dependent Growth of Correlations in Dynamically Tuned Synthetic Ising Models with Antiferromagnetic Interactions,” Phys. Rev. X 8, 021070 (2018).
- R. P. Feynman, “Simulating Physics with Computers,” Int. J. Theor. Phys. 21, 467 (1982).
- K. M. Maller, M. T. Lichtman, T. Xia, Y. Sun, M. J. Piotrowicz, A. W. Carr, L. Isenhower, and M. Saffman, “Rydberg-Blockade Controlled-Not Gate and Entanglement in a Two-Dimensional Array of Neutral-Atom Qubits,” Phys. Rev. A 92, 022336 (2015).
- Y.-Y. Jau, A. M. Hankin, T. Keating, I. H. Deutsch, and G. W. Biedermann, “Entangling Atomic Spins with a Rydberg-Dressed Spin-Flip Blockade,” Nat. Phys. 12, 71 (2015).
- H. Labuhn, D. Barredo, S. Ravets, S. de Léséleuc, T. Macrì, T. Lahaye, and A. Browaeys, “Tunable Two-Dimensional Arrays of Single Rydberg Atoms for Realizing Quantum Ising Models,” Nature 534, 667 (2016).
- P. Schauss, J. Zeiher, T. Fukuhara, S. Hild, M. Cheneau, T. Macri, T. Pohl, I. Bloch, and C. Gross, “Crystallization in Ising Quantum Magnets,” Science 347, 1455 (2015).
- J. Zeiher, J. Choi, A. Rubio-Abadal, T. Pohl, R. van Bijnen, I. Bloch, and C. Gross, “Many-Body Interferometry of a Rydberg-Dressed Spin Lattice,” Phys. Rev. X 7, 041063 (2017).
- H. Bernien et al., “Probing Many-Body Dynamics on a 51-Atom Quantum Simulator,” Nature 551, 579 (2017).
- A laser can mimic both the transverse and longitudinal component of a magnetic field. The transverse component of the magnetic field arises from the laser coupling the ground and Rydberg state, while the longitudinal component is given by the detuning of the laser frequency with respect to the Rydberg–ground-state transition.
- As genuine quantum systems, the atoms are not strictly in patterns of pure Rydberg and ground-state atoms but in quantum superpositions involving both types of states.
- E. H. Lieb and D. W. Robinson, “The Finite Group Velocity of Quantum Spin Systems,” Commun. Math. Phys. 28, 251 (1972).