No Synchronization for Qubits
In the late 1600s, Christiaan Huygens discovered that two pendulum clocks hung from a common support can eventually tick perfectly in phase. Today we know of many cases of one oscillator adjusting its periodic motion to synchronize with another. The long list of examples includes beating hearts, firing neurons [1], blinking fireflies [1], and sloshing clouds of cold atoms [2]. But despite its ubiquity, synchronization does not appear to be possible in the simplest kind of quantum object—the two-level system, or qubit. That’s the conclusion of theorists Alexandre Roulet and Christoph Bruder of the University of Basel, Switzerland, who report that a quantum system must have three or more energy levels in order to synchronize [3]. This fundamental limit could be relevant to experiments or devices that use synchronization to influence the properties of networks of quantum objects, like spins.
Classical synchronization of two or more oscillators has a few basic ingredients. The oscillators need to be weakly coupled together—in the case of the pendulums Huygens studied, the coupling comes from the mechanical response of the common support. Each oscillator must also be able to tick on its own [4]. Human hearts and fireflies satisfy this condition of “self-sustained oscillation” because they have their own internal mechanisms to beat and blink, respectively. Whether a set of oscillating objects will, in fact, synchronize can be determined by finding a solution to the coupled equations of motion for the objects. If synchronization occurs, the variables that describe each object should repeatedly sweep through a closed curve in phase space called a limit cycle. (An example of such variables would be the angle and angular velocity of a pendulum’s bob.) A stable limit cycle is essential to synchronization—if this curve grows or shrinks in time, it shows that the oscillator motion is too sensitive to external perturbations for synchronization to occur.
By comparison with classical synchronization, quantum synchronization is a young subject, and there is still much about the phenomenon that is poorly understood. Yet many of the ideas from classical synchronization carry over to the quantum case. For instance, so-called Wigner or Husimi plots serve as analogs to the phase-space plots of classical oscillators. These plots describe the time evolution of a quantum state and, therefore, provide the necessary information to determine whether a limit cycle exists. The difficulty of studying quantum synchronization lies in the unique features of quantum systems: they are subject to the uncertainty principle [5], and their dynamics can be affected by quantum entanglement. In addition, quantum synchronization exhibits behavior that has no classical counterpart. For example, the quality factor of synchronized quantum oscillators can be enhanced by “squeezing” the driven oscillators, which entails reducing the uncertainty in one oscillator variable at the expense of greater uncertainty in another variable [6].
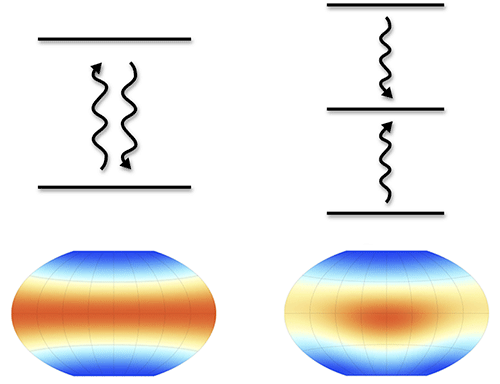
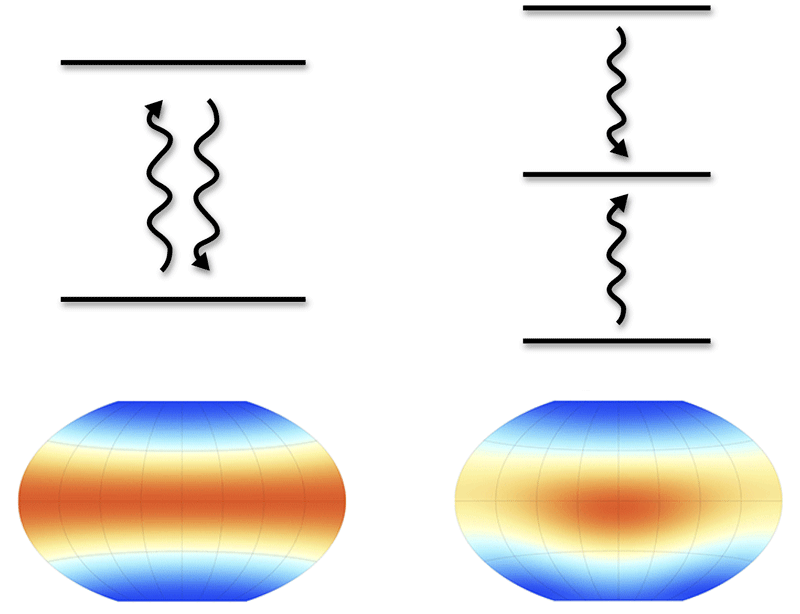
Roulet and Bruder’s study is motivated by the question: Are some quantum systems too simple—or too “small” in a quantum sense—to synchronize? To this end, the researchers consider an arbitrary two-level quantum system, or qubit, that is driven to oscillate between its two levels by an external, oscillating field. Based on a symmetry argument, they conclude that the qubit cannot achieve a limit cycle. This, in turn, rules out the possibility of a qubit synchronizing with another oscillator (Fig. 1, left), since the existence of a limit cycle is the necessary evidence that the oscillator’s dynamics is stable against perturbations. The duo’s finding means that synchronization cannot occur for a spin-1/2 particle.
However, they find that the situation changes for three-level systems, like a spin-1 particle. Such a particle has three distinct states, with Sz=+1, 0 , or −1. The researchers label the state with Sz=0 the target state, and the states with Sz=+1 and −1 are labeled extremal states. They then consider the case of a spin-1 particle that is weakly coupled to a drive field and whose two extremal states could dissipate energy into the target state at particular rates. Based on numerical calculations, they find that the particle will synchronize with the drive when there is a sufficiently large asymmetry between the two dissipation rates (Fig. 1, right).
Roulet and Bruder’s finding recalls a fundamental requirement for lasing: To achieve a population inversion, two levels are not enough, and a third, metastable state is needed. As a future step, it would be interesting to examine the case of multiple interacting oscillators: Two coupled qubits constitute a four-level system, which might be able to synchronize. In addition, Roulet and Bruder were able to determine the degree to which a spin oscillator phase locks with a drive, and further work could determine how this phase locking scales with spin. Their findings raise the question of what other phenomena might operate differently for simple quantum systems. The answer may be relevant to research on quantum entanglement and quantum thermodynamics.
This research is published in Physical Review Letters.
References
- A. Pikovsky, M. Rosenblum, and J. Kurths, Synchronization: A Universal Concept in Nonlinear Sciences, Cambridge Nonlinear Science Series (Cambridge University Press, Cambridge, 2001)[Amazon][WorldCat].
- H. Heimonen, L. C. Kwek, R. Kaiser, and G. Labeyrie, “Synchronization of a Self-Sustained Cold-Atom Oscillator,” Phys. Rev. A 97, 043406 (2018).
- A. Roulet and C. Bruder, “Synchronizing the Smallest Possible System,” Phys. Rev. Lett. 121, 053601 (2018).
- A. A. Andronov, A. A. Vitt, and S. E. Khaykin, Theory of Oscillators (Pergamon Press, Oxford)[Amazon][WorldCat].
- S. Walter, A. Nunnenkamp, and C. Bruder, “Quantum Synchronization of a Driven Self-Sustained Oscillator,” Phys. Rev. Lett. 112, 094102 (2014).
- S. Sonar, M. Hajdušek, M. Mukherjee, R. Fazio, V. Vedral, S. Vinjanampathy, and L.-C. Kwek, “Squeezing Enhances Quantum Synchronization,” Phys. Rev. Lett. 120, 163601 (2018).