Crystals with Defects May Be Good for Spintronics
The active field of spintronics aims to process information using the electron’s spin in place of its charge. So far, the most effective way of manipulating spins electrically has relied on an interaction between an electron’s spin and its motion, known as the spin-orbit coupling. This interaction can be particularly strong in semiconductors, where it has been used to transform an electric current into a current of polarized spins, or a “spin current.” Feng Liu of the University of Utah, Salt Lake City, and colleagues now propose a new way to create the spin-orbit interaction in semiconductors that, compared with the most common approaches, would generate a spin current with a longer-lived polarization [1]. The mechanism in this case relies on a certain kind of crystal defect that can rotate the spins of electrons traveling near it. According to the team’s calculations, this defect-induced spin-orbit coupling could potentially produce coherent, highly polarized spin currents that are useful for spintronics devices.
Spin-orbit coupling in a material occurs when an electron moves through the electric field of surrounding ions, called the crystal field. In the electron’s frame of reference, the crystal field looks like a magnetic field that’s perpendicular to both the electron’s velocity and the crystal field. The electron’s spin, in turn, reduces its energy by aligning with the effective magnetic field—locking the spin’s polarization in a fixed relationship with the electron’s velocity.
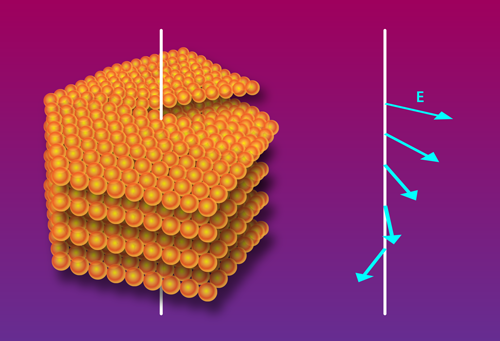
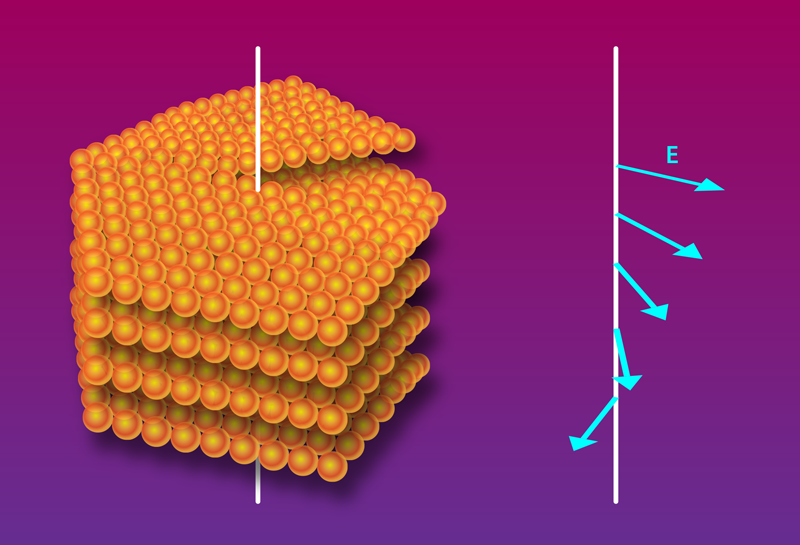
In order for a material to permit spin-orbit coupling, its inversion symmetry must somehow be broken. In the most common types of spin-orbit coupling, this symmetry breaking happens either because the material has an inherently low symmetry (Dresselhaus effect [2]) or because the material is cut off at a surface or interface (Rashba effect [3]). Liu and colleagues’ simple and elegant idea is to achieve the right symmetry conditions with a defect known as a screw dislocation. This topological defect occurs when the atomic planes in a material twist with respect to neighboring planes around an axis [4](Fig. 1). A screw dislocation creates a helicoidal crystalline field, which winds around the axis of the dislocation. Starting from these symmetry considerations, Liu and co-authors analyzed the crystal field of a typical screw dislocation. They then determined an equation that describes the coupling between the components of the electron’s spin and its velocity when the electron is near the defect.
The researchers’ first big finding is that the spin-polarization arising from defect-induced coupling lies in a much narrower range of angles than that resulting from either the Rashba or Dresselhaus effects. The reason has to do with the details of the coupling between velocity and spin. In the Rashba and Dresselhaus effects, there is a one-to-one mapping between an electron’s velocity and its spin polarization[5]. This means that electrons whose velocities are distributed over 360º will have an equivalent distribution of spin orientations. Similarly, if an electron changes direction because it scatters, its spin will change direction too. The mapping between spin and velocity is more restricted for the defect-induced coupling, such that the resulting spin-polarization is confined to 90º. This restriction protects the spin polarization from shifts in electron motion caused by scattering. As a result, the spin polarizations resulting from defect-induced coupling could have a relatively long coherence time.
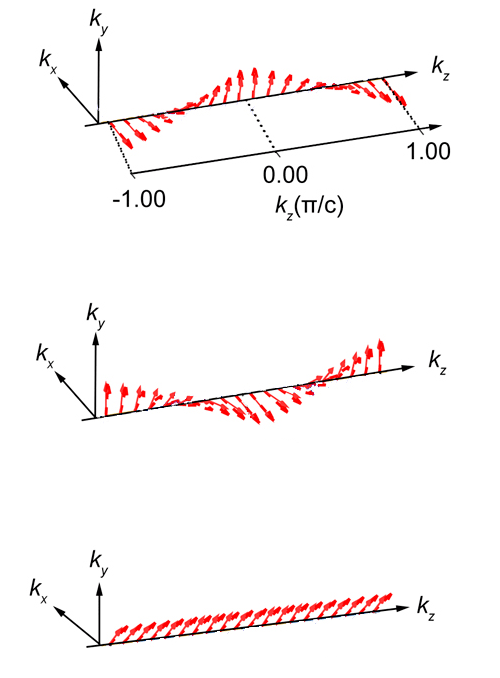
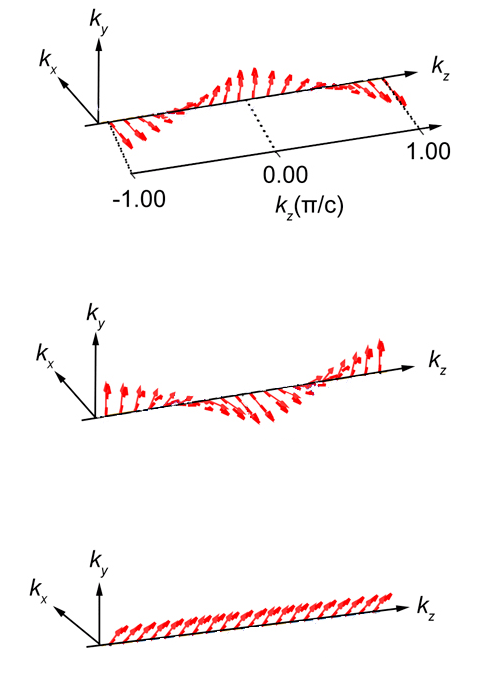
Liu and co-authors gained further insight into the new type of spin-orbit coupling by performing first-principle calculations, such as density-functional theory and tight-binding calculations, on three representative semiconductors: Ge, GaAs, and SiC. For each material, they modeled a single dislocation defect. They found that the form of the crystal field around the defect can be broken into two components—one Rashba-like, the other Dresselhaus-like. In addition, the ratio of these two components depends on the compound’s ionicity, which is a measure of how ionic the atomic bonds are (Fig. 2). Purely Dresselhaus-like spin-orbit coupling occurs in the compound with the weakest ionicity, Ge, while the Rashba-like contribution dominates in the compound with the strongest ionicity, GaAs. Interestingly, the two contributions are equal in SiC, whose ionicity is between that of Ge and GaAs. The Rashba and Dresselhaus contributions rotate spins in opposite directions, so having an equal contribution of the two produces spins with a fixed orientation, a scenario that’s robust against all forms of electron scattering. This finding suggests a way that researchers might engineer a material’s chemistry to achieve the right spin-orbit effect.
The team’s model calculations also reveal that, within a dislocation, all spin-orbit-coupled electrons reside deep in the semiconductor band gap, far from the Fermi level. This feature is important because it would protect the delicate polarization of the spin-orbit-coupled electrons by preventing their hybridization with unpolarized electrons. This result, plus the discovery that ionicity can be used to control the spin orientation, suggests that screw dislocations could provide a unique playground for engineering spin currents with a high degree of coherency.
Dislocations are usually viewed as a nuisance: they can increase electron scattering and alter a material’s mechanical and structural properties. The results from Liu and colleagues change this perspective by giving the defects a useful purpose in material design. Experimentalists who are looking for ways to manipulate and control semiconductor spins will hopefully be inspired to test the predictions. Certainly, the optimal placement and density of the defects, as well as how best to introduce them into a material are all issues that would need to be explored. Future research may also uncover other kinds of defects that yield desirable forms of spin-orbit coupling. Whichever defect they choose, researchers will need to devise clever ways of balancing the good contributions with the bad.
This research is published in Physical Review Letters.
References
- L. Hu et al., “Ubiquitous Spin-Orbit Coupling in a Screw Dislocation with High Spin Coherency,” Phys. Rev. Lett. 121, 066401 (2018).
- G. Dresselhaus, “Spin-Orbit Coupling Effects in Zinc Blende Structures,” Phys. Rev. 100, 580 (1955).
- E. I. Rashba, “Properties of Semiconductors with an Extremum Loop .1. Cyclotron and Combinational Resonance in a Magnetic Field Perpendicular to the Plane of the Loop,” Sov. Phys. Solid. State 1, 1109 (1960).
- F. R. N. Nabarro, Theory of Crystal Dislocations, International Series of Monographs on Physics (Clarendon Press, Oxford, 1967)[Amazon][WorldCat].
- J. Sinova, S. O. Valenzuela, J. Wunderlich, C. H. Back, and T. Jungwirth, “Spin Hall Effects,” Rev. Mod. Phys. 87, 1213 (2015).