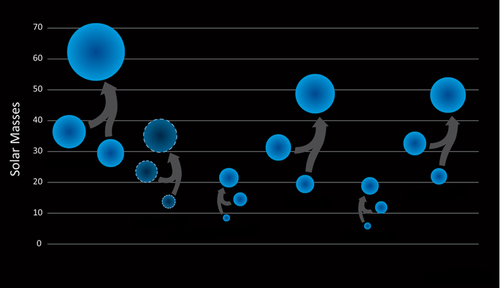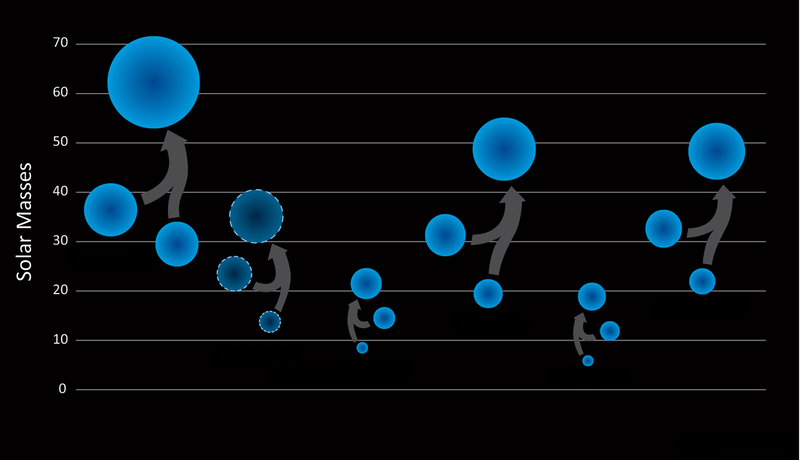Controversy Continues over Black Holes as Dark Matter
Most of the matter in the Universe is dark, and its composition remains a mystery. Among the proposed ingredients, there’s perhaps no darker dark matter candidate than black holes, which could have formed in large numbers in the early Universe. The idea is not new, but it has seen a huge resurgence with the recent gravitational-wave observations of black holes. Support among cosmologists for the black-holes-as-dark-matter hypothesis has been mixed, with some researchers seeing black holes as the cure for a number of outstanding issues in cosmology and others pointing to astronomical observations that constrain black hole numbers. The ongoing debate between these two sides, regardless of its outcome, is pushing researchers to more carefully examine the available data.
The picture that most cosmologists have for dark matter is that it’s some sort of subatomic particle, such as a weakly interacting massive particle (WIMP) or a so-called axion. However, searches for these particles continue to come up empty, opening the door to alternative possibilities. Among the options are black holes, but not the “ordinary” black holes that are known to form when a massive star explodes. To account for the dark matter, cosmologists need a separate population of black holes that formed long before stars. Such “primordial” black holes were first proposed decades ago, but they never garnered a lot of interest, as no hints of their existence were found.
Things changed in 2016, when the LIGO-Virgo collaboration reported the first detection of gravitational waves, and the source was a binary black hole merger (see 11 February 2016 Viewpoint). The sizes of these black holes (around 30 solar masses) were slightly larger—and their rotation rates were slower—than expected from stellar models, so many theorists began considering a primordial origin. “The field has grown dramatically,” says black hole expert Christian Byrnes from the University of Sussex in the UK. “A lot of people now want to get their fingers into gravitational waves and black holes.”
The basic recipe for making primordial black holes is actually pretty simple: all you need is a region in the very early Universe with a density that is roughly twice the average density, and gravity will do the rest. The problem is making the overdense region in the first place: the early Universe appears to have been very uniform—at least on the large scales that astronomers can see by observing the cosmic microwave background (CMB). “If all density fluctuations are as small as those in the CMB, then you wouldn’t produce any black holes in the early Universe,” explains astrophysicist Anne Green from the University of Nottingham in the UK.
However, theorists have devised models of the early Universe that can generate large density fluctuations at small scales, while still matching CMB observations. Juan García-Bellido, a particle physicist from the Autonomous University of Madrid, has one such model, called hybrid inflation [1]. It predicts that the early Universe spat out large numbers of primordial black holes with a wide range of masses. García-Bellido says that these black holes could resolve several open problems in cosmology. For example, the merging of some of these primordial black holes might explain the high numbers of supermassive black holes observed at large distances in x-ray studies. Primordial black holes might also play a role in generating the fluctuations measured in the cosmic infrared background [2].
But of course, the most exciting possibility is that primordial black holes are numerous enough to account for the dark matter. According to García-Bellido’s model, the Milky Way Galaxy should be swimming in a sea of roughly a trillion black holes. “When you tell people that space may be full of black holes, they get nervous,” García-Bellido says. But he adds that the separations are so large that the probability of a black hole coming near our Solar System is very small.
Still, these black holes should occasionally run into things, in particular, each other. The LIGO-Virgo detections of black hole mergers—five so far—are evidence of a large population of black holes in the 10 solar-mass range. But whether or not this population could be large enough to constitute the dark matter is still under debate.
Recent calculations have shown that if dark matter were made up of black holes weighing between 10 and 300 solar masses, then LIGO should have detected hundreds more mergers in its first run [3]. Turning the argument around: multi-solar-mass black holes can only account for about 1% of the dark matter. “But there are caveats,” admits Yacine Ali-Haïmoud from New York University, who helped set those limits. One of these caveats relates to clustering. García-Bellido explains that primordial black holes could form gravitationally-bound groups similar to star clusters. He believes that gravitational perturbations within these groups would lower the overall merger rate, but the full effect of clustering is still a domain of active research [4].
But there are other reasons to question whether black holes are viable contenders for the mantle of dark matter. Researchers have set bounds on how much of the dark matter could be in black holes based on a variety of data, such as CMB observations [5] and stellar density profiles of dwarf galaxies [6]. One of the earliest constraints came from surveys that searched for the temporary brightening of stars that occurs when a black hole passes between a star and Earth—a so-called gravitational lensing effect. A new study of lensing of supernovae claims to rule out black holes weighing more than 0.01 solar masses being a major component of dark matter, subject to some assumptions (see today’s Viewpoint). “There are lots of constraints that together probably exclude black holes with mass around 10 solar masses making up all the dark matter,” Green says. Even so, she calls herself “on the fence,” as there could still be scenarios—such as clustering—that might skirt around the observational bounds.
Many other researchers have come down on one side or the other of that fence. “The community is a bit polarized,” Ali-Haïmoud says. In his mind, it’s too soon to rule in or rule out black holes as dark matter. In fact, the answer may be something in between, with black holes providing some portion of the dark matter and the rest being accounted for by some sort of new particle, he says. “We have no reason to believe that nature was so kind as to only give us one type of dark matter.”
–Michael Schirber
Michael Schirber is a Corresponding Editor for Physics based in Lyon, France.
References
- S. Clesse and J. García-Bellido, “Massive primordial black holes from hybrid inflation as dark matter and the seeds of galaxies,” Phys. Rev. D 92, 123523 (2015).
- A. Kashlinsky, “LIGO gravitational wave detection, primordial black holes and the near-IR cosmic infrared background anisotropies,” Astrophys. J. 823, L25 (2016).
- Y. Ali-Haïmoud, E. D. Kovetz, and M. Kamionkowski, “Merger rate of primordial black-hole binaries,” Phys. Rev. D 96, No. 12 (2017).
- T. Bringmann, P. F. Depta, V. Domcke, and K. Schmidt, “Strong constraints on clustered primordial black holes as dark matter,” arXiv:1808.05910.
- Y. Ali-Haïmoud and M. Kamionkowski, “Cosmic microwave background limits on accreting primordial black holes,” Phys. Rev. D 95, 043534 (2017).
- S. M. Koushiappas and A. Loeb, “Dynamics of dwarf galaxies disfavor stellar-mass black holes as dark matter,” Phys. Rev. Lett. 119, 041102 (2017).