Quantum Correlations Take a New Shape
Bell experiments provide perhaps the clearest demonstration of how radically quantum physics departs from classical physics. In such experiments, pairs of quantum particles are prepared in special entangled states and separately measured. The measurement outcomes are found to be correlated more strongly than allowed by any local, classical theory. The last few decades have seen intense theoretical and experimental efforts to investigate this phenomenon—with the first watertight demonstrations only recently achieved—and to apply it to quantum information. But all that work stuck to the same template used by John Stewart Bell over 50 years ago: two or more particles are jointly prepared by the same source and then independently measured. Now, Marc-Olivier Renou of the University of Geneva and colleagues have broken that mold with the discovery of a new form of quantum correlation arising in a more complex, triangular network of sources and observers [1]. This result offers a tantalizing hint that there may be a whole zoo of nonclassical correlations that are fundamentally different from those identified by Bell.
In 1935, Albert Einstein, Boris Podolsky, and Nathan Rosen (EPR) showed that quantum theory predicted odd correlations in the outcomes of measurements on two distant entangled particles [2]. Making a locality assumption—a measurement on one particle should not have an immediate effect on the state of the other particle—they argued that quantum theory needed to be completed in order to explain these correlations. If this completion could be achieved, quantum correlations wouldn’t be any more mysterious than finding the same stories in different copies of a newspaper. But Bell later showed that experiments might be able to reveal quantum correlations strong enough to rule out such a prosaic explanation [3].
It took a while for this result to be fully appreciated, but a flurry of work eventually followed up on Bell’s insight [4]. On the theoretical side, researchers developed a better mathematical understanding of Bell nonlocality, generalized it to larger numbers of entangled particles, and proposed several cryptographic applications of the phenomenon. On the experimental side, the hard-to-explain correlations were exhibited under ever-stricter conditions, culminating in 2015 with “loophole-free” demonstrations (see 16 December 2015 Viewpoint). These experiments established beyond reasonable doubt that our world cannot be described by any form of classical theory and paved the way for practical applications.
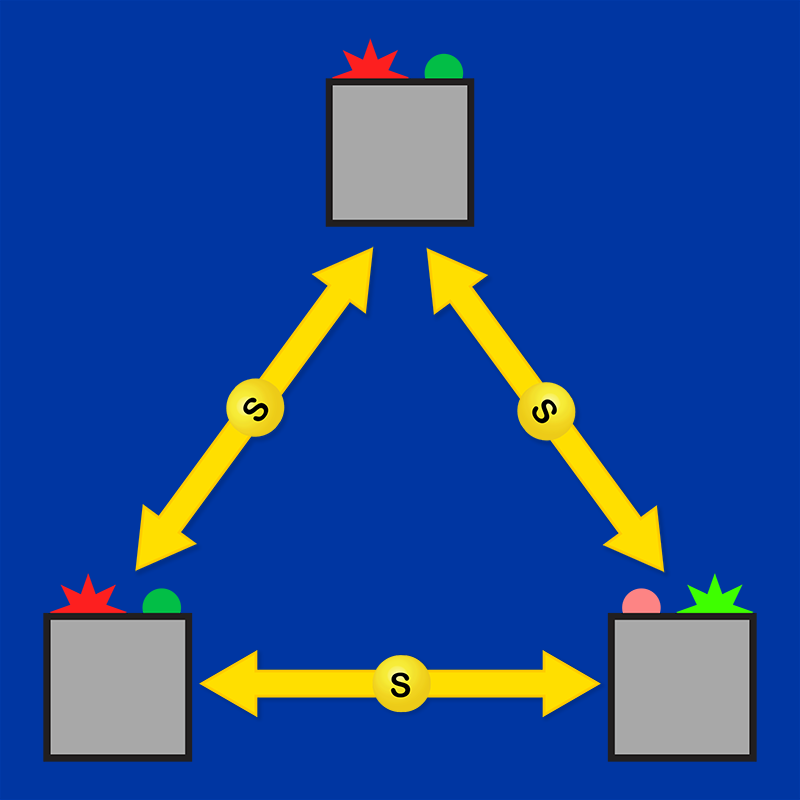
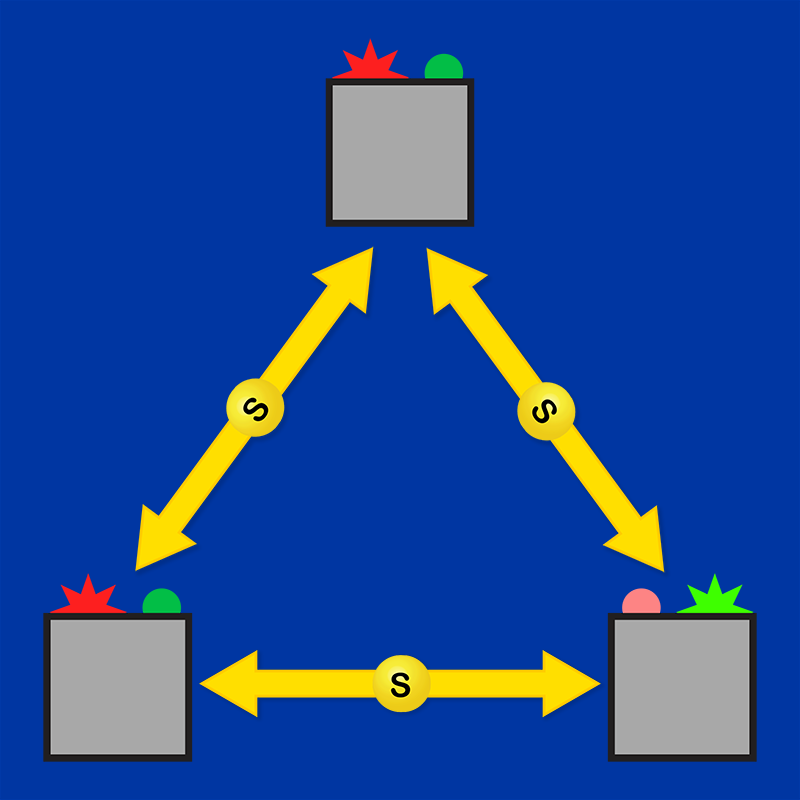
All these studies involved the same “Bell scenario”: one common source prepares entanglement between two or more particles, and observers then perform randomly chosen, independent measurements on each particle. Over the last decade, however, researchers have started to investigate more complex networks of sources and measurements, hunting for new forms of nonclassicality that could possibly lead to quantum information applications. In the “bilocality” scenario [5], for instance, two independent sources share entangled pairs with three observers. This scenario can be used to study entanglement swapping—a way to entangle particles that do not directly interact. Another interesting scenario involves a triangular geometry: three independent sources on the triangle’s sides distribute entangled states to three measurement devices at the triangle’s corners (Fig. 1).
As in the Bell scenario, previous theoretical work showed that both the bilocality [5] and triangle [6] scenarios can lead to quantum correlations much stronger than those achievable classically. However, examples explored for both scenarios were based on careful adaptations of quantum correlations from the Bell scenario. In other words, these examples eventually boiled down to the violation of a standard Bell inequality. Rather than being imported from a Bell scenario, a genuinely new form of nonclassicality should instead be “native” to the new scenario. Researchers haven’t yet found a formal way to prove the nativeness of a new form of correlation. However, there are compelling reasons to believe that the quantum correlations identified by Renou and colleagues are native to the triangle scenario, offering the first example of correlations that are fundamentally different from those of a Bell scenario.
The researchers’ approach was to focus on the triangle scenario and search for the right correlations. They picked the simplest types of quantum particles (two-level qubits) and focused on situations that respected the symmetry of the triangle (Fig. 1): On all edges, three sources send out the same entangled states to the observers, and the observers at the three corners perform the same type of measurement. This assumption reduces the problem to one choice of entangled states and one choice of measurements. Preliminary studies of the triangle scenario had explored obvious candidates for these choices: highly nonclassical states and measurements said to be “maximally entangled.” Alas, it was quickly seen that the quantumness of these states and measurements, when combined in a triangle network, cancel out, leading to correlations that aren’t stronger than classical ones.
An idea to move forward is to keep the same states but explore different measurements. Nicholas Gisin, one of the authors on the new paper, recently proposed a less obvious choice of measurements [7], and his group delivered promising numerical results [8]. But they couldn’t yet prove that the resulting correlations are nonclassical. Renou, Grisin, and colleagues cast the net wider by devising even more intricate measurements built from a combination of quantum and classical ingredients. They were then able to show analytically that resulting correlations display features that aren’t compatible with any classical explanation.
Identifying these novel forms of correlation is only a first step. The nature of chosen states and measurements—inherently linked to the triangle geometry—is a strong hint that the correlations cannot be just an expression of standard Bell nonlocality. But further research is needed to conclusively prove that this is the case. Beyond the Bell scenario, and now the triangle scenario, there are many other scenarios in which new types of quantum correlations may be waiting to be discovered [9]. Just as Bell nonlocality has proven to be a resource for cryptographic tasks—such as quantum key distribution and the generation of certifiably random bits—some of these new forms of quantum correlation could be put to work in new tasks tailored to the new scenarios. It’s hard to predict what these tasks might be, but the new work suggests that the triangle scenario might well be the best place to start looking for them.
This research is published in Physical Review Letters.
References
- M.-O. Renou, E. Bäumer, S. Boreiri, N. Brunner, N. Gisin, and S. Beigi, “Genuine quantum nonlocality in the triangle network,” Phys. Rev. Lett. 123, 140401 (2019).
- A. Einstein, B. Podolsky, and N. Rosen, “Can quantum-mechanical description of physical reality be considered complete?,” Phys. Rev. Lett. 47, 777 (1935).
- J. S. Bell, “On the Einstein Podolsky Rosen paradox,” Physics Physique Fizika 1, 195 (1964).
- N. Brunner, D. Cavalcanti, S. Pironio, V. Scarani, and S. Wehner, “Bell nonlocality,” Rev. Mod. Phys. 86, 419 (2014).
- C. Branciard, N. Gisin, and S. Pironio, “Characterizing the nonlocal correlations created via entanglement swapping,” Phys. Rev. Lett. 104, 170401 (2010).
- T. Fritz, “Beyond Bell's theorem: correlation scenarios,” New J. Phys. 14, 103001 (2012).
- N. Gisin, “Entanglement 25 years after quantum teleportation: Testing joint measurements in quantum networks,” Entropy 21, 325 (2019).
- T. Kriváchy, Y. Cai, D. Cavalcanti, A. Tavakoli, N. Gisin, and N. Brunner, “A neural network oracle for quantum nonlocality problems in networks,” arXiv:1907.10552.
- J. Henson, R. Lal, and M. F Pusey, “Theory-independent limits on correlations from generalized Bayesian networks,” New J. Phys. 16, 113043 (2014).