A Quasicrystal for Quantum Simulations
Solids have traditionally been divided into two opposing types: crystals, where the atoms form a long-range periodic pattern, and amorphous materials, where no long-range order of the atoms occurs at all. Somewhere in between are quasicrystals, which lack periodicity yet still display a form of long-range order. To understand this order-disorder frontier, researchers have studied both electrons in quasicrystalline solids, as well as atoms and photons in “synthetic” quasicrystalline lattices. A group led by Ulrich Schneider at the University of Cambridge, UK, has now introduced a new system into the mix—a Bose-Einstein condensate (BEC) of atoms in a 2D quasicrystalline optical lattice [1]. Optical lattices are defect-free and may be engineered more easily than actual crystals, potentially allowing well-controlled simulations of quantum many-body phenomena in a range of new quasicrystal environments.
Mathematically, a periodic structure can have only two-, three-, four-, or sixfold rotational symmetry. But in 1984, Dan Shechtman and collaborators reported their discovery of tenfold rotational symmetry in the electron-diffraction pattern from aluminum-manganese alloys [2]. Although this unusual rotational symmetry couldn’t have come from a crystal, it implied that the atoms in the alloy were ordered in some way. The researchers dubbed the solids quasicrystals, and it was later shown that these strange solids can produce diffraction patterns with other “disallowed” rotational symmetries, including fivefold and eightfold. Shechtman’s pioneering work was recognized with the 2011 Nobel Prize in Chemistry [3].
Quasicrystals have many other features that aren’t found in conventional solids. They are inherently self-similar, like fractals, meaning that patterns in their structure recur as one zooms in and out. This self-similarity can be seen in diffraction patterns, which exhibit peaks at arbitrarily small momenta. In addition, unlike the periodic (Bloch wave) states that exist incrystals, electronic states in quasicrystalline solids have a peculiar fractal structure. Quasicrystals can also be understood as the projection of a higher-dimensional “parent” crystal onto a lower-dimensional space. Studying these materials therefore provides a window into higher-dimensional phenomena [4]. Thirty-five years after their discovery, quasicrystals continue to fascinate researchers [5], and they have been realized in many forms, such as photonic structures [6] and twisted bilayer graphene [7].
An alternative platform for studying quasicrystalline behavior is an atomic gas confined in an optical lattice [8]. Made by interfering two or more laser beams, the typical optical lattice is perfectly periodic. Quasiperiodic lattices can be made by superimposing two lattices whose periodicities are “incommensurate”—meaning their ratio isn’t a rational number. Both 1D and, more recently, 2D quasiperiodic lattices have been produced in this way, but such lattices did not exhibit the forbidden rotational symmetries of a true quasicrystal [9]. A 1997 study succeeded in observing these features with an atom gas in a quasicrystalline optical lattice [10]. But the proximity of the laser frequency to an internal atomic resonance resulted in strong atom-light scattering, which prevented the simulation of quantum many-body behavior.
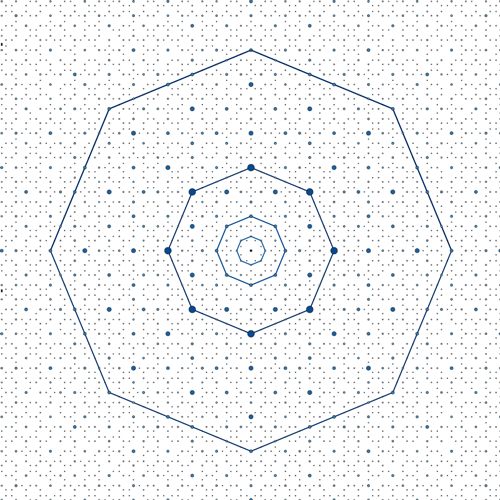
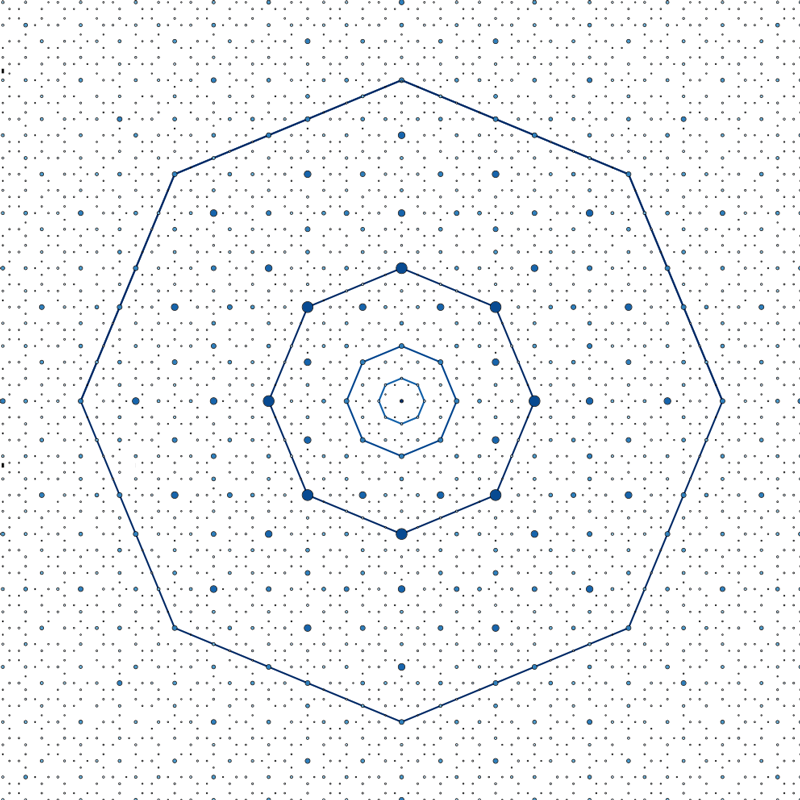
In their new work [1], Schneider and collaborators opened a window into this physics. For one, they realized a 2D quasicrystal optical lattice tuned far from any internal atomic resonance, reducing problematic atom-light scattering effects. They also probed this lattice with a BEC, in which all of the atoms are in the same quantum state. They produced the lattice using a planar arrangement of four intersecting 1D optical lattices, with an angle of 45° between each lattice. By tuning the relative strength of each laser, the team could switch between 1D and 2D periodic potentials, and they could create 2D quasicrystals with eightfold rotational symmetry. In the experiment, the optical lattice was flashed “on” for a few microseconds in the same spot as a preformed BEC of potassium atoms. Over the course of this pulse, the researchers observed a series of momentum states emerging in the BEC as the atoms scattered photons from one of the beams of the lattice into another. Organized in a plot, these states formed a self-similar pattern analogous to the diffraction patterns measured by Shechtman et al. 35 years ago [2]. The new pattern could be described as an infinite sequence of progressively larger octagons (Fig. 1).
Schneider’s team also showed that the time evolution of the BEC on the quasicrystal is quite distinct from that on a periodic lattice. In the quasicrystal, the fractal pattern of momentum states emerges as the atoms move to successively lower and more closely spaced momentum states through a sequence of small, photon-induced velocity kicks. The successive population of these smaller momentum states constitutes a quantum walk in the quasicrystal’s momentum space. But in a periodic lattice, these smaller momentum states are inaccessible.
In the present work, Schneider and colleagues interpret their 2D quasicrystal as an incommensurate projection of a 4D cubic lattice onto a 2D plane. The 4D character of this “parent” lattice is reflected in the properties of the BEC quantum walk, which demonstrates the potential of quasicrystalline optical lattices for simulating higher dimensions. Interesting possibilities include the exploration of the quantum Hall effect and other topological properties in 4D, where exotic new phenomena are expected.
Where else might these experiments lead? One avenue might be the study of a weakly interacting BEC in a quasicrystal, a system whose dynamics is expected to present hybrid features of disorder and periodicity. Another direction would be the investigation of strongly correlated behavior—like that described by Hubbard and spin models—in a quasicrystalline environment. With sufficiently deep potentials, one would realize these models with locally variable parameters and explore such behaviors as antiferromagnetism, Mott transitions, and Bose glass phases in the peculiar setting of a quasicrystal. In addition, the new platform might also provide alternative ways of studying the effects of quasiperiodicity on transport, such as anomalous diffusion and many-body localization.
This research is published in Physical Review Letters.
References
- K. Viebahn, M. Sbroscia, E. Carter, J.-C. Yu, and U. Schneider, “Matter-wave diffraction from a quasicrystalline optical lattice,” Phys. Rev. Lett. 122, 110404 (2019).
- D. Shechtman, I. Blech, D. Gratias, and J. W. Cahn, “Metallic phase with long-range orientational order and no translational symmetry,” Phys. Rev. Lett. 53, 1951 (1984).
- D. Levine and P. J. Steinhardt, “Quasicrystals: A new class of ordered structures,” Phys. Rev. Lett. 53, 2477 (1984).
- J. E. S. Socolar, T. C. Lubensky, and P. J. Steinhardt, “Phonons, phasons, and dislocations in quasicrystals,” Phys. Rev. B 34, 3345 (1986).
- W. Steurer, “Quasicrystals: What do we know? What do we want to know? What can we know?,” Acta Crystallogr. Sect. A 74, 1 (2018).
- B. Freedman, G. Bartal, M. Segev, R. Lifshitz, D. N. Christodoulides, and J. W. Fleischer, “Wave and defect dynamics in nonlinear photonic quasicrystals,” Nature 440, 1166 (2006).
- S. J. Ahn et al., “Dirac electrons in a dodecagonal graphene quasicrystal,” Science 361, 782 (2018).
- I. Bloch, J. Dalibard, and W. Zwerger, “Many-body physics with ultracold gases,” Rev. Mod. Phys. 80, 885 (2008).
- G. Roati, C. D’Errico, L. Fallani, M. Fattori, C. Fort, M. Zaccanti, G. Modugno, M. Modugno, and M. Inguscio, “Anderson localization of a non-interacting Bose–Einstein condensate,” Nature 453, 895 (2008).
- L. Guidoni, C. Triché, P. Verkerk, and G. Grynberg, “Quasiperiodic optical lattices,” Phys. Rev. Lett. 79, 3363 (1997).