3D Map of a Quantum Dot’s Potential
An electron bound to a quantum dot is a conceptually simple implementation of a quantum bit (qubit), with the electron’s spin providing the qubit’s two levels, which encode information [1, 2]. To control electron spin, researchers apply some perturbation to the electron, which rotates the spin to a desired direction. This process is easier when the electron’s location and wave function are known—parameters determinable from the dot’s confining potential. But in quantum dots, researchers often lack this information [1]. Now Leon Camenzind at the University of Basel, Switzerland, and colleagues demonstrate a technique to measure the potential binding an electron in a gallium arsenide (GaAs) quantum dot [3, 4]. Their technique could potentially be used to characterize the confining potential of other systems, providing information that could allow optimization of the efficiency and performance of these systems in quantum devices.
A quantum dot acts like an artificial atom, creating a potential that confines the electron in three dimensions. The electron’s motion is limited to a region determined by the dot’s potential. For an unperturbed quantum dot, the electron’s location and wave function can be determined if the dot’s potential is known. Having this information makes it easier to manipulate the qubit, as researchers can precisely determine the electric or magnetic field they need to force the qubit to evolve into a particular state to perform some desired operation. These manipulations might involve rotating the spin or bringing two spins together so that they interact [1, 2]. Knowing the confining potential and, in turn, the electron’s wave function also allows the time-evolution of the qubit’s state to be obtained, enabling perturbations to be more accurately established and applied.
The commonly used quantum-dot model assumes that the confining potential of the dot matches that of a harmonic oscillator or some closely related expression [1]. But that isn’t always the case. Camenzind and colleagues now demonstrate an ingenious technique for determining the potential confining the electron [3, 4].
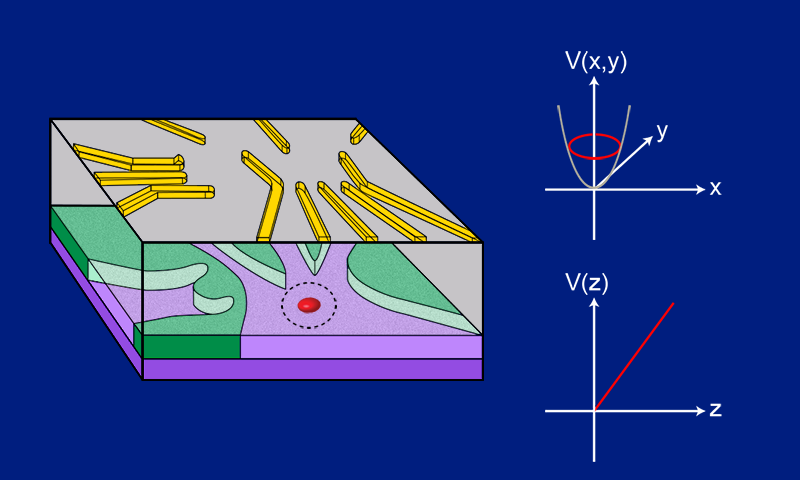
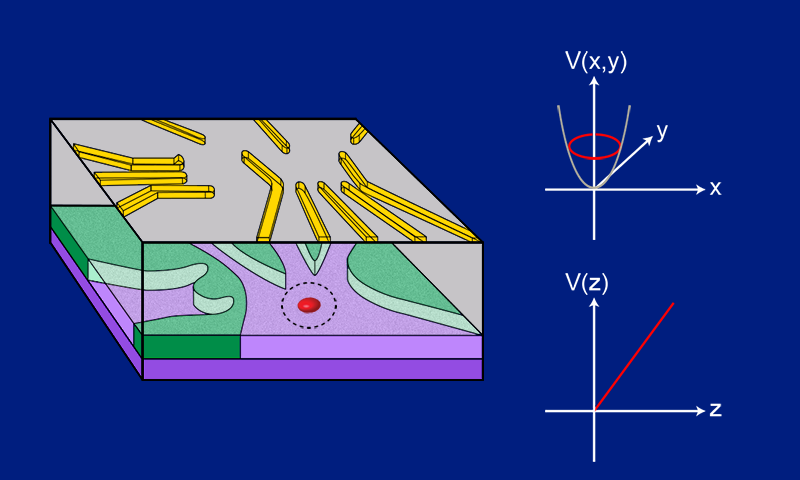
For the demonstration, the team made single-electron quantum dots using gated GaAs/aluminum gallium arsenside (AlGaAs) heterostructures, which consisted of an undoped GaAs layer and then a doped AlGaAs layer (Fig. 1). Electrons from the doped AlGaAs layer diffused toward the GaAs layer and accumulated on the GaAs side of the interface between the two materials. There they formed a two-dimensional electron gas (2DEG)—a “slab” of electrons that are free to move in the x-y plane but tightly confined in the z direction. To define the dots, the team applied voltages to metal gates placed on the surface of the device, which generated electric fields in the 2DEG. The fields create a repulsive potential over a small region of the 2DEG that has an attractive spot at its center, confining a few electrons in the x-y plane to zero dimensions (a quantum dot). Under the right conditions, the number of electrons in the dot is limited to one.
To determine the confining potential, the team applied magnetic fields to the system. The experiments were carried out in two stages. First the team applied magnetic fields of varying strength in the x and then y directions. These fields reduced the width of the confining potential in the y and x directions, respectively, changing the electron’s energy. Using pulsed gate spectroscopy, the team then measured the orbital energy of the electron as a function of magnetic field intensity and compared those energies to those theoretically predicted for different dot confining potentials. From these data, they inferred the shape of the dot in the x-y plane. Then they repeated the measurements, but this time they kept the magnitude of the field fixed while varying its angle. From these measurements, they determined the width of the potential in the z direction. Their results show that the confining potential of their quantum dots had an elongated, deformed circular shape in the x-y plane and a confinement width of around 6 nm in the z direction (Fig. 1).
The analysis method employed by the team required that they make an initial guess for the confining potential, which they then used to make predictions that they compared with the experimental data. In this case, the team guessed that the potential was anisotropic, with independent harmonic shapes in x and y, and that it extended with a triangular shape in the z direction. The need to guess the potential could be interpreted as a limitation of the proposed method. Another potential issue is that different z-direction confining profiles, such as triangular wells and square wells, produce very similar spectroscopic data, making it hard to determine a dot’s exact potential. That said, the method does provide a route to tackling a difficult problem using realistic assumptions. It also provides a means to extract a large amount of information about the dots from a conceptually simple model and a well-defined sequence of measurements. For example, as well as obtaining the 3D shape of the potential, the team was able to measure and to calculate the ground- and excited-state energies for dots with different potential shapes. They were also able to measure the orientation of the dot relative to the underlying GaAs layer.
The work by Camenzind and colleagues represents significant progress toward single-electron control in quantum dots. The team notes that their method should be directly applicable to quantum dots made from other materials, such as silicon/silicon oxide heterostructures [5], as well as multiple-quantum-dot systems, for example a triple quantum dot. The next step will likely be the mapping of a double quantum dot, which should provide insights into the effect of combining two dot potentials [6]. Researchers are in a better position to model a quantum-dot-like qubit if they know its potential, which can be optimized to improve the qubit’s performance and efficiency as it carries out calculations or stores information.
This research is published in Physical Review Letters and Physical Review B.
References
- D. Loss and D. P. DiVincenzo, “Quantum computation with quantum dots,” Phys. Rev. A 57, 120 (1998).
- B. E. Kane, “A silicon-based nuclear spin quantum computer,” Nature 393, 133 (1998).
- L. C. Camenzind, L. Yu, P. Stano, Zimmerman, A. C. Gossard, D. Loss, and D. M. Zumbühl, “Spectroscopy of quantum dot orbitals with in-plane magnetic fields,” Phys. Rev. Lett. 122, 207701 (2019).
- P. Stano, C.-H. Hsu, L. C. Camenzind, L. Yu, Dominik Zumbühl, and D. Loss, “Orbital effects of a strong in-plane magnetic field on a gate-defined quantum dot,” Phys. Rev. B 99, 085308 (2019).
- J. J. Pla, K. Y. Tan, J. P. Dehollain, W. H. Lim, J. J. L. Morton, D. N. Jamieson, A. S. Dzurak, and A. Morello, “A single-atom electron spin qubit in silicon,” Nature 489, 541 (2012).
- F. H. L. Koppens, C. Buizert, K. J. Tielrooij, I. T. Vink, K. C. Nowack, T. Meunier, L. P. Kouwenhoven, and L. M. K. Vandersypen, “Driven coherent oscillations of a single electron spin in a quantum dot,” Nature 442, 766 (2006).