Two-Dimensional Electrons Raise Eyebrows by Pairing Incoherently
Insulators, metals, and superconductors differ in their response to an applied electric field. No electrical charge flows in an insulator. In a superconductor, a supercurrent flows without resistance and cancels the applied field. Only metals tolerate the simultaneous presence of an electric field and a dissipative current flow. These three distinct behaviors are hallmarks of the electrons’ organization in materials—they are attached to atoms in an insulator, they form a condensate of coherent Cooper pairs in a superconductor, and they are free and mobile in metals. There is a long-held belief, however, that confining electrons to 2D would deprive them of the metallic option at zero temperature. In a Colloquium article for Reviews of Modern Physics, a trio of physicists now challenge this view. They identify a fundamental flaw in our assumptions about electron organization in 2D materials [1]. Based on a body of published data and on theoretical arguments, the researchers show that in these materials an unexpected and anomalous form of metallicity can exist at low temperatures at the transition between an insulator and a superconductor.
Four decades ago, theorists argued that noninteracting electrons in 2D could not avoid interfering with each other [2]. This implies that even an infinitesimal degree of disorder—the imperfections in the material—would lead to localization and to insulating behavior. In agreement with this picture, experiments found that many 2D solids are either insulating or superconducting, depending on the strength of an applied magnetic field or the amount of disorder. Using the magnetic field or disorder as tuning knobs, experimental studies have extensively documented transitions between the two states at low temperatures. Approaching this transition from the insulating side, these studies typically saw fluctuations of the superconducting phase growing larger in size and lasting longer in time, indicating a quantum critical point—a continuous phase transition at zero temperature.
However, some of the early data from the 1990s revealed what appeared to be a metallic phase sandwiched between the insulating and superconducting phases [3]. These findings did not, however, attract much attention. The theoretical arguments for localization in 2D remained strong. And there was some debate about how to interpret the data. The signature of a metal is that its conductivity rises with decreasing temperature. But at the low temperatures required to fully examine this property—typically a few thousandths of a degree above absolute zero—it can be tricky to reliably control the electron temperature. The difficulty arises because at these temperatures, electrons thermally decouple from the surrounding lattice. So when electrons heat up by capturing ambient electromagnetic radiation, they cannot easily cool back down, which leaves them warmer than measurements suggest and causes the conductivity to stop rising at low temperatures. Recently, careful experiments have shown that the temperature below which the conductivity saturates because of this effect can be extremely sensitive to the presence of ambient electromagnetic radiation [4].
Aharon Kapitulnik and Steven Kivelson of Stanford University, California, and Boris Spivak of the University of Washington, Seattle, now demonstrate that the evidence for a dissipative metallic state in 2D materials is robust [1]. They collect a large body of published electrical transport data on a variety of 2D superconductors, and they show that all the surveyed materials, despite their specificities, display a similar metallic conductivity at low temperature. This metallicity occurs as the material is made to pass from an insulating phase to a superconducting phase using magnetic field, disorder, or electron density as control parameters. Here the low-temperature conductivity levels off at some saturation value. In some cases, this conductivity saturation persists to temperatures as high as 10 K [5], ruling out the possibility that the saturation is simply caused by uncontrolled ambient radiation.
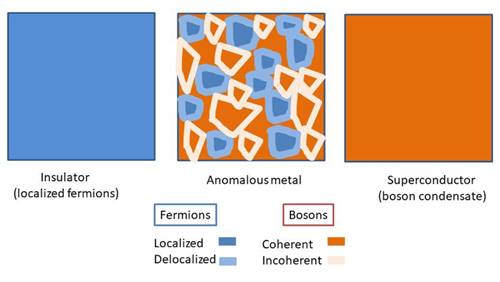
Conceptually, the authors identify this 2D metallic state as a “failed” superconductor, in which electric charge is mostly transported by short-lived Cooper pairs. This identification is motivated by two puzzling features of the observed residual conductivity. The first is that this conductivity is always much larger than expected based on the density of electrons and their mobility. The second is that the conductivity is easily suppressed by a magnetic field, which is unexpected for the fairly disordered materials considered here. These features imply that highly conductive and field-sensitive electrical carriers must be present down to zero temperature, which is naturally explained by invoking short-lived Cooper pairs. However, this state would be a “failed” superconductor since the Cooper pairs would lack the coherence of an actual superconductor.
Kapitulnik, Kivelson, and Spivak’s picture, however, comes with its challenges. The conduction by short-lived Cooper pairs in the normal state of a superconductor, known as paraconductivity, is both theoretically understood and experimentally established [6]. But it’s unclear how it could survive down to zero temperature or generate a conductivity saturation. Instead, one might be tempted to picture this new metallic state as a set of superconducting puddles, but this would not solve the central problem of conductivity saturation: In this scenario, either the superconducting puddles are close enough to short-circuit the entire material, giving infinite conductivity, or they are distant enough that conduction from one puddle to the next is not possible, causing the insulating behavior of the material to prevail. Hence, the observed residual conductivity implies that neither paraconductivity nor superconducting puddles are realized, and somehow Cooper pairs (more or less phase coherent) share the space with unpaired electrons (more or less localized) (Fig. 1).
The failed superconductor state is yet to be explored by thermoelectric, thermodynamic, and spectroscopic probes. It is worth noting that this is not the only case of anomalous 2D metallicity. Two decades ago, another metallic state was unexpectedly discovered in 2D heterostructures at the limit of ultralow density [7]. Taken together, these two cases represent a paradigm shift in many-body quantum mechanics by implying that, against the predictions of theories assuming noninteracting electrons, 2D metallicity takes place. Such results remind us again that, despite its impressive accomplishments, quantum theory cannot yet tackle strong interactions among electrons. We can anticipate that other well-established expectations of today’s weakly interacting theory may be rejected by tomorrow’s experimental facts.
This research is published in Reviews of Modern Physics.
References
- A. Kapitulnik, S. A. Kivelson, and B. Spivak, “Colloquium: Anomalous metals: Failed superconductors,” Rev. Mod. Phys. 91, 011002 (2019).
- E. Abrahams, P. W. Anderson, D. C. Licciardello, and T. V. Ramakrishnan, “Scaling theory of localization: Absence of quantum diffusion in two dimensions,” Phys. Rev. Lett. 42, 673 (1979).
- A. Yazdani and A. Kapitulnik, “Superconducting-insulating transition in two-dimensional -MoGe thin films,” Phys. Rev. Lett. 74, 3037 (1995).
- I. Tamir et al., “Extreme sensitivity of the superconducting state in thin films,” arXiv:1804.04648.
- J. Garcia-Barriocanal, A. Kobrinskii, X. Leng, J. Kinney, B. Yang, S. Snyder, and A. M. Goldman, “Electronically driven superconductor-insulator transition in electrostatically doped thin films,” Phys. Rev. B 87, 024509 (2013).
- A. Larkin and A. Varlamov, Theory of Fluctuations in Superconductors, International Series of Monographs on Physics, Vol. 127 (Clarendon Press, Oxford, 2005)[Amazon][WorldCat].
- A. A. Shashkin and S. V. Kravchenko, “Recent developments in the field of the metal-insulator transition in two dimensions,” arXiv:1811. 11828.