Photonic Ising Machines Go Big
In the traveling salesman problem, a time-conscious peddler tries to find the shortest route connecting many cities. To find his solution, he must compare all possible paths—a computation that grows exponentially harder as the number of cities grows. This and other “combinatorial optimization problems” are ubiquitous in business, science, and engineering, and researchers are exploring novel approaches to solve them. But a promising tactic is to map these problems to a statistical model for interacting spins known as the Ising model, which is then solved on a special processor known as an Ising machine. Davide Pierangeli and colleagues at the University of Rome have now realized the largest photonic version of such a machine by representing more than ten thousand spins with a spatially modulated light field [1]. Compared to existing machines, theirs is easier to scale up to accommodate many more spins. With larger machines, researchers could potentially tackle complex optimization problems, such as determining how a protein folds based on its amino acid sequence.
Originally proposed to model ferromagnets, the Ising model describes a network of spins that can point only up or down. Each spin’s energy depends on its interaction with neighboring spins—in a ferromagnet, for instance, each spin will prefer to align with its closest neighbors. Roughly speaking, an Ising machine finds the spin configuration that minimizes the energy of the interacting spins. For a suitable set of spin interactions, this solution can then be translated into the solution of some other optimization problem. Although the algorithms that run an Ising machine typically yield only an approximation of the true ground state, they are often much faster than exact methods.
Optical versions of Ising machines encode a spin state and/or the interaction between spins in the phase and amplitude of a light field. Such machines can be much faster than those based on other encoding schemes (such as atoms or magnets): they are able to process data at light speed and in parallel, through multiple spatial or frequency channels. They can also take advantage of passive components, which perform a mathematical operation many times at fixed energy cost. Finally, the quantum nature of photons provides a natural source of noise, which mimics the temperature fluctuations of a real statistical system.
Inspired by these perks, researchers have developed several photon-based Ising machines using networks of optical parametric oscillators [2–5] and of optical fibers [6, 7]. These photonic machines have been employed to solve optimization problems and to study the phases of spin systems [8, 9]. So far, however, these prototypes haven’t been scalable beyond a few hundred or a few thousand spins because of the effects of decoherence or dispersion, which limit the machines’ practical use.
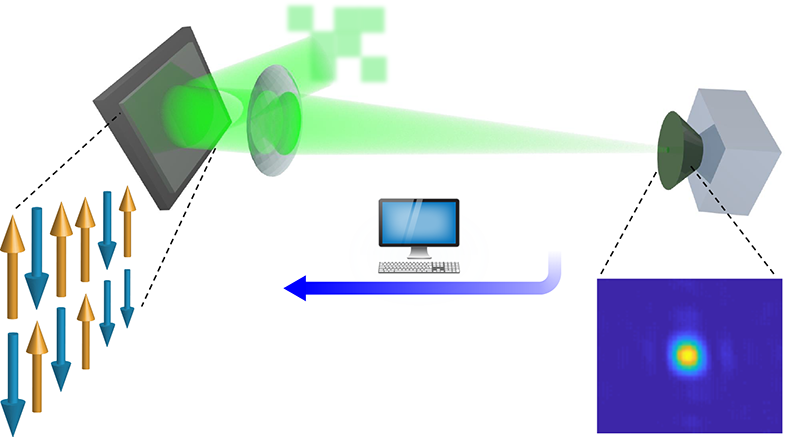
Pierangeli et al. surpass this limit with an optical Ising machine that handles tens of thousands of spins—and possibly more [1]. Their success results from a setup that combines two features: It encodes and processes the spin interactions all at once (spatial multiplexing), and it largely relies on free-space optics, avoiding the need to machine and assemble numerous tiny parts. The researchers used a so-called spatial light modulator (SLM) to imprint a phase of 0 or 𝜋 at distinct points on the wave front of a laser beam. This binary phase mimics the up or down state of a spin. The team set the interactions between the spins by spatially modulating the beam’s intensity. With these parameters in play, an experiment then consisted of repeated cycles of the following steps (Fig. 1). First, send an intensity-modulated laser beam through the SLM to imprint the spins. Then, record the beam in a CCD camera and compare the detected image to a “target image.” Finally, update the SLM settings to minimize the difference between the two images. By design, this step is the same as minimizing the energy of the spin system. After many cycles, a readout of the SLM will reveal the spin configuration corresponding to the ground state for the chosen interactions, a recently proposed process for evolving the spin states that is known as recurrent feedback [10].
In a proof-of-principle demonstration, Pierangeli et al. set the spin interactions for a simple ferromagnet and showed that their machine yielded the ground state expected at low temperature from mean-field-theory calculations. (The “temperature” of their system is fixed by the various noise sources in the experiment.) In a second experiment, the researchers adjusted the spin interactions to simulate a type of magnet known as a spin glass, where the spin couplings are randomly distributed. Thanks to their machine’s ability to handle many spins, the team was able to analyze how physical observables like the phase’s magnetization and correlation lengths scaled with the number of spins.
The work by Pierangeli et al. realizes one of—if not the—largest physical Ising machines ever demonstrated. In principle, it could be scaled up further because larger laser wave fronts can be used to encode more spins, allowing massive numbers of spins to be handled at once. One exciting feature of the researchers’ work is their use of intrinsic photon noise to play the role of temperature [10]. With improved control of the noise level, they will have a temperature “knob” with which to drive and study phase transitions of spin systems. Another interesting direction for their work might be deep learning. This artificial intelligence tool relies on ultrafast and large-scale matrix-to-vector multiplications, an operation that could be performed on a fast optical processor like an Ising machine [2, 10]. For all of these applications, the researchers will need to demonstrate that they can implement operations at close to light speed and for larger numbers of spins. They will also need to reduce the time it takes to update their SLM.
Broader applications will require more radical changes to their machine. For example, creating an effective “bias” magnetic field on the spins is usually required to map the Ising model to the traveling salesman problem. But even with this hurdle ahead, Pierangeli et al. have brought optical Ising machines closer to solving real-world problems by making the devices scalable.
This research is published in Physical Review Letters.
References
- D. Pierangeli, G. Marcucci, and C. Conti, “Large-scale photonic Ising machine by spatial light modulation,” Phys. Rev. Lett. 122, 213902 (2019).
- P. L. McMahon et al., “A fully programmable 100-spin coherent Ising machine with all-to-all connections,” Science 354, 614 (2016).
- T. Inagaki et al., “A coherent Ising machine for 2000-node optimization problems,” Science 354, 603 (2016).
- A. Marandi, Z. Wang, K. Takata, R. L. Byer, and Y. Yamamoto, “Network of time-multiplexed optical parametric oscillators as a coherent Ising machine,” Nat. Photon. 8, 937 (2014).
- T. Inagaki, K. Inaba, R. Hamerly, K. Inoue, Y. Yamamoto, and H. Takesue, “Large-scale Ising spin network based on degenerate optical parametric oscillators,” Nat. Photon. 10, 415 (2016).
- M. R. Vázquez et al., “Optical NP problem solver on laser-written waveguide platform,” Opt. Express 26, 702 (2018).
- K. Wu, J. García de Abajo, C. Soci, P. P. Shum, and N. I. Zheludev, “An optical fiber network oracle for NP-complete problems,” Light Sci. Appl. 3, e147 (2014).
- N. Ghofraniha, I. Viola, F. Di Maria, G. Barbarella, G. Gigli, L. Leuzzi, and C. Conti, “Experimental evidence of replica symmetry breaking in random lasers,” Nat. Commun. 6, 6058 (2015).
- D. Pierangeli, A. Tavani, F. Di Mei, A. J. Agranat, C. Conti, and E. DelRe, “Observation of replica symmetry breaking in disordered nonlinear wave propagation,” Nat. Commun. 8, 1501 (2017).
- C. Roques-Carmes et al., “Photonic recurrent Ising sampler,” arxiv:1811.02705.