Supermassive Black Hole May Constrain Superlight Dark Matter

Eric Armengaud

Viewpoint

Supermassive Black Hole May Constrain Superlight Dark Matter

IRFU, CEA, University of Paris-Saclay, F-91191 Gif-sur-Yvette, France

July 10, 2019• Physics 12, 78

An interpretation of the black hole image taken by the Event Horizon Telescope hints of new constraints on the mass of dark matter.

Figure caption — **Figure 1:** Image of the supermassive black hole M87*, taken by the Event Horizon Telescope.

Recently, astronomers obtained the first image of the accretion disk around the horizon of a supermassive black hole using a world-wide network of radio observatories called the Event Horizon Telescope (EHT) [1]. Black-hole-related observations can provide tests of new, exotic physical processes and, in particular, they can point toward or exclude some dark matter models. Hooman Davoudiasl and Peter Denton from Brookhaven National Laboratory in New York have now interpreted the EHT observations in the context of an appealing ultralight dark matter scenario, referred to as fuzzy dark matter (FDM) [2]. The researchers studied the implications of the EHT black hole’s estimated rotation rate on the so-called superradiance effect—which is an enhanced particle emission process that can slow the rotation rate of a black hole. As current observations suggest that the black hole is rapidly spinning, Davoudiasl and Denton were able to place new bounds on acceptable masses for dark matter.

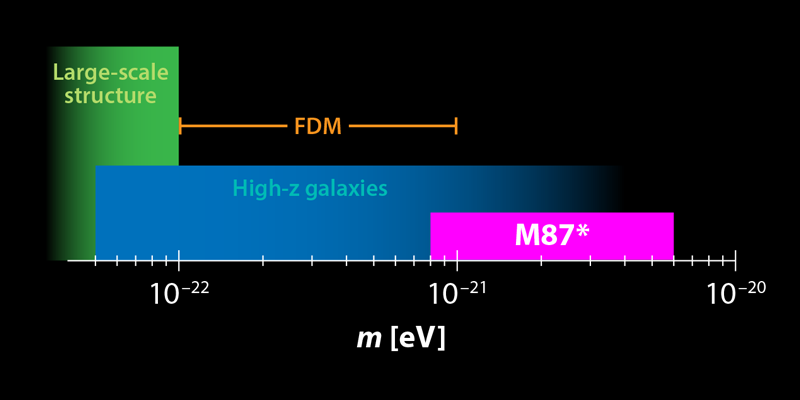
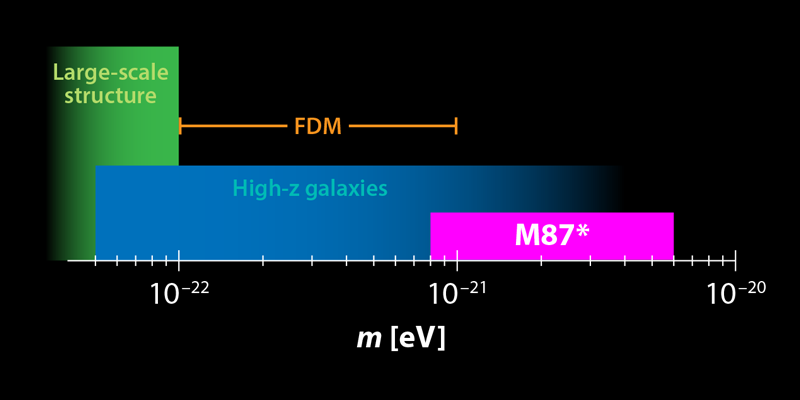
Dark matter, a key ingredient of modern cosmology, is a physical object whose gravitational effects are observed in a wide range of systems, from small, nearby galaxies to the primordial plasma as probed by the cosmic microwave background. However, its fundamental nature is still completely unknown. A popular model is the WIMP or weakly interacting massive particle, which has an expected mass on the order of $100 GeV ∕ c^{2}$ ( $1 0^{11} eV ∕ c^{2}$ ). Several ongoing experiments are searching for WIMPs, but nothing has turned up yet. As a consequence, researchers are turning their attention to a large variety of dark matter models, with masses in the range from around $1 0^{- 22} eV ∕ c^{2}$ to several times a solar mass ( $1 0^{66} eV ∕ c^{2}$ ). It’s at the light end of this spectrum that the recent EHT image (Fig. 1) plays a role.

The FDM scenario assumes that dark matter particles are many orders of magnitude lighter than other particles. Such ultralight particles appear in several scenarios beyond the standard model of particle physics [3, 4]. In particular, the existence of light bosonic fields (specifically, pseudoscalars) is a generic prediction of string theory. The particles associated with these fields have a wide range of masses, but in order for them to constitute a large fraction of dark matter, their mass must be above roughly $1 0^{- 22} eV ∕ c^{2}$ (see 9 August 2000 Focus story). The reason for this lower bound is that dark matter particles lighter than this value would have had a very large quantum uncertainty in their position during the early Universe. This spread in position would lead to a smooth density distribution, which is inconsistent with the large-scale galactic structure that is observed today. On the other hand, if the dark matter particles have a mass around or slightly above $1 0^{- 22} eV ∕ c^{2}$ , the large spatial extension of their quantum wave function could actually solve some problems at subgalactic scales with the standard cosmological model, which assumes a heavy dark matter particle. The potential to resolve such issues is one of the main motivations for investigating FDM [5].

So far, researchers have studied the implications of the FDM models on the structure of the Universe at the million-light-year scale. These studies, which analyzed small galaxies at very high redshifts and density fluctuations of the intergalactic medium, provided lower bounds of around $1 0^{- 21} eV ∕ c^{2}$ for the mass of dark matter. However, these bounds are not yet completely robust because of uncertainties, and they cannot easily be extended to larger values of the dark matter mass.

Here’s where black holes enter the story. Around rapidly rotating black holes, general relativity predicts the existence of a region outside the event horizon, named the ergoregion, in which spacetime is “dragged” around the black hole. Under certain conditions, particles in the ergoregion can escape and carry with them energy—and spin—from the black hole. This is the superradiance process [6]. Consider now the case when the particles in question are bosons, with a mass m such that their Compton wavelength is of the order of the event horizon radius, which means m $\sim h c ∕ G M_{BH}$ where $h$ is the Planck constant, $c$ is the speed of light, $G$ is the gravitational constant, and $M_{BH}$ is the mass of the black hole. These boson particles will form an “atom” around the black hole (analogous to usual atoms, with gravity replacing electromagnetism and the black hole replacing the nucleus). The wave function of this atom will overlap with the ergoregion, causing an enhanced emission of particles that rapidly extracts angular momentum from the black hole (see 24 July 2017 Viewpoint).

It is a difficult task to compute the details of this superradiance process in realistic situations [7]. Nevertheless, a generic consequence of the superradiance mechanism is that observing a fast-spinning black hole with a given mass $M_{BH}$ implies that it has not been spun down by the superradiance process and—by extension—there cannot be any light bosons with mass $m$ close to $h c ∕ G M_{BH}$ . There are estimations of the mass and spin for both stellar-mass black holes in our Galaxy and supermassive black holes at the center of other galaxies, which have led to constraints on light bosonic particles with masses around $1 0^{- 11} eV ∕ c^{2}$ and $1 0^{- 17} eV ∕ c^{2}$ , respectively [8]. Note that this mechanism is independent of whether the bosonic particles constitute dark matter or not.

To probe the unexplored dark matter mass range of around $1 0^{- 21}$ to $1 0^{- 18} eV ∕ c^{2}$ with superradiance, particularly massive black holes are needed. The supermassive black hole M87* in the center of the nearby galaxy M87 is the perfect target. The recent EHT observations confirmed that it has a large mass of $6.5 \times 1 0^{9}$ solar masses, while also indicating a high spin rate—based on measurements of a jet associated with M87* [9]. In their new analysis, Davoudiasl and Denton use the EHT results—as well as simple estimations for the superradiance rate and lifetime of M87*—and conclude that light bosons with masses between about $8.5 \times 1 0^{- 22}$ and $4.6 \times 1 0^{- 21} eV ∕ c^{2}$ are unlikely to exist (Fig. 2). This disfavored mass range, which depends on the assumed spins of both the boson and the black hole, places new constraints on dark matter models in the very upper part of the mass range for the FDM scenario.

However, the bounds provided by Davoudiasl and Denton should be taken with a grain of salt and considered as a first step. One reason for caution is that the researchers rely on simple estimates for the superradiance phenomena, which, for example, do not take into account the effects of potential self-interactions between bosonic particles. Also, the EHT observation provided a remarkable confirmation of the mass of M87*, but it could not yet yield a clear estimation of its spin, the crucial parameter in the superradiance process. Analysis of EHT data—by teams inside and outside the collaboration—suggest that the M87* spin is nonzero and could even be close to maximal [10], but further confirmation is needed.

In spite of these cautious words, the results by Davoudiasl and Denton are a significant step in the search for ultralight bosons, whether they constitute dark matter or not. They provide an additional constraint on FDM models, and increase the range of bosonic masses now probed by the superradiance effect.

This research is published in Physical Review Letters.

References

K. Akiyama et al. (The EHT Collaboration), “First M87 Event Horizon Telescope results. I. The shadow of the supermassive black hole,” Astrophys. J. Lett. 875, L1 (2019).
H. Davoudiasl and P. B. Denton, “Ultralight boson dark matter and Event Horizon Telescope observations of M87*,” Phys. Rev. Lett. 123, 021102 (2019).
A. Arvanitaki, S. Dimopoulos, S. Dubovsky, N. Kaloper, and J. March-Russell, “String axiverse,” Phys. Rev. D 81, 123530 (2010).
D. J. E. Marsh, “Axion cosmology,” Phys. Rep. 643, 1 (2016).
W. Hu, R. Barkana, and A. Gruzinov, “Fuzzy cold dark matter: The wave properties of ultralight particles,” Phys. Rev. Lett. 85, 1158 (2000).
R. Penrose, “Gravitational collapse: The role of general relativity,” Riv. Nuovo Cimento 1, 252 (1969).
R. Brito, V. Cardoso, and P. Pani, “Black holes as particle detectors: Evolution of superradiant instabilities,” Class. Quantum Grav. 32, 134001 (2015); W. E. East and F. Pretorius, “Superradiant instability and backreaction of massive vector fields around Kerr black holes,” Phys. Rev. Lett. 119, 041101 (2017).
A. Arvanitaki, M. Baryakhtar, and X. Huang, “Discovering the QCD axion with black holes and gravitational waves,” Phys. Rev. D 91, 084011 (2015).
K. Akiyama et al. (The EHT Collaboration), “First M87 event horizon telescope results. V. Physical origin of the asymmetric ring,” Astrophys. J. Lett. 875, L5 (2019).
F. Tamburini, B. Thidé, and M. Della Valle, “Measurement of the spin of the M87 black hole from its observed twisted light,” arxiv:1904.07923.

About the Author

Eric Armengaud is a researcher working at the IRFU institute of CEA-Saclay, France. He completed his Ph.D. at the APC and IAP laboratories in Paris, studying extragalactic cosmic rays within the Pierre Auger Observatory. At CEA he dedicated his work to the EDELWEISS underground experiment in the search for WIMP dark matter and lighter axion-like particles. His research now focuses on the use of cosmological observations, especially from wide-field spectroscopic surveys (eBOSS and DESI), to study the properties of dark matter.