Ion Clock Busts into New Precision Regime
Which periodic oscillator would make the best clock? Nobody really knows. But in 1982 Hans Dehmelt—who would later win the Nobel prize for his development of the ion trap—realized that the “ultimate” time keeper might be a single ion, trapped by electric fields and cooled with lasers [1]. The frequency of light emitted by the ion as it transitions between two internal states could, Dehmelt estimated, be measured with a fractional uncertainty of 10−18, allowing a similarly precise definition of the second as a fixed number of cycles of the light wave. Nearly four decades later, researchers have fulfilled Dehmelt’s visionary prediction. Samuel Brewer and colleagues from the National Institute of Standards and Technology (NIST) in Colorado report an Al+ ion clock with a fractional uncertainty of 0.94×10−18, the most precise clock in existence today [2]. Using different ions or neutral atoms in so-called optical lattices, other groups are expected to soon reach the 10−18 milestone [3–7], which would allow for increasingly precise tests of variations in fundamental constants.
Ions, like other atomic systems, have the great advantage that their natural transition frequencies are determined solely by physical constants and quantum mechanics. Provided that the ions are in a controlled environment, this frequency can be reproduced anywhere on Earth or even in space. Dehmelt’s bold prediction stemmed from his realization that an ion’s environment could, in principle, be controlled to near perfection. The combination of laser cooling and ion trapping would allow the ion to be held in a near motionless state, avoiding even the tiniest relativistic shifts to the ion frequency.
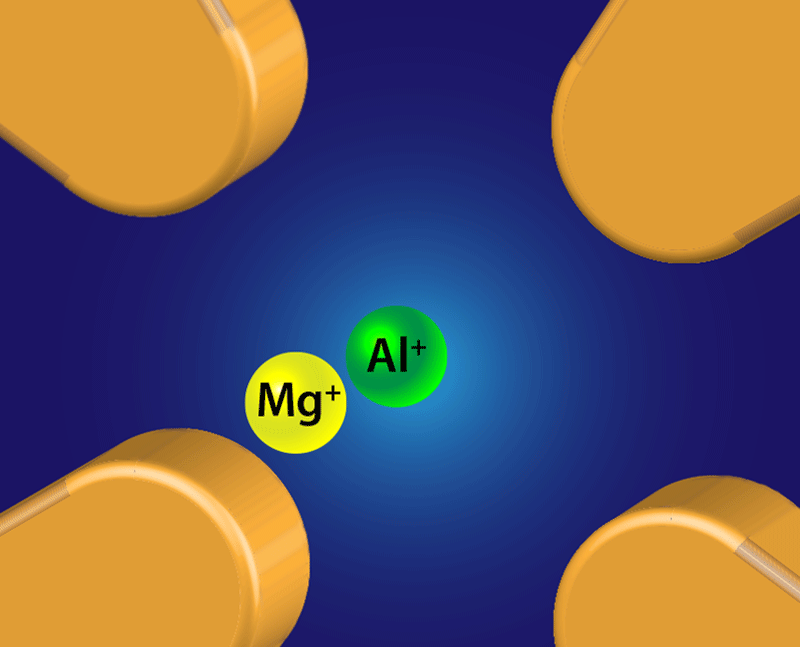
In his 1982 paper, Dehmelt identified 27Al+ specifically as an excellent candidate for a high-precision clock [1]. This ion has a transition of around 1.21×1015Hz with an extremely small natural linewidth of 8mHz [8]. And compared with other optical clock systems, the Al+ transition is much less sensitive to blackbody radiation or to external magnetic- and electric-field gradients [6]. But the ion has two serious drawbacks. Its most accessible atomic transition for laser cooling is in the vacuum ultraviolet and therefore impractical for today’s laser technology. For similar reasons, the quantum state of the ion is difficult to detect using a conventional light-scattering measurement. In 2005, the NIST group showed they could circumvent these problems by trapping the Al+ next to another ion (Fig. 1) that can be more easily laser cooled and detected [9]. As the partner ion is cooled, it pulls heat from the Al+ ion through the Coulomb interaction. The same interaction can be harnessed to “imprint” the Al+ electronic state on the motional states of its partner, which can be measured to characterize the Al+ ion. Applying this partnering technique, known as quantum logic spectroscopy, the NIST researchers were able, in 2007, to measure the Al+ clock transition with 5×10−15 uncertainty [8].
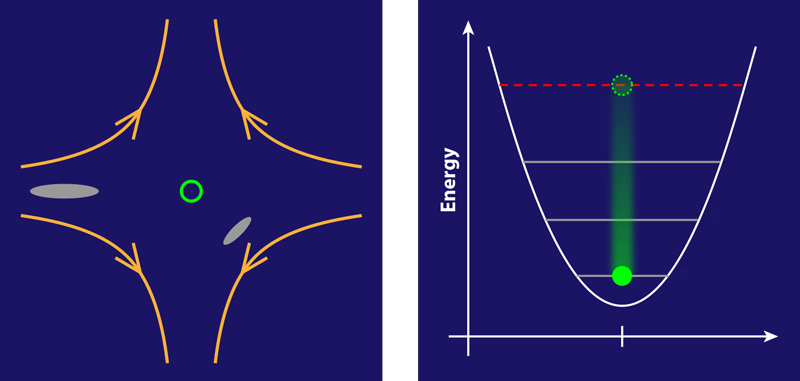
With the cooling technique in place, the NIST group has spent the last decade contending with the main perturbation to the Al+ clock frequency: residual motion of the ion in the trap. This motion comes primarily from two sources—the trap and thermal effects (Fig. 2)—both of which affect Al+ more than they do other clock ions because of its small mass. The first source, known as micromotion, arises from the trap itself, which is made of multiple electrodes whose voltages oscillate at radio frequencies (rf) and produce a “quadrupole” electric-field configuration (Fig. 2, left). Ideally, the ion sits where this rf field is zero. But imperfections in the trap can displace the ion into a region of finite rf field, which perturbs the ion’s energy levels (through the ac Stark effect). The field also accelerates the ion, resulting in time dilation of the clock frequency. In their new work, Brewer et al. reduced the uncertainty resulting from these two effects by operating the trap at a lower rf and voltage and by making real-time corrections to the remaining micromotion.
The second source, called secular motion (Fig. 2, right), comes from the thermal motion of the trapped ion and its partner ( 25Mg+in the new experiments.) The ion pair has 6 motional degrees of freedom, each of which contributes to a time-dilation shift. Electric field noise and other sources heat the ions, but a new trap design helped the researchers to minimize the heating rate while they were measuring the ion frequency. Building on earlier work [10], they also used a laser-cooling scheme that brought the ion pair to near its 3D motional ground state.
Addressing the motional perturbations was a big part of crossing the long-sought 10−18 uncertainty threshold. But another crucial step was reducing the uncertainty that exists because an external magnetic field is needed to define the quantization axis of the quantum logic clock. This field shifts the clock transition by an amount that varies as the square of the field strength multiplied by a “sensitivity” coefficient, imposing a fractional shift of approximately 10−15. Brewer and colleagues halved the uncertainty from this “quadratic Zeeman shift” by accurately measuring the field strength (in situ, via the Al+ ion) and by developing an improved method of measuring the sensitivity coefficient [11]. With the lowering of the uncertainties from micromotion ( 5.9×10−19), secular motion ( 2.9×10−19), the quadratic Zeeman shift ( 3.7×10−19), and other sources, the team reports a combined uncertainty of 9.4×10−19.
Researchers have made impressive progress with optical clocks in the last 20 years, reducing the uncertainties by 4 orders of magnitude. This success came from countless improvements in experimental methods, including breakthroughs in laser stabilization, laser manipulation of atomic states, laser cooling, and, in particular, frequency measurement. On its own, an ion emitting at a precise frequency isn’t enough to make a clock—the oscillations of light have to be counted, a step that was enabled by the development of femtosecond frequency combs.
Already, today’s best optical clocks are sufficiently precise to benefit their intended applications—such as redefining the SI second, mapping Earth’s gravitational potential, testing fundamental physics, and navigation. Still, it’s only natural that 10−19 will become the new goal, both for the intrinsic challenge and to continue the long tradition of precision measurements that have led to discoveries about the Universe.
This research is published in Physical Review Letters and Physical Review A.
References
- H. G. Dehmelt, “Mono-ion oscillator as potential ultimate laser frequency standard,” IEEE Trans. Instrum. Meas. IM-31, 83 (1982).
- S. M. Brewer, J.-S. Chen, A. M. Hankin, E. R. Clements, C. W. Chou, D. J. Wineland, D. B. Hume, and D. R. Leibrandt, “27Al+ quantum-logic clock with a systematic uncertainty below 10−18,” Phys. Rev. Lett. 123, 033201 (2019).
- N. Huntemann, C. Sanner, B. Lipphardt, C. Tamm, and E. Peik, “Single-ion atomic clock with 3×1018 systematic uncertainty,” Phys. Rev. Lett. 116, 063001 (2016).
- W. F. McGrew et al., “Atomic clock performance enabling geodesy below the centimetre level,” Nature 564, 87 (2018).
- T. Bothwell, D. Kedar, E. Oelker, J. M. Robinson, S. L. Bromley, W. L. Tew, J. Ye, and C. J. Kennedy, “JILA SrI optical lattice clock with uncertainty of 2.0×10−18,” arXiv:1906.06004.
- A. D. Ludlow, M. M. Boyd, J. Ye, E. Peik, and P. O. Schmidt, “Optical atomic clocks,” Rev. Mod. Phys. 87, 637 (2015).
- M. Abdel-Hafiz et al., “Guidelines for developing optical clocks with 10−18 fractional frequency uncertainty,” arXiv:1906.11495.
- T. Rosenband et al., “Observation of the 1S0→3P0 clock transition in 27Al+,” Phys. Rev. Lett. 98, 220801 (2007).
- P. O. Schmidt, T. Rosenband, C. Langer, W. M. Itano, J. C. Bergquist, and D. J. Wineland, “Spectroscopy using quantum logic,” Science 309, 749 (2005).
- J.-S. Chen, S. M. Brewer, C. W. Chou, D. J. Wineland, D. R. Leibrandt, and D. B. Hume, “Sympathetic ground state cooling and time-dilation shifts in an 27Al+ optical clock,” Phys. Rev. Lett. 118, 053002 (2017).
- S. M. Brewer et al., “Measurements of 27Al+ and 25Mg+ magnetic constants for improved ion-clock accuracy,” Phys. Rev. A 100, 013409 (2019).