A Crowd Freezes Up
Moving in a crowd is part of our daily lives, be it walking in subway corridors, driving on motorways, or queuing for museums. The experience can suddenly become unpleasant when the crowd gets too dense, causing collisions and jams. But what exactly determines the transition between a smooth one-way flow and a nightmarish jam? Can one predict and avoid this transition? Is jamming gradual or catastrophic? To answer questions like these, Denis Bartolo of the Ecole Normale Supérieure de Lyon, France, and colleagues studied an artificial crowd made of microscopic motorized beads [1]. They showed that, beyond a certain bead density, a large part of the crowd comes to a halt, “freezing” much like water turning into ice. The researchers show that the freezing results from a long-sought phase transition unique to ensembles of self-propelled particles.
Researchers have identified many types of collective behavior in groups of mobile individuals. An intriguing example is the emergence of directed motion in the absence of a leader, or “flocking,” as displayed by birds and fish schools. To understand the behavior of groups, researchers describe them as “active matter”—ensembles of interacting, self-propelled particles. Using a computer model, physicist Tamás Vicsek and colleagues showed in 1995 that when neighboring particles tend to align their velocities, a common direction of motion arises spontaneously above a certain crowd density [2]. Vicsek’s model is now the paradigm for elucidating flocking in many systems.
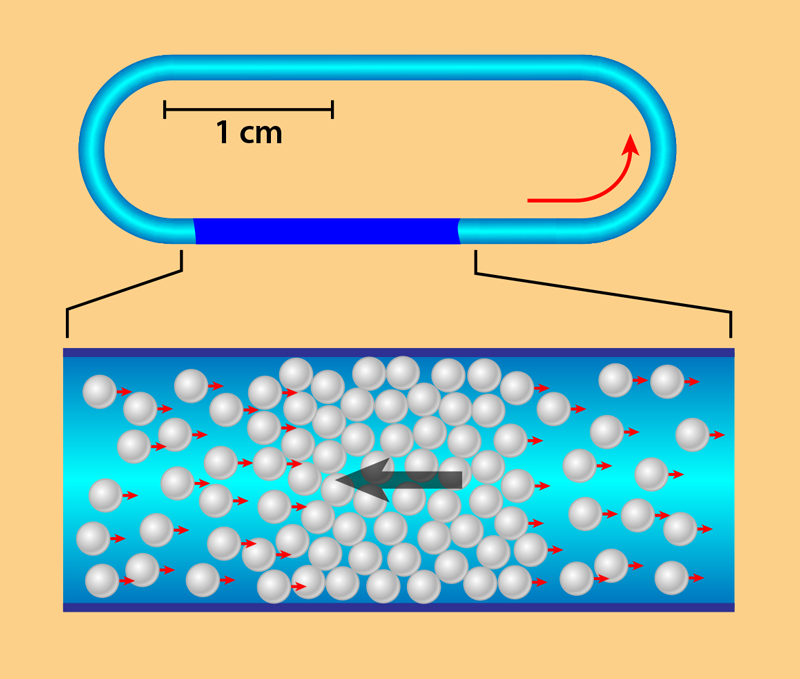
In 2013, Bartolo’s group provided a valuable platform to study flocking in a controlled experimental setting [3]. Their setup consists of millions of polystyrene microbeads suspended in a liquid kept between two glass plates. The beads roll onto the bottom plate, exploring a centimeter-sized racetrack-shaped enclosure (Fig. 1, top). Their rotation is powered by the Quincke effect, which arises when an electric field is applied to an insulating sphere immersed in a conducting fluid. Using this setup, the team previously observed that an increase in particle density could trigger a Vicsek-like transition from a “gas” of randomly moving particles to a flock of millions of particles cruising along the track in the same direction [3].
Until now, however, experiments had not tackled high-density ensembles of particles, despite their relevance to many practical situations. Such studies require a large number of well-controlled, self-propelling particles, all of which receive a sufficient and uniform energy input. The experiments must also prevent particle aggregation. The setup from Bartolo’s team fulfills these challenging demands by simply placing large amounts of the microbeads—which are commercially available—in the racetrack under an applied electric field. The field serves as a “fuel” that inputs energy over the entire racetrack. What’s more, the field induces dipolar repulsion between the particles, preventing their aggregation.
Compared with previous studies, the researchers were able to access much higher densities—defined as the percent coverage of the racetrack’s surface. The experiments show that a smoothly flowing flock forms above a density of a few percent and survives up to fairly high crowding—until about half the surface is covered. Above a critical density of 55%, solid jams start to nucleate within the flock and merge into a single, stable jam. The onset of jamming is sudden, with a surprisingly large first stable jam that involves millions of particles covering a tenth of the racetrack. While particles inside the jam are arrested, the jam propagates against the flow of the surrounding flock as a compact wave, accumulating particles at its advancing front, while losing particles to the flock from its retreating end (Fig. 1, bottom). As crowding further increases, the jam becomes larger, until it spans the whole particle assembly at 70% coverage.
The authors find that the formation of the jam has the hallmarks of a first-order phase transition, much like the freezing of water. One such hallmark is nucleation, in which jams smaller than a critical size disappear, while larger ones grow and merge until a stable jam coexists with the flocking phase. In the same way that water freezes via the nucleation of crystals in the liquid, one could say that the fluid flock freezes via the nucleation of solid jams. Two other features support a first-order transition. First, when the jam and the fluid state coexist, they have constant densities. Second, hysteretic effects occur at the onset of solidification.
What causes this extended freezing of the flock? The authors rule out crystallization, which, according to prior work [4], could only occur at about 70% coverage, well beyond the onset of jamming; and aggregation, which isn’t possible since the particle interactions are repulsive. Having eliminated two likely culprits, they focus on a phenomenon known as motility-induced phase separation (MIPS). MIPS is predicted to occur in active matter when crowding slows down the particles’ motion [5, 6]. This slowdown can be due to various factors, including particle collisions. When sufficiently frequent, the collisions can cause the particles to cluster in high-density, solid-like islands, coexisting with a fluid-like phase, even in the absence of attraction [5, 6].
To picture how MIPS occurs, imagine a busy arena of bumper cars in an amusement park. Suppose that the density of cars increases in one spot, making cars likely to collide there. Enthusiastic drivers keep accelerating while colliding (like self-propelled particles), thereby locking their cars into a cluster as if they were mutually attracted. Cars therefore slow down and accumulate in dense regions, and when the effect is sufficiently strong, a positive feedback mechanism can amplify this instability. This growth leads to a phase separation between clusters of cars (the solid) and areas where cars keep moving more freely (the fluid).
A similar picture holds in the team’s experiment but with a twist. Instead of collisions, what slows down the particles are hydrodynamic effects that hinder the particles’ rotation when they get close to each other. The authors’ calculations show that this density-dependent slowdown is sufficient for MIPS to occur and that MIPS can fully explain the observed features of jamming. So far, MIPS had been predicted by theory and simulations, but experimental evidence was restricted to the observation of dynamic clusters of limited size [7]. By showing large-scale phase separation, the new experiments provide conclusive evidence for MIPS.
MIPS may turn out to be a general feature of self-propelled systems, independent of the specific mechanism that causes individuals to slow down in crowded areas, such as physical interactions, sensing of the surroundings, or mutual communication [8]. While hydrodynamics can describe how crowds of people flow [9], MIPS may help researchers understand why they jam, which would be relevant for crowd-control strategies in public gatherings like music festivals and public demonstrations. The design of autonomous systems, such as smart-car fleets or robots swarms, may also need to account for motility-induced transitions, so as to avoid jamming-prone conditions.
This research is published in Physical Review X.
References
- D. Geyer, D. Martin, J. Tailleur, and D. Bartolo, “Freezing a flock: Motility-induced phase separation in polar active liquids,” Phys. Rev. X 9, 031043 (2019).
- T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen, and O. Shochet, “Novel type of phase transition in a system of self-driven particles,” Phys. Rev. Lett. 75, 1226 (1995).
- A. Bricard, J. B. Caussin, N. Desreumaux, O. Dauchot, and D. Bartolo, “Emergence of macroscopic directed motion in populations of motile colloids,” Nature 503, 95 (2013).
- G. Briand and O. Dauchot, “Crystallization of self-propelled hard discs,” Phys. Rev. Lett. 117, 098004 (2016).
- J. Stenhammar, A. Tiribocchi, R. J. Allen, D. Marenduzzo, and M. E. Cates, “Continuum theory of phase separation kinetics for active brownian particles,” Phys. Rev. Lett. 111, 145702 (2013).
- M. E. Cates and J. Tailleur, “Motility-induced phase separation,” Annu. Rev. Condens. Matter Phys. 6, 219 (2015).
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger, and T. Speck, “Dynamical clustering and phase separation in suspensions of self-propelled colloidal particles,” Phys. Rev. Lett. 110, 238301 (2013); J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine, and P. M. Chaikin, “Living crystals of light-activated colloidal surfers,” Science 339, 936 (2013); F. Ginot, I. Theurkauff, F. Detcheverry, C. Ybert, and C. Cottin-Bizonne, “Aggregation-fragmentation and individual dynamics of active clusters,” Nat. Commun. 9, 696 (2018).
- B. Liebchen and H. Löwen, “Synthetic chemotaxis and collective behavior in active matter,” Acc. Chem. Res. 51, 2982 (2018).
- N. Bain and D. Bartolo, “Dynamic response and hydrodynamics of polarized crowds,” Science 363, 46 (2019).