Naturalness Hits a Snag with Higgs
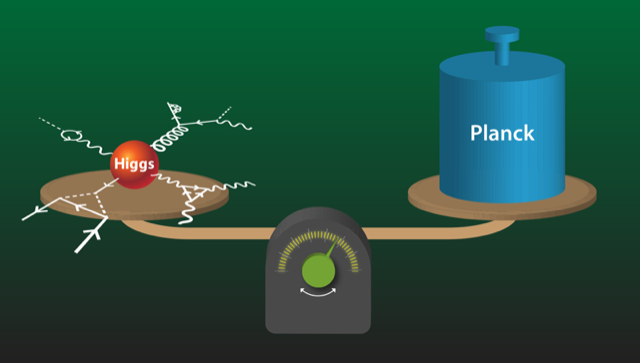
The discovery of the Higgs boson at the Large Hadron Collider (LHC) in 2012 illuminated the mechanism of electroweak symmetry breaking, through which the electromagnetic and weak nuclear forces emerge from a unified electroweak force. But if the Higgs discovery answered the question of how electroweak symmetry breaking occurs, it left open the further question of why this breaking occurs at around 250 GeV—an energy that is far removed from other energy scales in particle physics. This energy mismatch goes by the name of the electroweak hierarchy problem, and it is one of the great mysteries in physics. The central question is often reframed in terms of the Higgs mass: why does the Higgs weigh 125GeV∕c2 when a naïve prediction (Fig. 1) would place it 17 orders of magnitude higher, near the Planck mass?
Particle physicists have previously faced incongruities like this, in which parameters that seem closely related have values that are far from each other. One way of dealing with these large gaps, or hierarchies, is to use the “naturalness” strategy. Naturalness is a theoretical perspective, which assumes that nature actually does choose values that are close to each other, but this only becomes evident when one identifies a symmetry or other mechanism that explains the apparent discrepancy. This strategy has successfully explained the values of the electron mass and the pion mass, as well as predicted the existence of the charm quark. One would assume the same strategy could explain the Higgs mass. But so far it hasn’t. Physicists are therefore proposing alternative strategies that go beyond the usual naturalness paradigm.
The Higgs Paradigm
One of the first physicists to address hierarchy problems was Paul Dirac, who was struck by the enormous difference between the proton mass ( ∼1GeV∕c2) and the Planck mass ( ∼1019GeV∕c2). Dirac’s desire to understand this hierarchy motivated him to create an elaborate cosmology in which fundamental constants varied as a function of time [1]. Although Dirac’s proposed answer turned out to be wrong, his interest in the question was justified. Decades after his work on the subject, the explanation for the proton mass emerged from considerations of the strong force, specifically its increase in strength at long range—opposite to what occurs for other forces. This behavior, which is called asymptotic freedom, sets the mass scale for the proton and other quark bound states.
It is tempting to posit the same asymptotic-freedom mechanism to explain the energy scale of electroweak symmetry breaking—a proposal known as technicolor [2]. However, the discovery of the Higgs boson (Fig. 2) suggests that a qualitatively different mechanism is at play. The Higgs boson is the particle excitation of a scalar field, whose value in the vacuum is what breaks the unified electroweak force into its low-energy remnants and gives masses to the fundamental particles of the standard model (see Viewpoint: A Fuller Picture of the Higgs Boson). But if electroweak symmetry is indeed broken by the Higgs field’s behavior, the mystery only deepens. The problem can be stated like this: the Higgs gives mass to all other particles, but all other particles give mass to the Higgs—through quantum corrections to the mass term of the scalar field. This pile-on effect should drive the Higgs mass to the Planck scale, but the Higgs has resisted this expected weight gain in view of the electroweak hierarchy problem.
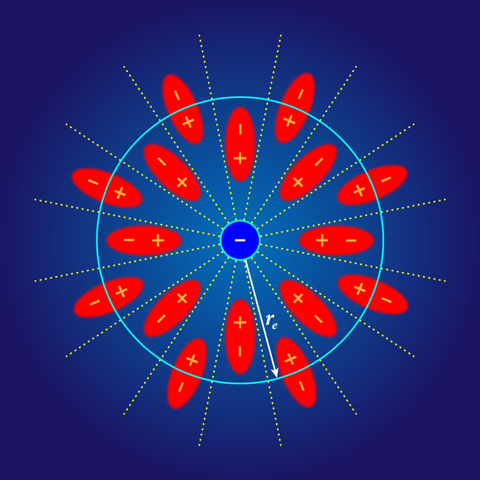
The essence of the hierarchy problem is familiar to anyone who has taken undergraduate electrodynamics. The electron is surrounded by an electric field that diverges at small distances from the electron’s point-like charge. The energy in this field is called the self-energy, and it should contribute to the electron’s mass (just as quantum corrections contribute to the Higgs mass). But if one uses the current bounds on the radius of the electron, re<10−18cm, then the self-energy contribution to the mass is greater than 100GeV∕c2—which is a million times the measured rest mass of 511keV∕c2 for the electron. One could assume that the electron’s “bare” mass—the mass not coming from the electric field—somehow cancels most of the self-energy contribution, but that kind of balancing act would require these mass values to be bewilderingly close to each other—to a precision of one part in a million.
Such fine tuning seems unnatural—as if the electron were put together like a delicate watch. But this picture can be avoided by making the self-energy naturally smaller through a change in the electric field. This change comes out of the relativistic quantum theory of electrodynamics, which predicts that the strong electric field around the electron’s charge causes the spontaneous formation and rapid annihilation of virtual electron-positron pairs. These so-called quantum loops screen the electron charge, thus modifying the field at radii near to re (Fig. 3). As a result, the self-energy tunes itself down to precisely the same order as the observed rest energy, rendering the outcome “natural.”
If one digs deeper, one finds that this electron-mass explanation relies on a symmetry of nature. Specifically, the electron and positron obey chiral symmetry at energies greater than the electron mass. At lower energies, chiral symmetry is broken, which fixes the self-energy quantum corrections to a value near the electron mass. Symmetry-based explanations are prime examples of the naturalness approach. But there are other ways by which naturalness can solve a hierarchy or fine-tuning problem. For example, the mass of the charged pion can appear fine tuned, but the problem disappears once you treat the pion as a composite particle made of two quarks. In general, the naturalness strategy tells physicists to be on the lookout for the appearance of new physics (new symmetries, new particles) whenever nature seems to be fine tuning its parameters.
Higgs Hitch
So, where should new physics appear to solve the electroweak hierarchy problem? Calculations of the Higgs mass suggest the picture should change at energies around 500 GeV, well within the range of the energies being probed at the LHC.
As for what might show up at this scale, the analogy with other states in the standard model suggests two obvious options: compositeness and supersymmetry. In the first case, the Higgs is considered to be like the pion, a bound state of lighter particles. Such a composite Higgs would be held together by new strong interactions, which would entail the appearance of additional particles. Alternatively, the Higgs could be like the electron. This explanation is a bit trickier, since the chiral symmetry explaining the electron mass is unique to fermions. But a new symmetry relating the Higgs boson to a new fermion would allow a screening mechanism to develop around the Higgs and this fermion, which would explain the lightness of both particles. Such a symmetry relating bosons and fermions is known as supersymmetry [3, 4].
These two options closely follow the logic of previous naturalness solutions. As such, they have been the dominant paradigms for solving the electroweak hierarchy problem over the past 40 years. But both frameworks predict an abundance of new particles that have—thus far, at least—not turned up at the LHC. While it is entirely possible that the new particles predicted by compositeness or supersymmetry lie just around the corner, the null results may be telling us that these ideas are akin to Dirac’s explanation for the proton mass: they are motivated, but do not reflect the path that nature has chosen. But if not supersymmetry or compositeness, what else could render the Higgs mass natural?
Other-Naturalness
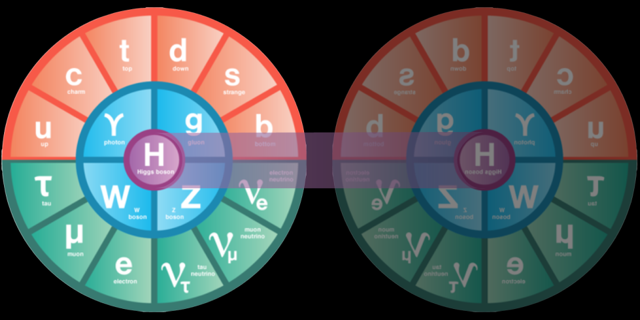
One possibility is that symmetries are still at play but in an unexpected form. In this case, the unexpected symmetry relates the standard model to an identical twin, which has its own particles and interactions that are mirror reflections of those in the standard model [5]. In these “twin Higgs” scenarios, the only connection between the standard model and its mirror twin are the Higgs bosons of the two sectors (Fig. 4). The particles of the standard model and their mirror counterparts act in tandem to control the self-energy of the Higgs, explaining at least some (but not all) of the hierarchy between the weak scale and the Planck scale.
Twin Higgs models could offer unique experimental signatures. Although these models predict a host of new particles—an entire standard-model’s-worth near the weak scale—the mirror particles do not interact via standard model forces, so they could have evaded detection at the LHC. Even so, they may not be entirely invisible. The strong interactions of the mirror sector lead to bound states, just like in the standard model, giving rise to a zoo of mirror mesons and baryons. Some of these particles can mix with the Higgs, providing a portal through which mirror particles can be produced and eventually decay back into standard model particles. Remarkably, these processes are slow enough that mirror particles, if produced at the LHC, would travel distances ranging from centimeters to kilometers before decaying. Detecting such long-lived particles requires a dedicated approach to recording and analyzing data at the LHC, which the CMS and ATLAS collaborations are energetically pursuing.
Another possibility is that symmetries play no decisive role, but rather, the Higgs mass is determined dynamically by the evolution of other fields in the early Universe—similar in spirit to Dirac’s proposed solution for the proton mass. Specifically, this idea assumes a new field, called the relaxion field [6], that behaves like the hypothetical axion field, which theorists have proposed as a fix to a fine-tuning problem in nuclear physics. The amplitude of the relaxion field, which evolves along a gently sloping potential in the early Universe, helps to control the mass of the Higgs. In other words, the Higgs mass is determined by the combination of self-energy from known standard model fields and the background value of the relaxion—both of which may be very large in the early Universe. Only when the total mass of the Higgs becomes small, do features appear in the relaxion potential that cause the evolution to stop, thus fixing the Higgs mass at its observed value.
In this dynamic scenario, the relaxion is the only new particle associated with the value of the weak scale, leaving few possibilities of detectable signals at the LHC but allowing for a wealth of possible signatures in other experiments. Depending on the mass of the relaxion, such signatures might show up as new long-range forces, energy density in dark radiation, rare meson decays at beam dump experiments, or exotic Higgs decays at the LHC [7]. Current axion searches could be sensitive to relaxions, which means any limits placed on axions, such as recent results from the CASPEr experiment [8], would also apply to relaxions.
Finally, it may be that the difficulty of finding a naturalness solution to the hierarchy problem is symptomatic of something larger: the omission of gravity in the standard model. Perhaps the Higgs mass fine-tuning problem will disappear in a theory that unifies quantum mechanics and gravity. We don’t yet have such a theory, but researchers are able to identify quantum field theories that don’t fit with quantum gravity expectations. These gravity-inconsistent theories are said to belong to the “swampland” (see Trend: Cosmic Predictions from the String Swampland). By studying limits of the swampland, researchers can use gravity as a guide for finding a viable theory that goes beyond the standard model. If the Higgs mass happens to be fixed by these sorts of gravity constraints, then one would expect new long-range forces and light particles that couple to the Higgs. These phenomena might be observable in a future Higgs factory (see Opinion: Exploring Futures for Particle Physics).
It’s too soon to say which path nature has chosen among the present options: conventional naturalness hiding just around the corner, other-naturalness in one form or another, or something entirely different. In the meantime, the recent proliferation of ideas surrounding the hierarchy problem has broadened the landscape of possibilities, drawing attention to a host of new experimental signatures to explore.
References
- P. A. M. Dirac, “A new basis for cosmology,” Proc. R. Soc. London A 165, 199 (1938).
- S. Weinberg, “Implications of dynamical symmetry breaking,” Phys. Rev. D 13, 974 (1976).
- P. Fayet, “Spontaneously broken supersymmetric theories of weak, electromagnetic and strong interactions,” Phys. Lett. B 69, 489 (1977).
- S. Dimopoulos and H. Georgi, “Softly broken supersymmetry and SU(5),” Nucl. Phys. B 193, 150 (1981).
- Z. Chacko et al., “Natural electroweak breaking from a mirror symmetry,” Phys. Rev Lett. 96, 231802 (2006).
- P. W. Graham et al., “Cosmological Relaxation of the Electroweak Scale,” Phys. Rev. Lett. 115, 221801 (2015).
- T. Flacke et al., “Phenomenology of relaxion-Higgs mixing,” J. High Energy Phys. 2017, 50 (2017).
- T. Wu et al., “Search for axionlike dark matter with a liquid-state nuclear spin comagnetometer,” Phys. Rev. Lett. 122, 191302 (2019).