Imperfections Lower the Simulation Cost of Quantum Computers

Jordi Tura

Viewpoint

Imperfections Lower the Simulation Cost of Quantum Computers

Lorentz Institute, Leiden University, Leiden, Netherlands
Max Planck Institute of Quantum Optics, Garching, Germany

November 23, 2020• Physics 13, 183

Classical computers can efficiently simulate the behavior of quantum computers if the quantum computer is imperfect enough.

Figure caption — **Figure 1:** Researchers show that they can simulate the above 1D quantum circuit with a classical one if the quantum computer is imperfect enough. $N$ is the number of qubits, and $D$ is the number of gates the circuit executes and is equivalent to increasing time in the image. The colored squares represent random one-qubit gates, and the dots connected to a cross-containing box represent two-qubit Controlled-NOT or Controlled-Z gates.

With a few quantum bits, an ideal quantum computer can process vast amounts of information in a coordinated way, making it significantly more powerful than a classical counterpart. This predicted power increase will be great for users but is bad for physicists trying to simulate on a classical computer how an ideal quantum computer will behave. Now, a trio of researchers has shown that they can substantially reduce the resources needed to do these simulations if the quantum computer is “imperfect” [1]. The arXiv version of the trio’s paper is one of the most “Scited” papers of 2020 and the result generated quite a stir when it first appeared back in February—I overheard it being enthusiastically discussed at the Quantum Optics Conference in Obergurgl, Austria, at the end of that month, back when we could still attend conferences in person.

In 2019, Google claimed to have achieved the quantum computing milestone known as “quantum advantage,” publishing results showing that their quantum computer Sycamore had performed a calculation that was essentially impossible for a classical one [2]. More specifically, Google claimed that they had completed a three-minute quantum computation—which involved generating random numbers with Sycamore’s 53 qubits—that would take thousands of years on a state-of-the-art classical supercomputer, such as IBM’s Summit. IBM quickly countered the claim, arguing that more efficient memory storage would reduce the task time on a classical computer to a couple of days [3]. The claims and counterclaims sparked an industry clash and an intense debate among supporters in the two camps.

Resolving the disparity between these estimates is one of the goals of the new work by Yiqing Zhou, of the University of Illinois at Urbana–Champaign, and her two colleagues [1]. In their study, they focused on algorithms for classically replicating “imperfect” quantum computers, which are also known as NISQ (noisy intermediate-scale quantum) devices [4]. Today’s state-of-the-art quantum computers—including Sycamore—are NISQ devices. The algorithms the team used are based on so-called tensor network methods, specifically matrix product states (MPS), which are good for simulating noise and so are naturally suited for studying NISQ devices. MPS methods approximate low-entangled quantum states with simpler structures, so they provide a data-compression-like protocol that can make it less computationally expensive to classically simulate imperfect quantum computers (see Viewpoint: Pushing Tensor Networks to the Limit).

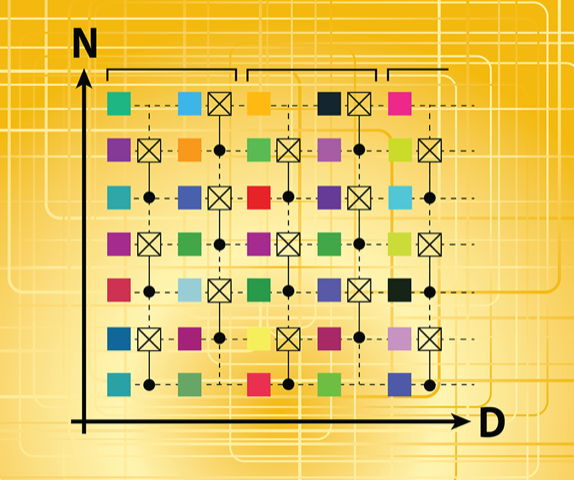
Zhou and colleagues first consider a random 1D quantum circuit made of neighboring, interleaved two-qubit gates and single-qubit random unitary operations. The two-qubit gates are either Controlled-NOT gates or Controlled-Z (CZ) gates, which create entanglement. They ran their algorithm for NISQ circuits containing different numbers of qubits, $N$ , and different depths, $D$ —a parameter that relates to the number of gates the circuit executes (Fig. 1). They also varied a parameter $𝜒$ in the MPS algorithm. $𝜒$ is the so-called bond dimension of the MPS and essentially controls how well the MPS capture entanglement between qubits.

The trio demonstrate that they can exactly simulate any imperfect quantum circuit if $D$ and $N$ are small enough and $𝜒$ is set to a value within reach of a classical computer. They can do that because shallow quantum circuits can only create a small amount of entanglement, which is fully captured by a moderate $𝜒$ . However, as $D$ increases, the team finds that $𝜒$ cannot capture all the entanglement. That means that they cannot exactly simulate the system, and errors start to accumulate. The team describes this mismatch between the quantum circuit and their classical simulations using a parameter that they call the two-qubit gate fidelity $f_{n}$ . They find that the fidelity of their simulations slowly drops, bottoming out at an asymptotic value $f_{\infty}$ as $D$ increases. This qualitative behavior persists for different values of $N$ and $𝜒$ . Also, while their algorithm does not explicitly account for all the error and decoherence mechanisms in real quantum computers, they show that it does produce quantum states of the same quality (perfection) as the experimental ones.

In light of Google’s quantum advantage claims, Zhou and colleagues also apply their algorithm to 2D quantum systems—Sycamore is built on a 2D chip. MPS are specifically designed for use in 1D systems, but the team uses well-known techniques to extend their algorithm to small 2D ones. They use their algorithm to simulate an $N = 54$ , $D = 20$ circuit, roughly matching the parameters of Sycamore (Sycamore has 54 qubits but one is unusable because of a defect). They replace Google’s more entangling “iSWAP” gates with less entangling CZ gates, which allow them to classically simulate the system up to the same fidelity as reported in Ref. [2] with a single laptop. The simulation cost should increase quadratically for iSWAP-gate circuits, and although the team proposes a method for performing such simulations, they have not yet carried them out because of the large computational cost it entails.

How do these results relate to the quantum advantage claims by Google? As they stand, they do not weaken or refute claims—with just a few more qubits, and an increase in $D$ or $f_{\infty}$ , the next generation of NISQ devices will certainly be much harder to simulate. The results also indicate that the team’s algorithm only works if the quantum computer is sufficiently imperfect—if it is almost perfect, their algorithm provides no speed up advantage. Finally, the results provide numerical insight into the values of $N$ , $D$ , $f_{\infty}$ , and $𝜒$ for which random quantum circuits are confined to a tiny corner of the exponentially large Hilbert space. These values give insight into how to quantify the capabilities of a quantum computer to generate entanglement as a function of $f_{\infty}$ , for example.

So, what’s next? One natural question is, Can the approach here be transferred to efficiently simulate other aspects of quantum computing, such as quantum error correction? The circuits the trio considered are essentially random, whereas quantum error correction circuits are more ordered by design [5]. That means that updates to the new algorithm are needed to study such systems. Despite this limitation, the future looks promising for the efficient simulation of imperfect quantum devices [6, 7].

References

Y. Zhou et al., “What limits the simulation of quantum computers?” Phys. Rev. X 10, 041038 (2020).
F. Arute et al., “Quantum supremacy using a programmable superconducting processor,” Nature 574, 505 (2019).
E. Pednault et al., “Leveraging secondary storage to simulate deep 54-qubit Sycamore circuits,” arXiv:1910.09534.
J. Preskill, “Quantum computing in the NISQ era and beyond,” Quantum 2, 79 (2018).
X. Gao and L. Duan, “Efficient classical simulation of noisy quantum computation,” arXiv:1810.03176.
S. Cheng et al., “Simulating noisy quantum circuits with matrix product density operators,” arXiv:2004.02388.
K. Noh et al., “Efficient classical simulation of noisy random quantum circuits in one dimension,” Quantum 4, 318 (2020).

About the Author

Jordi Tura is an assistant professor at the Lorentz Institute of the University of Leiden, Netherlands. He also leads the institute’s Applied Quantum Algorithms group. Tura obtained his B.Sc. degrees in mathematics and telecommunications and his M.Sc. in applied mathematics from the Polytechnic University of Catalonia, Spain. His Ph.D. was awarded by the Institute of Photonic Sciences, Spain. During his postdoctoral stay at the Max Planck Institute of Quantum Optics in Germany, Tura started working in the field of quantum information processing for near-term quantum devices.