Small Cavities Make Noisy Homes for Light

Gregory Moille; Kartik Srinivasan

Viewpoint

Small Cavities Make Noisy Homes for Light

Joint Quantum Institute, NIST/University of Maryland, College Park, MD, USA
National Institute of Standards and Technology, Gaithersburg, MD, USA

December 7, 2020• Physics 13, 192

Noise from temperature fluctuations may limit the performance of small optical cavities for quantum computing applications.

Figure caption — **Figure 1:** The photonic cavity shown here confines a light mode in a small space. In principle, achieving this confinement in ever smaller volumes would enable interesting nonlinear optical effects that are useful for quantum computing. But new work shows that thermal fluctuations in the device’s refractive index become more problematic in smaller devices, limiting how well light can be stored [1].

Lasers are everywhere from your cat’s toy box to an eye surgeon’s toolkit to your phone’s face-recognition hardware. The utility of lasers goes much further, and one particularly exciting application is nonlinear optical devices. When laser light enters a material, it can mix and produce a new beam that comprises, for instance, different colors or wavelengths. These effects require a high optical intensity (photon density), which can be achieved using an expensive high-powered laser. But another tack is to squeeze low-powered light into a small cavity that increases the photon density and confines the light for a long time. Thanks to improvements in fabrication, this latter approach has been successful, leading to applications of nonlinear effects in sensing, spectroscopy, and, potentially, quantum information. Shrinking the cavities further would therefore seem like a good way to enhance these nonlinear effects. Now, however, Christopher Panuski and colleagues from the Massachusetts Institute of Technology show that small-volume cavities may soon reach a size where thermal noise reduces the lifetime of the confined photons and limits performance [1].

Optical cavities, also known as optical resonators, are structures in which light is confined at specific (resonant) wavelengths that are dictated by the cavity geometry and material. Researchers have focused on improving two metrics that characterize light confinement in these devices [2]. The first is the quality factor (Q), which measures how long a resonant photon stays inside the cavity before it leaks out and should be as high as possible. The second is the cavity mode volume (V). V determines the light field’s spatial confinement and should be as small as possible. The intensity enhancement of light stored in the cavity is proportional to Q/V, with the best Q/V values reported today being about $1 0^{7}$ [3, 4].

Realizing high Q/V cavities is the primary way to decrease the requisite power for nonlinear optical phenomena; it’s also the way to potentially achieve nonlinearity with a single photon [5]. In such a system, a single photon could be enough to create a nonlinear effect that modifies the resonator’s quantum state, such as whether a resonant mode is occupied. This effect could then be used to perform a logical operation on photonic qubits. Achieving these operations at room temperature and in cavities that can be integrated into photonic circuits is being intensely pursued [6], and it would be a milestone for photon-based quantum computing.

Resonators of micrometer- or nanometer-sized dimensions are nearing the sort of Q/V value that’s desired for this application. But a crucial feature of some of the smallest resonators in use today is their susceptibility to thermorefractive (TR) fluctuations, where thermal noise causes the cavity’s refractive index to vary. Such changes in the index can alter the resonance wavelength that keeps light waves confined in the cavity. In large cavities, such as the interferometers used for gravitational-wave detection, researchers have assumed that the TR fluctuations have only a perturbative effect on the resonator. That is, they act as noise—an important issue for metrology applications—but they don’t impair the resonator’s ability to store light (Q). Whether the same hypothesis holds for resonators that are only a few nanometers in width is an open question. To date, experiments have only looked at the metrological impact of TR noise on these tiny resonators from the perspective, for example, of creating stable reference cavities and optical frequency combs [7]. Moreover, the small cavities studied in these experiments still had relatively large mode volumes (V) and were likely in the perturbative regime.

In their work, Panuski and colleagues explore TR noise in resonators with smaller mode volumes to see if it imposes a fundamental limit on Q/V [1]. The team derives equations that connect the light field in the resonator to a temperature variation in the cavity. (The model assumes that a small change of temperature leads to a correspondingly small change of the cavity’s refractive index.) In this way, they can calculate the spectral broadening of the resonance from TR noise and the corresponding limit in the storage time of cavity light. Their equations predict that TR noise should have a negligible effect on Q for large-mode-volume resonators, as expected, but it becomes an important effect for high-Q/V resonators with a sufficiently small mode volume.

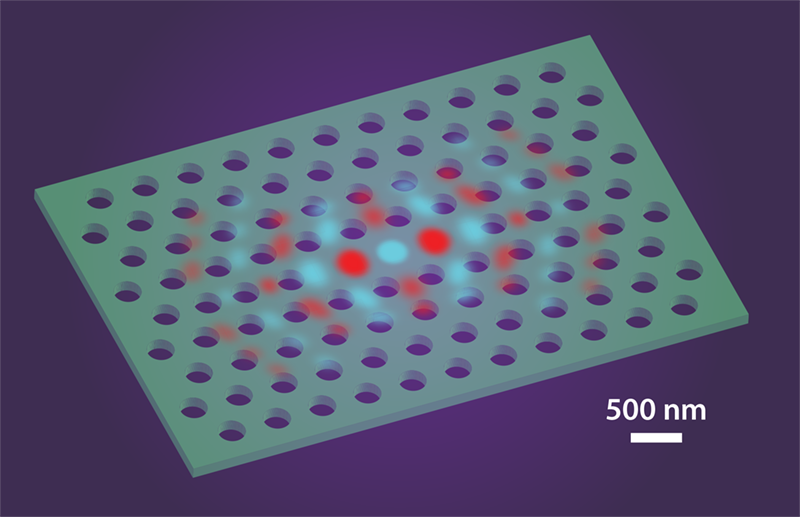
The researchers tested their model by performing sensitive measurements of TR noise in so-called photonic crystal cavities. In these slabs of high-index material (like silicon), a periodic arrangement of vertical air holes allows for confinement of light in a small space (Fig. 1). The team observes differences in TR noise for cavities with similar Q but different V, confirming their model predictions and the role of cavity size. Having validated their model, they employ it to predict the Q/V values where thermal noise impairs Q for cavities with different types of materials and cavity designs. Surprisingly, these fundamental limits are only about a factor of 10 greater than the Q/V numbers reported for existing devices. Examples of these “borderline” cases include silicon photonic crystals [3] and silica microtoroids [8].

The findings argue against the assumption that single-photon nonlinearities can be reached “simply” by boosting Q/V values through improved design and fabrication. Thermorefractive fluctuations can severely limit Q/V, so they have to be handled, or better, countered. In principle, there are paths to reducing the TR noise. These include working at cryogenic temperatures [9] or counterbalancing the TR noise of the cavity by cladding it with a material with the opposite thermorefractive response [10]. Another option, proposed by Panuski and colleagues, is to use the medium’s thermal expansion to counteract the thermorefractive effect. Yet all these approaches come with tradeoffs, such as technical complexity, the increase of other forms of noise, or design constraints. In the end, cryogenic operation may be the way to go because it’s already a necessity for another essential photonic system for quantum technologies; namely, single-photon detectors.

Beyond its importance for single-photon nonlinearities, Q/V is also a relevant metric for almost any cavity-enhanced light-matter interaction because it combines two key cavity effects—lengthened photon interaction times and increased electric-field intensity per photon. The results from Panuski and colleagues could thus have ramifications for applications that rely on cavity-enhanced interactions. Examples include systems that couple a cavity to a quantum dot or other atom-like object to create a high-brightness single-photon source, and experiments that use the cavity as a sensitive detector of single molecules as they transit through the cavity mode. In both cases, researchers may need to keep tabs on TR noise.

References

C. Panuski et al., “Fundamental thermal noise limits for optical microcavities,” Phys. Rev. X 10, 041046 (2020).
K. J. Vahala, “Optical microcavities,” Nature 424, 839 (2003).
T. Asano et al., “Photonic crystal nanocavity with a Q factor exceeding eleven million,” Opt. Express 25, 1769 (2017).
S. Hu et al., “Experimental realization of deep-subwavelength confinement in dielectric optical resonators,” Sci. Adv. 4, eaat2355 (2018).
D. E. Chang et al., “Quantum nonlinear optics — photon by photon,” Nat. Photon. 8, 685 (2014).
J. Lu et al., “Toward 1% single-photon anharmonicity with periodically poled lithium niobate microring resonators,” Optica 7, 1654 (2020).
T. Drake et al., “Thermal decoherence and laser cooling of Kerr-microresonator solitons (Conference Presentation),” Proc. SPIE 11298 Photonic Heat Engines: Science and Applications II 112980O (2020).
T. J. Kippenberg et al., “Demonstration of ultra-high-Q small mode volume toroid microcavities on a chip,” Appl. Phys. Lett. 85, 6113 (2004).
G. Moille et al., “Kerr-microresonator soliton frequency combs at cryogenic temperatures,” Phys. Rev. Applied 12, 034057 (2019).
Q. Zhao et al., “Low-loss low thermo-optic coefficient ${Ta}_{2} O_{5}$ on crystal quartz planar optical waveguides,” APL Photonics 5, 116103 (2020).

About the Authors

Gregory Moille is a postdoctoral researcher at the University of Maryland/NIST Joint Quantum Institute and NIST Physical Measurement Laboratory. He received his M.S. degree in physics and photonics from Grenoble Institut National Polytechnique in France, and received his Ph.D. in physics from Paris Saclay University. His main interests are in the study of chip-scale integrated microresonators for frequency comb applications.

Kartik Srinivasan is a scientist at NIST and the University of Maryland/NIST Joint Quantum Institute. He received B.S., M.S., and Ph.D. degrees in applied physics from the California Institute of Technology. His research activities have included work on integrated quantum photonics, quantum frequency conversion, nonlinear nanophotonics, nanoscale electro-optomechanical transducers, photonic crystals, and microresonator frequency combs. He is a Fellow of the Optical Society of America.