Physics Insights from Neural Networks
Machine-learning models based on neural networks are behind many recent technological advances, including high-accuracy translations of text and self-driving cars. They are also increasingly used by researchers to help solve physics problems [1]. Neural networks have identified new phases of matter (see Q&A: A Condensed Matter Theorist Embraces AI) [2], detected interesting outliers in data from high-energy physics experiments [3], and found astronomical objects known as gravitational lenses in maps of the night sky (see Q&A: Paving A Path for AI in Physics Research) [4]. But, while the results obtained by neural networks proliferate, the inner workings of this tool remain elusive, and it is often unclear exactly how the network processes information in order to solve a problem. Now a team at the Swiss Federal Institute of Technology (ETH) in Zurich has demonstrated a way to find this information [5]. Their method could be used by human scientists to see a problem—and a routing to solving it—in an entirely new way.
A neural network is a computational tool whose operation is loosely modeled on that of the human brain. The network typically consists of multiple layers of connected artificial neurons, which carry out calculations. The connections between neurons are weighted and those weights—which can number in the millions to billions—form the tunable parameters of the network. The beauty of neural networks lies in the fact that they don’t need to be programmed to solve a task. Rather, they learn by example, adjusting their parameters such that the solutions they output improve over time. For instance, to train a neural network to recognize a face, the network is given many different pictures of the same person. The network then learns to recognize this face—changing the weights of the connections until its “recognition quality” is sufficiently reliable. The trained network can then match other pictures to the same person without the user having to provide detailed information about specific characteristics of the person’s face.
While neural networks can learn to solve enormously diverse tasks, the inner workings of these models are often a black box. One way to understand what a network has learned is to look at its weights. But doing that is typically intractable because of their large number. This lack of understanding about how neural networks operate is particularly unsatisfying in physics: the tool can solve challenging problems, yet we do not know what rules and principles it used to produce the solutions. That is where the new result of Raban Iten, Tony Metger, and colleagues comes in [5].
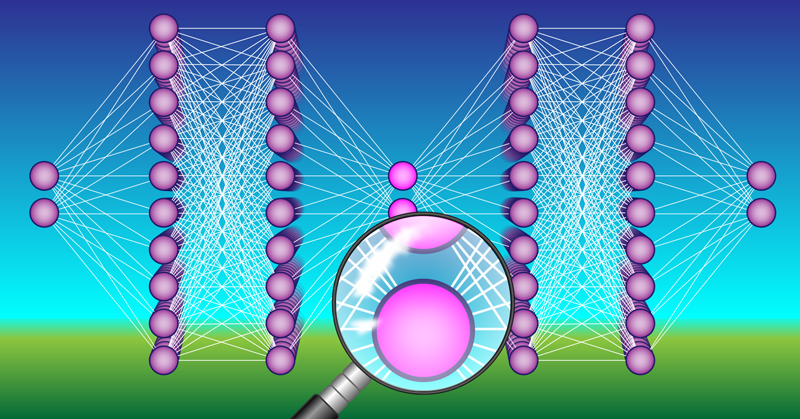
The team started out with a standard neural network made up of seven layers. They then modified the network in two crucial ways. First, they altered layer four—the middle layer of the network—so that it had fewer neurons than the other layers, creating a so-called information bottleneck. In one case, for example, they reduced the number of neurons this layer contained from 100 to 2 (Fig. 1). (The input and output layers for that case each also had two neurons). In other cases, the altered layer had more neurons, but the number was always less than 10. Second, they coded this altered layer so that each of its neurons contained independent information. The technique they adapted to do this coding is called disentanglement of variables and comes from the field of computer vision [6, 7]. Going back to the face recognition example, this modification means that one neuron in the altered layer might contain the shape of the mouth and another the size of the eyes. Together, the two modifications mean that the final neural network, which the team named SciNet, has a few-parameter layer in which each neuron contains information about an independent property of the problem being solved, making the network easier to study. It is this layer that the team probed to investigate the network’s internal workings.
To study the neural network, the team asked SciNet to solve different physics problems, the most representative being an astronomical one. For this problem, SciNet was given the angular coordinates of Mars and the Sun, which were measured from Earth with respect to some fixed stars. The neural network was then asked to predict the future positions of these celestial objects. After the training process, the team looked at the weights associated with the two neurons they had in layer four of the network to gain insight into how SciNet solved the task. By analyzing the outputs of the neurons in the middle layer, they found that SciNet performed a coordinate transformation, changing the angles of Mars so that they appeared to have been measured from the Sun rather than from Earth. That means, impressively, that SciNet switched from a geocentric to a heliocentric worldview, without explicitly being told to do so.
The demonstration by the ETH team allowed them to understand how the neural network solved a variety of specific tasks. But the result has wider importance. By understanding the inner workings of neural networks, physicists could use them to gain new insights and conceptual understanding of a problem—not just the final answer. For example, one could train SciNet to predict the outcomes of measurements of a quantum system to see how the network links the mathematical theory of quantum mechanics with reality. Another exciting opportunity for SciNet is studying the rotation curves of galaxies. Physicists still don’t understand why the stars in galaxies spin faster than predictions indicate they should for their visible mass, leading to the hypothesis that there is some unknown “dark matter” mass in the Universe. It would be fantastic to learn whether SciNet solves the problem by adding in hidden dark matter masses, modifying the laws of gravity, or using an entirely different representation, which astrophysicists could then interpret. SciNet’s answer could help point researchers in new directions to solve this long-standing, important problem.
This work therefore makes a step towards using machine-learning models as a source of inspiration in science, helping researchers find new ideas about physical problems and augmenting human creativity. Hopefully—in a few years, when these methods are better understood and are applied to unanswered scientific questions—they will lead to new conceptual understanding and thereby accelerate the progress of physics itself.
This research is published in Physical Review Letters.
References
- G. Carleo et al., “Machine learning and the physical sciences,” Rev. Mod. Phys. 91, 045002 (2019).
- J. Carrasquilla and R. G. Melko, “Machine learning phases of matter,” Nat. Phys. 13, 431 (2017).
- R. T. D’Agnolo and A. Wulzer, “Learning new physics from a machine,” Phys. Rev. D 99, 015014 (2019).
- Y. D. Hezaveh et al., “Fast automated analysis of strong gravitational lenses with convolutional neural networks,” Nature 548, 555 (2017).
- R. Iten et al., “Discovering physical concepts with neural networks,” Phys. Rev. Lett. 124, 010508 (2020).
- I. Higgins et al., “beta-VAE: Learning basic visual concepts with a constrained variational framework,” in Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 2017.
- T. Q. Chen et al., “Isolating sources of disentanglement in variational autoencoders,” in Advances in Neural Information Processing Systems 31 (NIPS 2018).