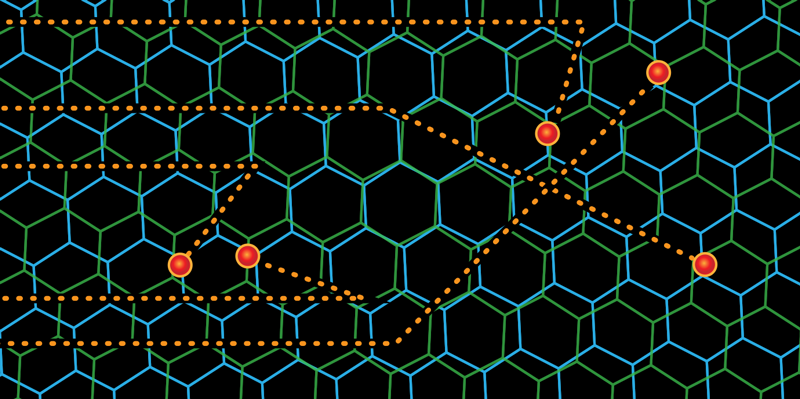
Graphene Reveals Its Strange Side

Subir Sachdev

Viewpoint

Graphene Reveals Its Strange Side

Department of Physics, Harvard University, Cambridge, MA, USA

February 18, 2020• Physics 13, 20

Experiments on magic-angle graphene reveal a “strange metal” phase and transport behavior consistent with so-called Planckian dissipation.

Figure caption — **Figure 1:** The resistivity of magic-angle graphene—under certain conditions—increases linearly with temperature. This “strange metal” behavior implies that the transport of electrons within the material is defined by a short scattering time that scales as the Planck constant divided by the temperature.

Magic-angle graphene captured the attention of condensed-matter physicists in 2018 when it was discovered that this material—made of two sheets of graphene with slightly misaligned lattice orientations (Fig. 1)—is a superconductor. Moreover, observations showed that the phase diagram of magic-angle graphene is similar to that of copper oxide high-temperature superconductors, with an insulating region next to a dome-shaped superconducting region (see Trend: Bilayer Graphene’s Wicked, Twisted Road). Now, Pablo Jarillo-Herrero from the Massachusetts Institute of Technology, Cambridge, and his colleagues report that magic-angle graphene has another remarkable feature of the cuprate phase diagram: a “strange metal” phase in which the resistivity scales linearly with temperature down to very low temperatures [1]. This temperature dependence is unlike that of most metals and has proved difficult to explain with traditional models of electron conduction. The one clue that theorists have is that the strange metal phase is associated with a low-temperature transport behavior called Planckian dissipation [2, 3]. The same association is found by Jarillo-Herrero and colleagues in magic-angle graphene, providing further evidence that strange metals are united by a fundamentally new form of transport that theorists are busy trying to characterize.

The transport of electrical and heat currents in metals was once a well-understood corner of condensed-matter physics. This understanding was based on the Drude formula, which relates the electrical conductivity to the density of mobile electrons, the mass of an electron, and the time between scattering events, $𝜏$ . The original theory, developed by Paul Drude in 1900, treated the electrons as classical particles and largely ignored electron-electron interactions. Remarkably, Drude’s formula survived a quantum-mechanics update in the 1930s, in which the electron mass was replaced by the effective mass of an electronic “quasiparticle,” and the scattering time was reformulated with a low-temperature divergence of $𝜏 \sim T^{- 2}$ , which is the expected behavior for quasiparticle scattering. With these additions, the Drude formula described metallic transport with unalloyed success until the mid 1980s.

This comfortable situation changed soon after the discovery of high-temperature superconductivity in the cuprate compounds in 1986. In the cuprate phase diagram—at temperatures above the superconducting “dome”—researchers identified a strange metal phase in which the resistivity is proportional to the temperature. This linear behavior implied that the scattering time scales as $𝜏 \sim T^{- 1}$ , which conflicts with expectations from the Drude formula. The experiments by Jarillo-Herrero and colleagues have shown that magic-angle graphene also exhibits this strange metal phase [1]. The team utilized several samples of magic-angle graphene and measured the resistivity at various temperatures and charge-carrier densities. One of the advantages of working with graphene is that the carrier density can be tuned fairly easily with a gate voltage, as opposed to other materials that require doping. The researchers observed a linear temperature dependence in the resistivity above temperatures of around 1 K.

Finding another strange metal in magic-angle graphene puts new pressure on theorists to come up with an explanation for this phenomenon. Despite several efforts to explain the linear temperature dependence within the Drude model, it has become clear that the quasiparticle description fails in the strange metal regime. Much theoretical work has been directed towards finding a new paradigm of transport in which charge and heat are carried not by particle-like “lumps,” but collectively by a many-body state that connects a large number of particles through long-range quantum entanglement.

This effort in many-body physics has been guided by a key observation. In 2013, experimentalists uncovered a universal behavior in strange metals by converting the observed resistivity to a scattering time $𝜏$ using the familiar Drude formula [2], even though there is little theoretical justification for employing a formula derived from the quasiparticle theory. Upon examining a large number of strange metals, they found a remarkable result: $𝜏 = C ℏ ∕ k T$ , where $C$ is a dimensionless constant, $ℏ$ is the Planck constant, and $k$ is the Boltzmann constant. Across a wide range of strange metals, $C$ is close to unity [3]. And now magic-angle graphene can be added to this list, as Jarillo-Herrero’s team reports similar values of $C$ [1]. This universality is surprising, as we would expect a large variation in $C$ for different materials. The reasoning is that the scattering time is thought to be inversely proportional to the strength of electron-electron interactions, and these interactions are very different for cuprates, magic-angle graphene, and other strange metals. The actual situation—in which the scattering time for strange metals is uniform and relatively short compared to other materials—has been characterized as “Planckian dissipation” [3].

A description of nonquasiparticle transport and Planckian dissipation in metals remains a challenge. Significant progress has been made recently using the Sachdev-Ye-Kitaev (SYK) model, which describes an island of electrons with random and all-to-all interactions. A single SYK island exhibits nonquasiparticle excitations and Planckian dissipation, and recent attempts to place many of these islands within a lattice framework have shown some promise in modeling strange metal transport [4]. But the connection of such models to the microscopic degrees of freedom in real-world strange metals remains unclear and is the focus of current research.

One possible direction for tying SYK models to strange metals is through an emerging connection between theories of many-body quantum chaos and Planckian dissipation. Recent work has found an upper bound on the growth rate of chaos in a broad class of systems [5]. The upper bound is saturated by the growth of chaotic behavior within the SYK model. An interesting open question is whether the chaos parameters—such as the “butterfly velocity” that describes how chaos spreads out spatially from an initial quantum state—can be related to transport coefficients. Such a link could help better understand the universality of the observed Planckian behavior.

Another related direction for the study of Planckian dissipation is with black holes. When disturbed by an external perturbation, black holes oscillate before returning to a stationary state. The decay time of the oscillation modes is of order the Planckian time $ℏ ∕ k T$ , where $T$ is the Hawking temperature of the black hole. This feature of black holes is not entirely unexpected, as the anti-de Sitter/conformal field theory correspondence of string theory [6] relates a quantum black hole to strongly interacting relativistic field theories, which are known to exhibit Planckian dissipation. Recent work has further shown that the SYK model has a connection to charged black holes [7]. For these reasons, theorists have added gravitational theory methods to their toolbox for studying Planckian dissipation in condensed-matter systems.

This research is published in Physical Review Letters.

References

Y. Cao et al., “Strange metal in magic-angle graphene with near Planckian dissipation,” Phys. Rev. Lett. 124, 076801 (2020).
J. A. N. Bruin et al., “Similarity of scattering rates in metals showing t-linear resistivity,” Science 339, 804 (2013).
A. Legros et al., “Universal T-linear resistivity and Planckian dissipation in overdoped cuprates,” Nat. Phys. 15, 142 (2018).
X.-Y. Song et al., “Strongly correlated metal built from Sachdev-Ye-Kitaev models,” Phys. Rev. Lett. 119, 216601 (2017).
J. M. Maldacena et al., “A bound on chaos,” J. High Energy Phys. 2016, 106 (2016).
J. M. Maldacena, “The large N limit of superconformal field theories and supergravity,” Adv. Theor. Math. Phys. 2, 231 (1998).
S. Sachdev, “Universal low temperature theory of charged black holes with ${AdS}_{2}$ horizons,” J. Math. Phys 60, 052303 (2019).

About the Author

Subir Sachdev studied at the Indian Institute of Technology in Delhi, the Massachusetts Institute of Technology (MIT), and Harvard University. He is now the Herchel Smith Professor of Physics and department chair of physics at Harvard University. He has been elected to academies of science in the United States and India. Sachdev has received several honors, including the APS LeRoy Apker Award (1983) for his work as an undergraduate at MIT, the APS Lars Onsager Prize (2018), and the Dirac Medal (2018). In 2009 he was recognized as an Outstanding Referee by the American Physical Society.