Spin Control with a Topological Semimetal
Topological materials, from graphene to topological insulators, owe their remarkable properties to their two-dimensional surface states, which are protected from disorder and defects by topology and symmetry. A recently discovered class of materials, known as topological semimetals, often exhibit even richer and more robust topological effects. These materials include Dirac semimetals (DSMs) and Weyl semimetals (WSMs) [1, 2], which host electronic excitations behaving like Dirac and Weyl fermions, respectively. One of their intriguing properties is that the spins and momenta of their surface electrons are “locked.” Loosely speaking, this means that right-moving electrons are spin-up polarized, while left-moving ones are spin-down polarized—a behavior that can lead to exotic physics and may be harnessed in spintronic devices. However, it has been challenging to observe spin-polarized currents in these semimetals, mostly because currents are carried by both surface and bulk electrons, and spin-momentum locking isn’t as strong in the latter. Now, a team led by Zhi-Min Liao of Peking University has demonstrated a clever setup that reveals, with simple electrical measurements, spin-polarized transport in a DSM nanowire [3]. The researchers say that the setup can single out the contribution of surface electrons, eliminating that of bulk electrons. What’s more, the configuration allows the spin-polarized signal to be turned on and off with an applied voltage.
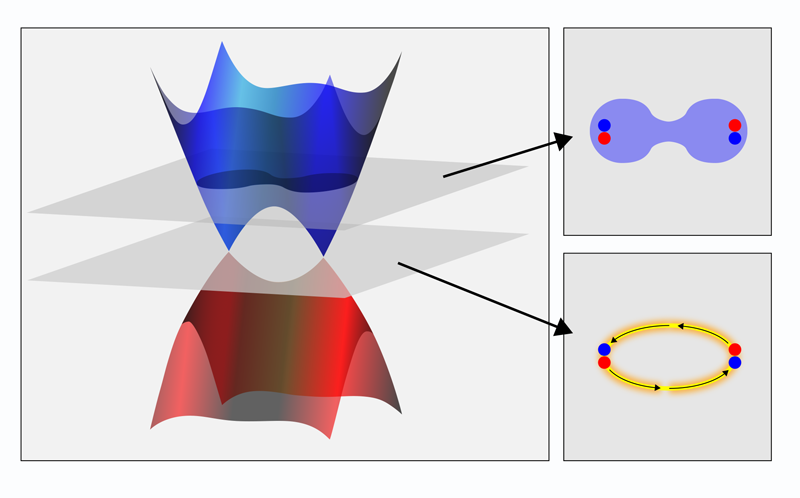
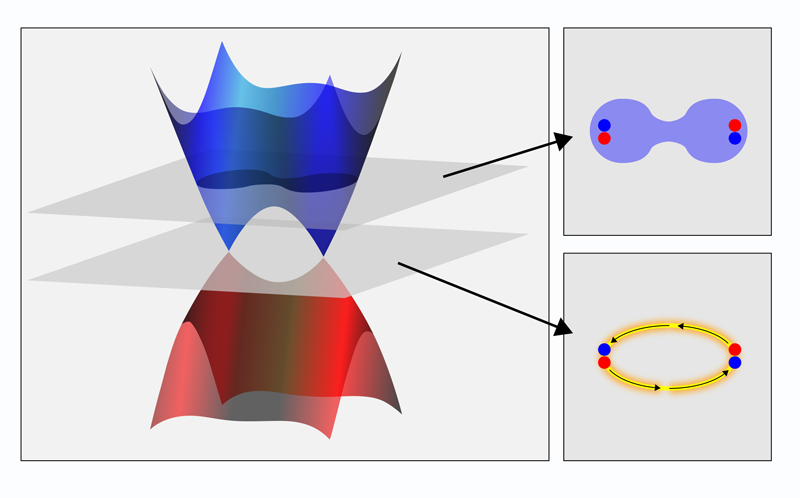
The properties of a topological material are related to its unique electronic band structure, which represents the allowed energy levels as a function of momentum for electrons moving in the solid. In two-dimensional graphene and on the surfaces of topological insulators, valence and conduction bands can be described as pairs of Dirac cones—each of which is like a stalactite meeting a stalagmite. The two cones meet at so-called Dirac points with a vanishing energy gap between them. Topological semimetals, which are three dimensional, have more complex band structures. In Weyl semimetals (like TaAs and WTe2) and Dirac semimetals (like Na3Bi or Cd3As2), Dirac bands can appear in multiple copies, with several stalactite-stalagmite pairs meeting at the same or nearby Dirac points (Fig. 1). The Dirac points of neighboring pairs are connected by arc-shaped partial Fermi surfaces called Fermi arcs [4], which describe the characteristic surface electronic states of these materials. In fact, the observation of these arcs in photoemission experiments provided the smoking gun for the long-sought-after topological semimetals.
According to theory, Fermi-arc states should exhibit spin-momentum locking—a property that would offer thrilling new perspectives for the development of spintronic devices, which rely on the creation and manipulation of spin-polarized electron currents. This property has been verified by photoemission measurements, which characterize Fermi-arc electrons under equilibrium condition. However, experiments have not yet fully characterized the nonequilibrium conditions that would be relevant for devices: the dynamic transport of spin and charges associated with net spin-polarized currents. While recent studies have seen some signatures of spin-polarized transport [5], the evidence remains scarce. What complicates these experiments is the fact that, in topological semimetals, both bulk and surface states are metallic and thus contribute to transport.
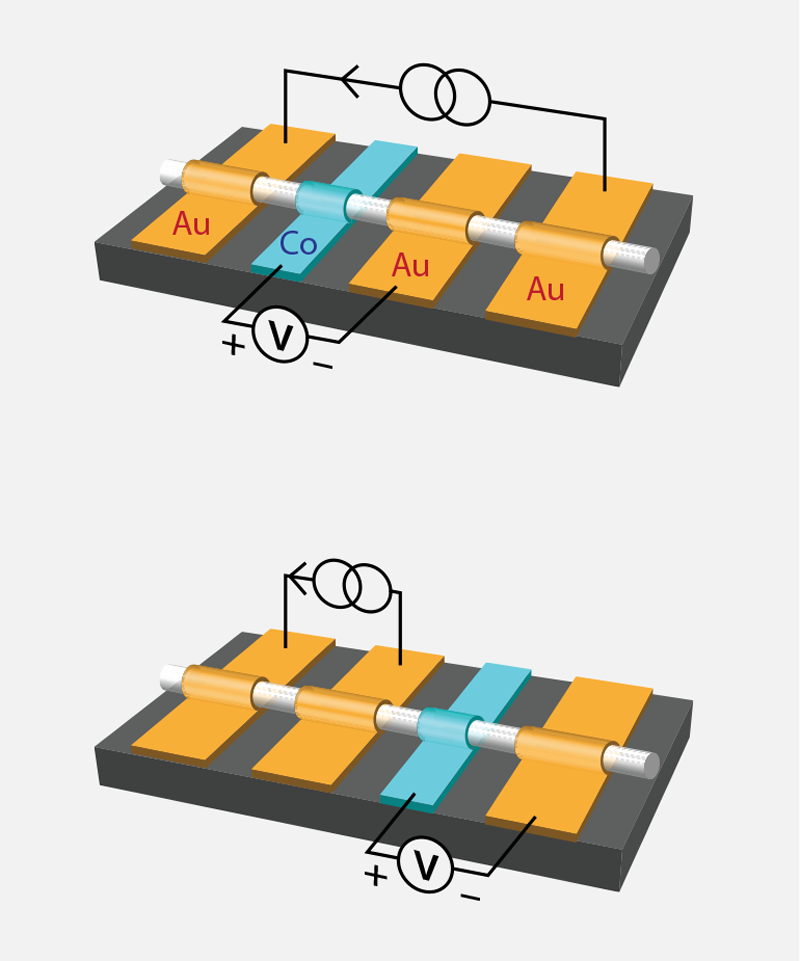
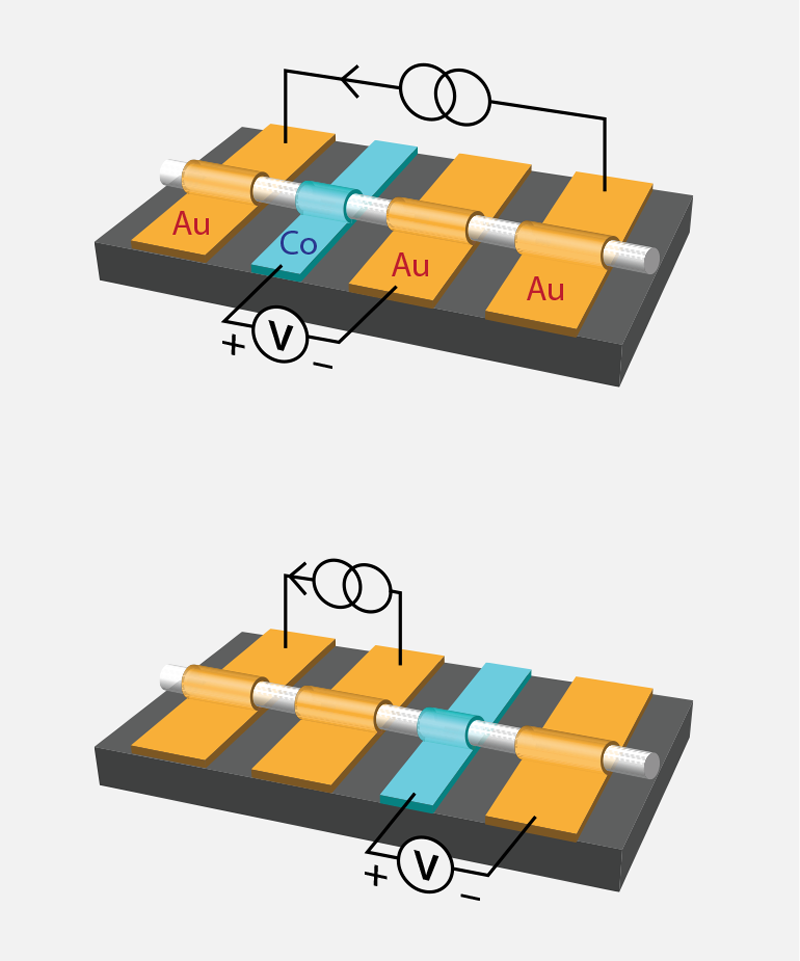
Liao and his co-workers study the spin-momentum locking property of DSM surface electrons using a nanowire made of a DSM (Cd3As2) connected to four electrodes. In the first configuration (Fig 2, top), two outer electrodes inject a current into the nanowire, and two inner electrodes, placed in the path of the current, measure the voltage across two points of the wire. One of these inner electrodes is made of cobalt (Co), which can be magnetized in a direction perpendicular to the wire by an applied magnetic field. Because of the Co magnetization, a current of electrons with a preferential spin orientation would produce a negative or positive voltage due to spin-momentum locking depending on whether the spin is parallel or antiparallel to the magnetization direction. By flipping the direction of the current or of the magnetization, the sign of the detected voltage should flip. This is exactly what the researchers observe. Together with the observation of hysteretic behavior in the voltage-vs-magnetic field curve, this spin-flipping effect, which is similar to that previously reported [5], clearly reveals the spin-polarization of the Fermi-arc current. However, these “local” measurements—in which the voltage is measured along the path of the current—include bulk contributions as well.
To eliminate such contributions, the Peking team set up an additional, “nonlocal,” configuration, in which a current is injected between two gold electrodes on one side of the wire, and a spin-voltage is detected by the Co-Au electrode pair on the other side of the sample (Fig 2, bottom). The researchers suggest that, instead of being driven by the current, electrons diffuse through the wire from the injection to the detection electrodes, regardless of the current direction. They argue that only the strongly spin-locked surface states, but not the bulk states, can generate such a diffusion-driven spin voltage in this nonlocal configuration. Their interpretation is supported by the fact that the sign of the voltage is, unlike in the local measurement, independent of current polarity.
The setup also allowed the team to carry out a third type of measurement, in which they applied a “gate” voltage between the wire and the underlying substrate. This voltage causes the Fermi surfaces of separate Dirac cones to climb up in energy, so that the projected Weyl points become more closely spaced and the Fermi arcs shrink. At a sufficiently large voltage, a so-called Lifschitz transition occurs: The Fermi level passes the ceiling of two neighboring Dirac cones, and the material transitions from a DSM to a conventional metallic state, in which spin-momentum locking is lost (Fig. 1). At that point, the spin signal vanishes.
Taken together, the experiments deliver a clear picture of the highly spin-polarized currents derived from the spin-momentum locking in the Fermi-arc state of a DSM. The possibility to control the spin current with a voltage suggests that the configuration could serve as a switch for spin-polarized currents. However, the voltage needed to drive the Lifshitz transition in the researchers’ single-gate scheme exceeds 10 V—too large for practical devices. In this context, topological protection is a double-edged sword, leading to a robust effect that, unfortunately, cannot be controlled without overcoming a large energy barrier. There may be ways to mitigate this problem with split gates that can align and misalign different parts of the Dirac cones independently. The application of this split-gate approach to graphene led to the design of a so-called Klein tunnel transistor [6, 7], providing a way to modulate graphene’s ultrahigh mobilities with modest voltages ( [TeX:] $\sim 1$– [TeX:] $2$ V), with potential applications in high-speed analog devices [8]. Split-gate schemes may also be used to apply bi-directional torques to efficiently write information onto magnetic memory bits, as shown recently for 3D topological insulators [9].
This research is published in Physical Review Letters.
References
- A. M. Turner and A. Vishwanath, “Beyond band Insulators: Topology of semimetals and interacting phases,” Contemporary Concepts of Condensed Matter Science 6, 293 (2013).
- A. Vishwanath, “Where the Weyl things are,” Physics 8, 84 (2015).
- B.-C. Lin et al., “Electric control of Fermi arc spin transport in individual topological semimetal nanowires,” Phys. Rev. Lett. 124, 116802 (2020).
- S.-Y. Xu et al., “Discovery of a Weyl fermion semimetal and topological Fermi arcs,” Science 349, 613 (2015).
- P. Li et al., “Spin-momentum locking and spin-orbit torques in magnetic nano-heterojunctions composed of Weyl semimetal WTe2,” Nat. Commun. 9, 3990 (2018).
- R. N. Sajjad and A. W. Ghosh, “Manipulating chiral transmission by gate geometry: Switching in graphene with transmission gaps,” ACS Nano 7, 9808 (2013).
- K. Wang et al., “Graphene transistor based on tunable Dirac fermion optics,” Proc. Natl. Acad. Sci. U.S.A. 116, 6575 (2019).
- Y. Tan et al., “Graphene Klein tunnel transistors for high speed analog RF applications,” Sci. Rep. 7, 9714 (2017).
- K. M. Masum Habib et al., “Chiral tunneling of topological states: Towards the efficient generation of spin current using spin-momentum locking,” Phys. Rev. Lett. 114, 176801 (2015).