Theory for Polar Dielectrics Goes Nonlocal
As the field of nanophotonics emerged in the 80s, it brought together two seemingly irreconcilable realms—optics and nanotechnology. Naively, diffraction effects should make it impossible to exert nanometer-scale control on light with micrometer wavelengths. Nevertheless, nanophotonics has grown into a mature research field, thanks to approaches that overcome the diffraction limit by coupling light to small apertures, sharp tips, and other nanoscale objects [1]. Developing theories for nanophotonics systems is, however, challenging because they have to capture both the macroscopic scales relevant for optical phenomena and the atomic scales relevant for nanoscale effects. One problem is that conventional electromagnetic theories assume that the electrical polarization at a given point inside a material only depends on the electric field at the same point—a “local” assumption that is known to fail in some nanostructures. Now, Christopher Gubbin and Simone De Liberato of the University of Southampton in the UK have developed a nonlocal theory applicable to polar dielectrics, materials that hold tremendous potential for nanophotonics applications at infrared wavelengths [2]. Through a comparison with previous experiments, the researchers show that their theory can successfully describe the rich nonlocal phenomenology of nanostructures made of these materials.
One of the most successful strategies in nanophotonics has involved coupling photons and material excitations, or quasiparticles, to yield mixed states called polaritons. The great advantage of these hybrid states is that they can be tuned through their light and matter contents. Loosely speaking, one can adjust the light component to make polaritons delocalized and coherent, so that they are able to transport information over a large distance. And one can tune their matter component so that they can be confined to the nanoscale and interact with each other.
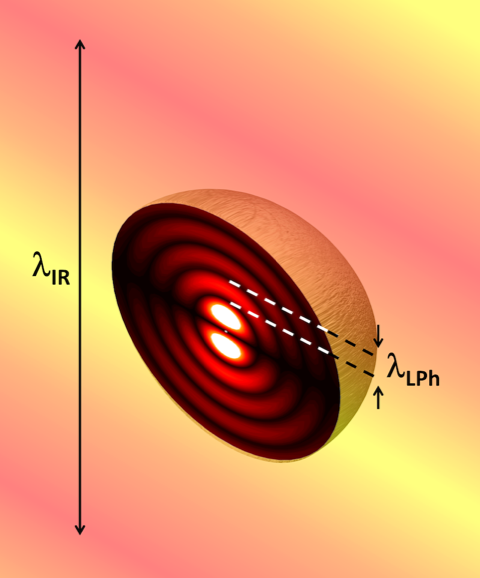
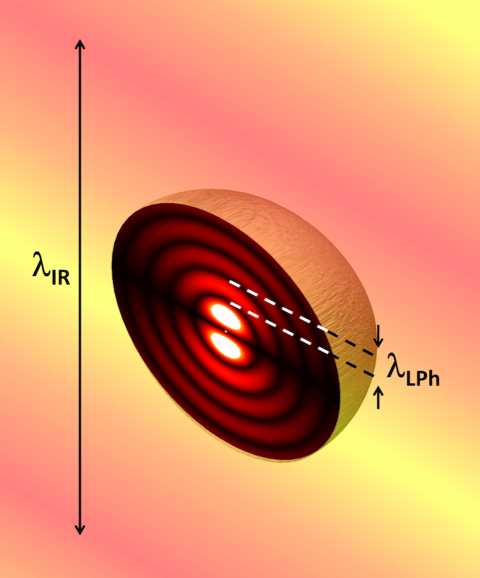
Depending on the material, the formation of polaritons involves different quasiparticles. In the case of metals, the quasiparticles are collective excitations of the electronic plasma called plasmons. The merging of photons and plasmons produces surface plasmon polaritons. In polar dielectrics—crystal semiconductors formed by molecules with a permanent dipole moment—the quasiparticles are collective vibrations of the crystal lattice, known as optical phonons. The merging of photons and phonons produces surface phonon polaritons, whose wavelengths lie in the infrared range of the electromagnetic spectrum ( – ). At these wavelengths, phonon polaritons feature an optimal balance between light concentration and low-loss propagation. This property has attracted much interest in areas such as molecular spectroscopy [3], superresolution lithography [4] or super-Planckian heat transfer [5].
To fully harness the technological potential of surface phonon polaritons, researchers need a more accurate description than that achievable with local Maxwell’s equations. Previous research on plasmonic metallic nanostructures has demonstrated the key role played by nonlocal effects. In particular, experiments [6] showed that light can excite longitudinal plasmon oscillations, whose coupling to light can only be explained with nonlocal calculations [7]. In metallic nanostructures, ignoring nonlocal effects would lead to erroneous predictions of important properties like the achievable light confinement. However, the impact of nonlocality on dielectric nanostructures hosting phonon polaritons has so far been neglected, even though experiments have revealed similar longitudinal-mode excitations in these materials [8].
Gubbin and De Liberato have now developed a nonlocal model for the infrared response of polar dielectrics. The nonlocality originates from electromagnetic constitutive relations in which the electric displacement field (accounting for the electrical polarization) at one point depends on the electric field within a finite volume around that point. As a result, the dielectric function, which relates the displacement field to the electric field, does not depend only on the electromagnetic field’s frequency but also on its wave vector. This dependence affects the interaction of light and matter in these materials. Specifically, it allows the coupling of photons not only to transverse optical phonons—lattice vibrations in which atoms move perpendicularly to the photon propagation direction—but also to longitudinal phonons, in which atoms oscillate along the propagation direction. The researchers show that this mechanism becomes relevant in few-nanometer-sized structures, in which radiation can couple to electromagnetic-field components with extremely large wave vectors (Fig. 1).
Gubbin and De Liberato find that nonlocality has a remarkably different impact on polar dielectrics than on metals. Surprisingly, nonlocality seems to be more pronounced in dielectrics (where electrons are bound to the atoms) than in metals (where electrons are quasifree). Compared to plasmons in metals [9], longitudinal phonon resonances in polar dielectrics are closer in energy to surface polaritons, and thus the phonon-polariton interactions affect the whole infrared range of the spectrum. What’s more, nonlocality becomes evident only for very small (0.1 nm) metallic structures, but it appears in dielectric structures as large as 10 nm.
To illustrate the power of their nonlocal theory, Gubbin and De Liberato apply it to calculate different optical properties—like scattering and extinction spectra—for two types of polar dielectric nanostructures: silicon carbide nanospheres and nanometer-thin films of aluminium nitride (AlN). The results reveal a diversity of nonlocal effects, including shifts and broadening of optical resonances due to the size-dependence of the phonon-polariton interaction. Importantly, the nonlocal theory provides a good fit to available experimental data on AlN films [10].
The result is a significant step forward in the fundamental description of polar dielectric nanostructures and may open new avenues for designing nanophotonic devices exploiting phonon polaritons. The improved theory may, for example, guide the development of schemes similar to that investigated in Ref. [8], which aim at the all-electrical control of infrared light. The theory may also help researchers develop sensing, imaging, and spectroscopy applications that exploit subtle shifts in polariton resonances caused by environmental, electromagnetic, and geometrical factors. As Gubbin and De Liberato show, a nonlocal theory is needed to reliably interpret the positions of these resonances. Finally, the new work is relevant for novel phonon-polaritonic materials, such as atomically thin van der Waals crystals and heterostructures, which are recently receiving a lot of attention [11]. Is it possible that the emergence of optical nonlocality in these systems has been overlooked so far?
This research is published in Physical Review X.
References
- L. Novotny and B. Hetch, Principles of Nano-Optics (Cambridge University Press, Cambridge, 2012)[Amazon][WorldCat].
- C. R. Gubbin and S. De Liberato, “Optical nonlocality in polar dielectrics,” Phys. Rev. X 10, 021027 (2020).
- M. Autore et al., “Boron nitride nanoresonators for phonon-enhanced molecular vibrational spectroscopy at the strong coupling limit,” Light Sci. Appl. 7, 17172 (2017).
- P. Li et al., “Reversible optical switching of highly confined phonon–polaritons with an ultrathin phase-change material,” Nat. Mater. 15, 870 (2016).
- B. Song et al., “Enhancement of near-field radiative heat transfer using polar dielectric thin films,” Nat. Nanotechnol. 10, 253 (2015).
- C. Ciraci et al., “Probing the ultimate limits of plasmonic enhancement,” Science 337, 1072 (2012).
- A. I. Fernández-Domínguez et al., “Transformation-optics description of nonlocal effects in plasmonic nanostructures,” Phys. Rev. Lett. 108, 106802 (2012).
- A. D. Dunkelberger et al., “Active tuning of surface phonon polariton resonances via carrier photoinjection,” Nat. Photon. 12, 50 (2017).
- S. Raza et al., “Unusual resonances in nanoplasmonic structures due to nonlocal response,” Phys. Rev. B 84, 121412 (2011).
- D. C. Ratchford et al., “Controlling the infrared dielectric function through atomic-scale heterostructures,” ACS Nano 13, 6730 (2019).
- N. Rivera et al., “Phonon polaritonics in two-dimensional materials,” Nano Lett. 19, 2653 (2019).