Connecting Qubits with a Topological Waveguide
Recognizing the role of topology in physics has led to breakthroughs in fields ranging from quantum materials to acoustics [1, 2]. Recently, researchers have shown that the topology of a photonic system is a powerful lever for manipulating light, opening the door to the realization of devices such as nanoscale lasers and defect-insensitive frequency converters [3]. Now, Eunjong Kim and Xueyue Zhang, both of the California Institute of Technology, and colleagues have explored how topology can endow special properties to a photonic platform in which superconducting qubits are embedded in a waveguide [4]. The researchers show that this configuration produces topological states in the waveguide and observe an imprint of this topological behavior in a directional coupling between qubits. The coherent transfer of the state of one qubit to the other via the topological states also suggests that the scheme might have potential in quantum information.
The first observed topological phenomenon was the integer quantum Hall effect, which occurs when electrons confined to two dimensions are exposed to a high magnetic field [5]. At certain field values, the bulk becomes an insulator, but the material’s electrical resistance vanishes. The apparent paradox of a conductive insulator is explained by the emergence of a conducting, or gapless, one-dimensional “edge” state at the interface between the topological bulk and the surrounding vacuum, which has a normal, or “trivial,” topology. Similar gapless states have since been observed in other electronic systems (1D, 2D, and 3D) wherever there is a boundary between regions with distinct topology.
Topological behavior, however, isn’t limited to electronic systems. It can emerge in any system with a band structure, such as photons moving in periodic structures. The realization that many models for electronic systems have analogous photonic counterparts drove tremendous progress in creating topological photonic materials [4]. Perhaps the simplest topological model amenable to a photonic extension is the Su-Schrieffer-Heeger (SSH) model, which describes spinless quantum particles hopping between sites in a one-dimensional lattice [6]. Each unit cell of the lattice has two sites, A and B, and particles can hop between sites either within a given unit cell or across neighboring cells. If the probability of hopping across neighboring cells is larger than that of hopping within a unit cell, a topological phase emerges. In this phase, the edge states are point-like, or quasi-zero-dimensional, modes that live at the ends of the chain. These edge states have remarkable properties: The wave function of each edge state extends in only one direction and is nonzero on only one of the two sublattices, A or B.
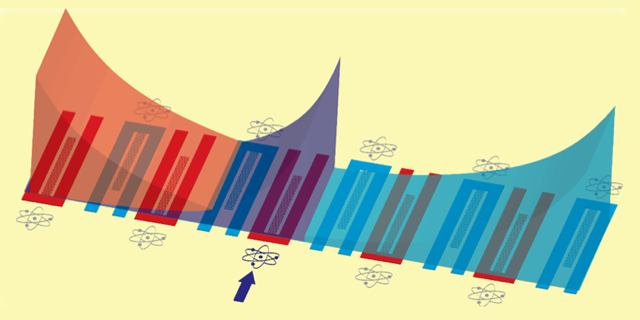
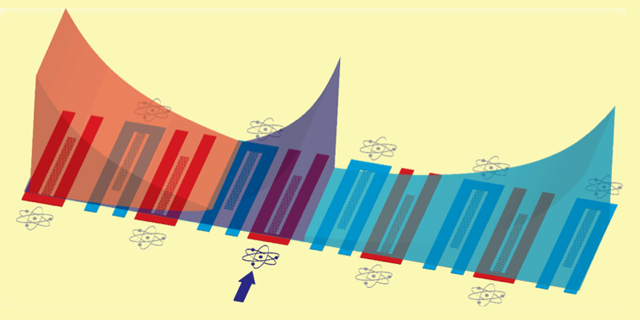
Following a recent proposal [7], Kim and colleagues built a system in which quantum emitters—superconducting qubits—are connected through a waveguide analogous to a topological SSH array (Fig. 1): The waveguide is a linear chain of identical microwave resonators paired to form an A-B lattice. Each resonator is a “site,” and the resonator-to-resonator coupling allows photons to hop between sites. By fabricating different waveguides with varying distances between resonators, the team tuned the coupling between sites, switching the band structure of the waveguide between trivial and topological. Measurement of the waveguide transmission spectra allowed the researchers to observe the signature of the topological transition. For the trivial case, a spectral gap, or band gap, appeared, in which transmission was blocked. When the system became topological, a transmission peak appeared within the band gap.
The team complemented the waveguide with superconducting qubits embedded at each lattice site, using techniques borrowed from circuit quantum electrodynamics [8]. The qubits, whose photon-emission frequencies are tunable, interact with the photonic states of the waveguide. When a qubit’s frequency falls within the band gap, there are no propagating modes to which the quibit excitation can couple. As a result, the excitation creates a “bound state” that remains localized around the qubit (Fig. 1). In a typical waveguide, this excitation would be symmetrical, extending on either side of the qubit. For the topological waveguide, the bound states inherit the directionality from the SSH lattice, extending in one direction and on one sublattice only.
These properties provide the possibility of engineering directional coupling between the qubits, which the researchers demonstrated by measuring energy-level splittings as qubits were tuned in and out of resonance with each other. These measurements show that qubit-induced bound states extend in only one direction and couple to only one sublattice.
The team demonstrated that they could harness the directional coupling enabled by topology by performing a coherent state transfer between two qubits that would otherwise be uncoupled. Within the qubit chain, they picked two qubits whose bound states faced away from each other and as such had no direct overlap. The transfer, however, was mediated by the small coupling between the edge states of the array. This state transfer occurred with reasonably high fidelity, but even better fidelity could be achieved by modifying the scheme so that the interaction between the qubits and the edge states could be appropriately tuned and timed.
This work opens the door to a number of enticing applications. Remaining in 1D, longer chains can be used to more thoroughly explore exotic many-body states, such as an ordered state called the double Nèel phase. Without topological bands, generating this phase would entail the complication of using a frustrated lattice [8]. Furthermore, by introducing tunable coupling between the resonators, researchers could build a powerful quantum simulator able to explore a wide parameter space of the SSH model. Achieving simultaneous, identical tuning of many couplers, however, is a significant technological challenge.
The 1D concept may also be extended to higher dimensions. To address and control a 2D array of qubits and resonators will require the engineering of complex 3D integrated circuits with multiple stacked chips [9]. But the payoff would be a set of photonic materials that provide a rich playground for fundamental and applied studies relevant to condensed-matter physics, materials science, quantum simulation, and quantum information. For instance, a 2D topological photonic array coupled to quantum emitters would enable the study of many-body states that include fractional quantum Hall analogs, photonic equivalents of Weyl and Dirac semimetals, and symmetry-protected quantum phases [10].
References
- M. Z. Hasan, and C. L. Kane, “Colloquium: Topological insulators,” Rev. Mod. Phys. 82, 3045 (2010).
- S. A. Cummer et al., “Controlling sound with acoustic metamaterials,” Nat. Rev. Mater. 1, 16001 (2016).
- T. Ozawa et al., “Topological photonics,” Rev. Mod. Phys. 91, 015006 (2019).
- E. Kim et al., “Quantum electrodynamics in a topological waveguide,” Phys. Rev. X 11, 011015 (2021).
- K. von Klitzing et al., “New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance,” Phys. Rev. Lett. 45, 494 (1980).
- K. Asbóth et al., A Short Course on Topological Insulators, Lecture Notes in Physics (Springer, New York, 2016)[Amazon][WorldCat].
- M. Bello et al., “Unconventional quantum optics in topological waveguide QED,” Sci. Adv. 5, eaaw0297 (2019).
- M. Kjaergaard et al., “Superconducting qubits: Current state of play,” Annu. Rev. Condens. Matter 11, 369 (2020).
- D. Rosenberg et al., “3D integrated superconducting qubits,” npj Quantum Inf. 3, 42 (2017).
- I. Carusotto et al., “Photonic materials in circuit quantum electrodynamics,” Nat. Phys. 16, 268 (2020).