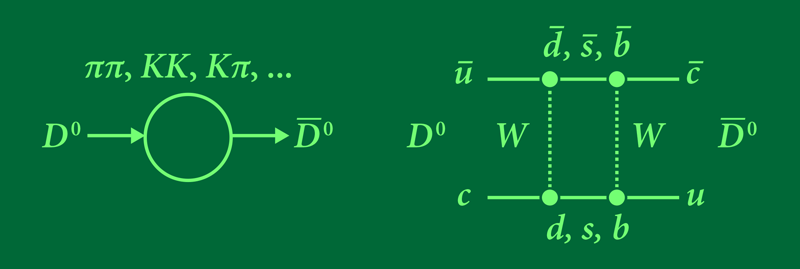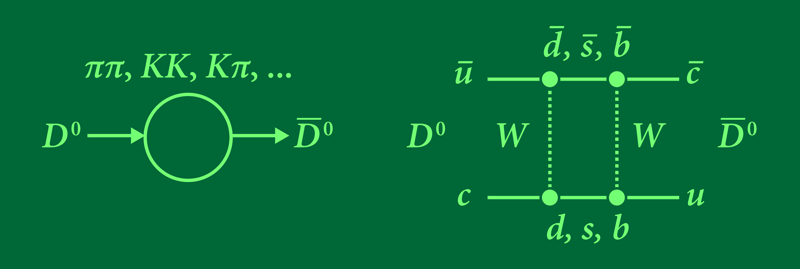Unraveling D-Meson Mixing
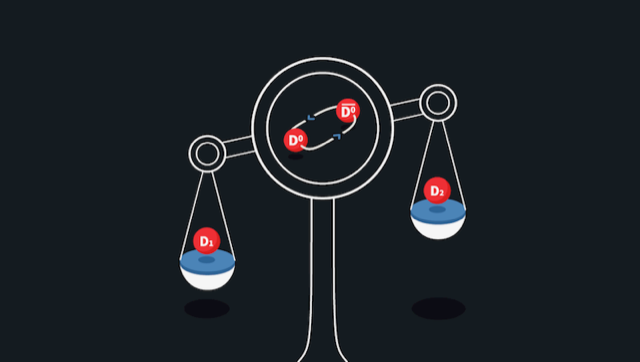
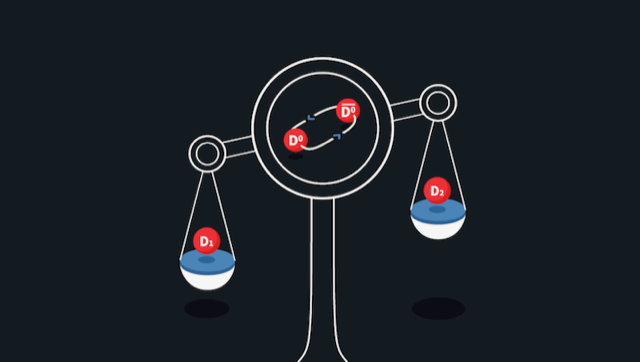
Since the construction of the first particle accelerators, increasing the energy of those accelerators has allowed physicists to produce and discover heavier and heavier particles. Those discoveries have extended our knowledge of the subatomic world and eventually resulted in the theoretical framework called the standard model. New particles may be directly produced in high-energy particle collisions. But an alternative particle search strategy involves studying a quantum-mechanical process in which a particle turns into its own antiparticle and back again. This phenomenon, known as mixing, can occur with neutral mesons (bound states of a quark and an antiquark) and was first observed with mesons in the 1950s. Mixing is interesting for particle searches because it is affected by—and thus may reveal—other particles to which the mixing mesons couple during the oscillation. Some of these particles may be so heavy that they could not be directly produced by even the most powerful particle colliders. The Large Hadron Collider beauty (LHCb) Collaboration has now characterized mixing for the -meson system, measuring a key mixing parameter—related to the mass difference between two of the meson “eigenstates” involved in the mixing (Fig. 1)—that is sensitive to the presence of those heavy particles [1]. The result provided no hints of new particles and allowed the collaboration to determine a minuscule mass difference of about g.
Mesons are short-lived. However, four neutral mesons—the (composed of a quark and an antiquark), and —live long enough so that they can change into their own antiparticle before they decay. At a given time, each of the observable mesons exists as a linear combination of a pure particle state or and of a pure antiparticle state . As for any quantum system in a two-state superposition, the Schrödinger equation predicts an oscillatory time evolution of . Much like neutrino oscillations, meson oscillations occur because and aren’t the mass eigenstates of the system’s Hamiltonian. The eigenstates are instead symmetric and antisymmetric combinations of the and , with each eigenstate having different mass and lifetime. In this formalism, the mixing rate is governed by two parameters. The first, , is proportional to the mass difference between the two eigenstates while the second, , is proportional to the lifetime difference.
Meson mixing occurs through intermediate states reached through the decays of and . For example, both and can decay to a pair of mesons (Fig. 2, left). Other intermediate states involve virtual particles such as bosons (Fig. 2, right), which have masses much larger than the meson. Such heavy intermediate states can affect the value of , which means that a measurement of this parameter can potentially reveal the presence of heavy particles that the collider cannot produce. Indeed, the 1987 discovery of mixing [2] revealed an value, implying that one of the involved intermediate states involved a heavy particle—the top quark, whose existence was only confirmed eight years later [3].
is the only one of the four mesons for which has not yet been measured. It is also the only one of these mesons that consists of up-type quarks ( ), while the others consist of down-type quarks ( ). mixing is thus especially interesting, as it could be sensitive to different particles than the mixing of the other three mesons—including particles not considered by the standard model.
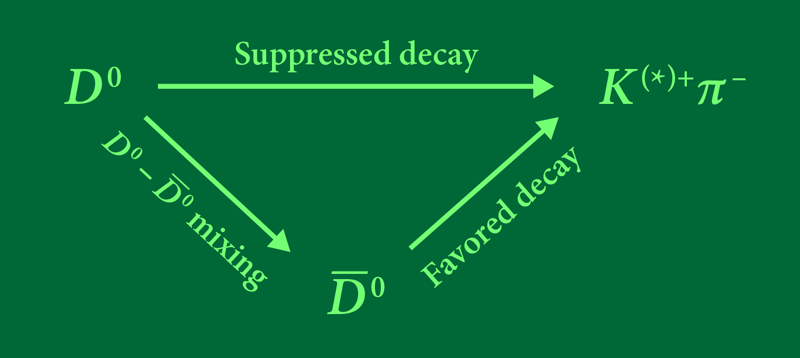
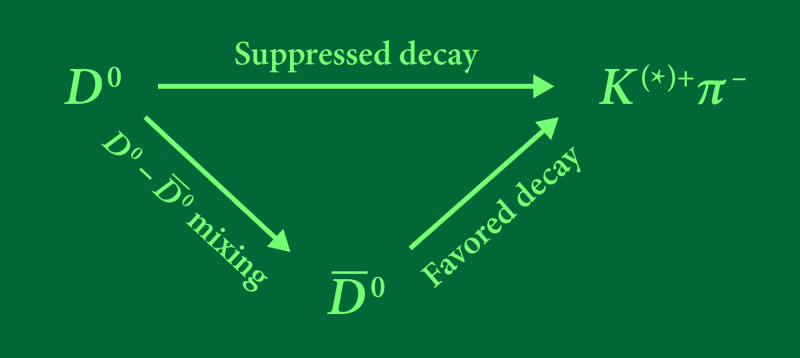
Neutral mesons are copiously produced in the proton-proton collisions of CERN’s Large Hadron Collider. LHCb discovered mixing in 2013 (see Viewpoint: Observing Matter-Antimatter Oscillations) [4] using a technique that involved characterizing the decays of the meson ( or ) at 13 different delays after production. To find evidence for the oscillation, they compared the rates of two decays. The first decay is a so-called “right-sign” (RS) decay , which proceeds at high rate because it is favored by the weak interaction. The second, “wrong-sign” (WS) decay proceeds either directly through the unfavored decay of to or indirectly through an oscillation from into a , which then decays through its favored decay to the same final state (Fig. 3). The WS decay is “suppressed” compared to the RS decay. The observation of a component in the WS-RS ratio that increased linearly in time signaled the production of due to meson mixing. From the 2013 experiment, the LHCb Collaboration could only determine , as the WS-RS signal they observed didn’t depend on .
In the new experiment, LHCb has measured mixing using the decay to a different final state—the three-particle final state [1], where is a neutral, short-lived kaon. Several intermediate states, some of which involve the vector meson, contribute to this decay. For example, contributions are provided by the WS decay (through either the mixing path or through a direct decay similar to the decay ) followed by . The corresponding RS decay would be followed by . In the experiment, the RS decays and the WS decays are accumulated in a different region of the three-particle “phase space”—a space that offers a convenient statistical representation of a large ensemble of particles based on their position and momenta. The LHCb Collaboration measures WS-RS ratios in eight distinct regions of the phase space. As theory indicates, the ratio in each region is sensitive to a different combination of and . By analyzing the WS-RS ratio as a function of decay time in the eight regions, the researchers could thus determine both and .
The LHCb Collaboration measured to be 7 standard deviations away from zero and determined, with the same statistical significance, the mass difference between the two meson eigenstates to be . The value falls within the range predicted by the standard model [5] and thus does not provide evidence for new, massive particles. This measurement, however, will allow theorists to constrain the properties of potential new particles. What’s more, this measurement of will help ongoing searches for charge-parity (CP) symmetry violations in the -meson system—subtle differences between the decays of and of to the same final state or between the matter-to-antimatter oscillation ( to ) and the antimatter-matter oscillation ( to ). Slight differences between the behavior of the and that of may hold the key for solving one of the greatest mysteries in science—why matter dominates over antimatter in the Universe.
mixing remains a promising path for finding evidence of yet undiscovered particles, and it will continue to be scrutinized by a substantial research program to be carried out both by the LHCb experiment and by the Belle II experiment in Japan.
References
- R. Aaij et al. (LHCb Collaboration), “Observation of the mass difference between neutral charm-meson eigenstates,” Phys. Rev. Lett. 127, 111801 (2021).
- H. Albrecht et al. (ARGUS Collaboration), “Observation of mixing,” Phys. Lett. B 192, 245 (1987).
- F. Abe et al. (CDF Collaboration), “Observation of top quark production in collisions with the collider detector at Fermilab,” Phys. Rev. Lett. 74, 2626 (1995); S. Abachi et al. (D0 Collaboration), “Observation of the top quark,” Phys. Rev. Lett 74, 2632 (1995).
- R. Aaij et al. (LHCb Collaboration), “Observation of oscillations,” Phys. Rev. Lett. 110, 101802 (2013).
- I. I. Bigi and N. G. Uraltsev, “ oscillations as a probe of quark–hadron duality,” Nucl. Phys. B 592, 92 (2001); A. F. Falk et al., “The mass difference from a dispersion relation,” Phys. Rev. D 69, 114021 (2004).