PRX—Ten Years After

F. Krzakala et al., Phys. Rev. X (2012)

F. Krzakala et al., Phys. Rev. X (2012)

×

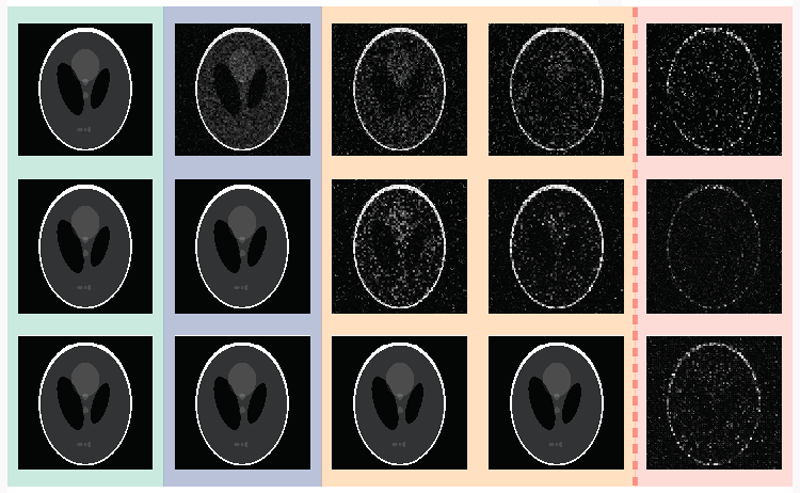
Sharply knock a bottle of supercooled water, and it spontaneously freezes into slushy ice. This exciting phenomenon inspired Florent Krzakala, now at the Swiss Federal Institute of Technology in Lausanne, Switzerland, and colleagues to construct an algorithm for recovering images from sparse signals via compressed sensing. As described in a 2012 paper, the method resembles supercooled water freezing, in that the reconstruction grows rapidly from a tiny initial image fragment.

Compressed sensing is used to reconstruct an image from a few randomly selected measurements. The U.S. Food and Drug Administration approved the method for use in magnetic resonance imaging, significantly reducing the time that patients have to sit in scanners. Krzakala and colleagues showed that they could improve on previous compressed sensing algorithms to further reduce the number of data points—and the number of computations—required to get an image.

–David Donoho, Stanford University

F. Krzakala et al., “Statistical-physics-based reconstruction in compressed sensing,” Phys. Rev. X 2, 021005 (2012).

H. Weng et al., Phys. Rev. X (2015)

H. Weng et al., Phys. Rev. X (2015)

×

In 2015, researchers discovered analogs of Weyl fermions—massless, chiral particles predicted by quantum field theory—in solids whose electronic bands cross at “Weyl nodes” near the Fermi surface. PRX published one of the discovery papers, by Hong Ding of the Chinese Academy of Sciences (CAS) and colleagues, who found Weyl fermions in tantalum arsenide (TaAs).

A study by Hongming Weng and colleagues at CAS helped in laying the foundations for the discovery. Their theoretical calculations had suggested that a family of nonmagnetic materials including TaAs was a promising target for spotting the quasiparticles. After the discovery, a paper by Genfu Chen, also at CAS, and colleagues reported measurements of the “chiral-anomaly” property of Weyl fermions, confirming a predicted imbalance of the handedness, or chirality, of these quasiparticles when the material is subjected to certain electric and magnetic fields.

The discovery of Weyl semimetals has spurred tremendous interest in topological semimetals and led to the discovery of many other exotic materials. The research field remains vibrant, with extensive efforts to harness the materials’ properties in devices.

–Shuyun Zhou, Tsinghua University, China

H. Weng et al., “Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides,” Phys. Rev. X 5, 011029.

B.  Q. Lv et al., “Experimental discovery of Weyl semimetal TaAs,” Phys. Rev. X 5, 031013 (2015).

See also Viewpoint: Where the Weyl Things Are.

X. Huang et al., “Observation of the chiral-anomaly-induced negative magnetoresistance in 3D Weyl semimetal TaAs,” Phys. Rev. X 5, 031023 (2015).

Thermodynamic laws are usually derived for large (classical) systems, so the corresponding limitations for small (quantum) machines are still not completely understood. Building on previous work that looked at a quantum origin of the second law of thermodynamics, Matteo Lostaglio and colleagues from Imperial College London applied a resource theory approach to the description of quantum states. In resource theories, one takes an agent-based view of quantum machines, imagining that the agent switches interactions with the environment on and off. From this perspective, one asks, which transformations among possible quantum states are possible?

Lostaglio and colleagues found that state transformations are limited not only by the second law but also by other thermodynamic constraints. As the paper showed, symmetries are key to figuring out what can happen in the quantum realm. And the answers were fascinating: While quantum theory poses additional constraints, quantum machines have access to quantum coherences that can open up transformations not accessible to classical machines. Whether these coherences lead to new capabilities is a matter of ongoing research.

–Marcus Huber, Institute of Quantum Optics and Quantum Information, Austria

M. Lostaglio et al., “Quantum coherence, time-translation symmetry, and thermodynamics,” Phys. Rev. X 5, 021001 (2015).

See also Viewpoint: New Entry in the Thermodynamic Rulebook for Quantum Systems.

F. Ginot et al., Phys. Rev. X (2015)

F. Ginot et al., Phys. Rev. X (2015)

×

Active systems are composed of self-driven objects, such as bacteria or colloidal particles, that convert stored or ambient energy into motion. Active systems are intrinsically out of equilibrium and are thus difficult to describe with an equation of state that relates statistical mechanics properties like density and temperature.

In a 2015 paper, Cécile Cottin-Bizonne of the Univeristy of Lyon, France, and her co-workers reported the first combined experimental and theoretical study aimed at finding the nonequilibrium equation of state for active systems. The team investigated a 2D assembly of self-propelled micrometer-wide spheres and compared their results with numerical simulations of self-propelled hard disks.

At low densities, the team found an “effective” temperature to describe the state of the self-propelled particles, with the equation of state matching that of an ideal gas. At higher densities, they recovered a state equation reminiscent of that describing colloidal systems with attractive interactions. The work paved the way for other studies of the statistical mechanics of active systems.

–Chantal Valeriani, Complutense University of Madrid, Spain

F. Ginot et al., “Nonequilibrium equation of state in suspensions of active colloids,” Phys. Rev. X 5, 011004 (2015).

Many-body localization (MBL) occurs when strong disorder prevents a system from reaching thermal equilibrium, and local memory of initial conditions persists forever. The system can thermalize only after going through a phase transition, provoked by changes in some parameter, such as the strength of disorder. This transition is visible in the dynamical evolution of the system but not in the thermodynamics, and it cannot be understood within traditional approaches to the study of phase transitions. In 2015, a set of pioneering papers—the first by Sid Parameswaran from the University of Oxford, UK, and colleagues; the second by Ehud Altman from the University of California, Berkeley, and collaborators—described the MBL phase transition within a renormalization group treatment. Such a treatment provides a coarse-grained picture of the transition as a competition between two types of regions—thermal and localized—on different length scales.

These works opened the door to many important developments, including an avalanche-based description of the growth of thermal regions in localized backgrounds, with important implications for the stability of MBL. Recent work has also found a connection between the MBL phase transition and the Kosterlitz-Thouless topological phase transition.

–Vedika Khemani, Stanford University

R. Vosk et al., “Theory of the many-body localization transition in one-dimensional systems,” Phys. Rev. X 5, 031032 (2015).

A. C. Potter et al., “Universal properties of many-body delocalization transitions,” Phys. Rev. X 5, 031033 (2015).

D. Bi et al., Phys. Rev. X (2016)

D. Bi et al., Phys. Rev. X (2016)

×

Collective cell migration occurs in dense tissues during embryonic development, wound healing, and cancer metastasis. During this migration, cells change state, moving from an ordered, layered state to a disordered one. Researchers thought that this order-to-disorder transition might resemble the solid-to-liquid jamming transition that happens in colloidal glasses, but the idea remained unproven.

To investigate this cellular transition, Lisa Manning of Syracuse University, New York, and her colleagues presented in their 2016 paper a minimal numerical model that accounts for cell shape and cell motion and correctly reproduces multibody cell-cell interactions. Using the model, the group showed that a jamming-like transition could be obtained by tuning the motile speed of individual cells and the persistence time of their tracks. The paper opened the possibility of studying tissue dynamics using minimal models.

–Chantal Valeriani, Complutense University of Madrid, Spain

D. Bi et al., “Motility-driven glass and jamming transitions in biological tissues,” Phys. Rev. X 6, 021011 (2016).

P. J. J. O’Malley et al., Phys. Rev. X (2016)

P. J. J. O’Malley et al., Phys. Rev. X (2016)

×

Performing quantum chemistry calculations with molecules is a prime goal of quantum computers. In a 2016 paper, my colleagues and I reported a major step toward that goal, employing then state-of-the-art superconducting quantum computer technology to calculate the dissociation energy curves of the hydrogen molecule using just two qubits.

Calculating hydrogen was a kind of “hello world” program—the first thing someone might try with a new computer capability. But this demonstration was the first scalable implementation of chemistry simulations on a quantum computer, meaning that the method should work equally well for molecules larger and more complex than hydrogen. The paper also showcased a new quantum algorithm, termed the variational quantum eigensolver, which runs partly on a quantum computer and partly on a classical one. Since then, several other groups have employed the method to simulate larger chemical systems.

–Alán Aspuru-Guzik, University of Toronto, Canada

P. J. J. O’Malley et al., “Scalable quantum simulation of molecular energies,” Phys. Rev. X 6, 031007 (2016)

Topological phases are a preponderant theme in modern condensed-matter physics because they are robust against environmental perturbations. Researchers originally explored these phases within energy-conserving—or so-called Hermitian—quantum-mechanical systems, but the focus has lately shifted towards the non-Hermitian context, which can be explored in metamaterials and in cold-atom systems.

The relaxation of the Hermiticity constraint leads to far richer phenomena and topological classifications, as thoroughly investigated by Masahito Ueda from the University of Tokyo and colleagues in 2018 and by Masatoshi Sato from Kyoto University and colleagues in 2019. These papers showed that the number of symmetry classes increases from 10 in Hermitian systems to 38 in non-Hermitian ones. Moreover, the non-Hermitian energy landscape offers a unique spectral topology that encompasses symmetry-protected lines and point gaps.

These initial developments in non-Hermitian topology have inspired a wide range of scientific efforts. On the theory side, researchers are applying mathematical tools like algebraic geometry and complex analysis to the enriched symmetry classes, while experimentalists search for novel non-Hermitian signatures and concrete applications in lasers, sensors, electronics, and even chemical and biological networks.

–Ching Hua Lee, National University of Singapore

Z. Gong et al.,“Topological phases of non-Hermitian systems,” Phys. Rev. X 8, 031079 (2018).

K. Kawabata et al., “Symmetry and topology in non-Hermitian physics,” Phys. Rev. X 9, 041015 (2019).

See also Viewpoint: Non-Hermitian Topological Systems.

Half a century ago, researchers predicted supersolidity, an intriguing phase of matter that combines the frictionless flow of a superfluid and the crystalline structure of a solid. The prediction sparked an intense experimental quest to find a supersolid. In 2017, supersolidity was finally observed in Bose-Einstein condensates (BECs) of atomic gas coupled to light.

In 2019, three papers reported that supersolidity could be produced without employing light, by simply harnessing the intrinsic dipolar moment of the atoms. Two of these papers were published in PRX—one by Francesca Ferlaino of the University of Innsbruck, Austria, and colleagues, and the other by Tilman Pfau of the University of Stuttgart, Germany, and colleagues. BECs are superfluids. In dipolar BECs, attractive short-range interactions and long-range dipolar forces between the atoms can cause them to spontaneously clump into superfluid droplets. In turn, dipolar interactions among the droplets can cause BECs to form crystalline structures, which allowed the researchers to turn the condensates into supersolids.

These dipolar supersolids offer more flexible and controlled experimental platforms for studying supersolidity than previous ones, allowing for systematic studies of the counterintuitive properties of these exotic states of matter.

–Leticia Tarruell, The Institute of Photonic Sciences, Spain

L. Chomaz et al., “Long-lived and transient supersolid behaviors in dipolar quantum gases,” Phys. Rev. X 9, 021012 (2019)

F. Böttcher et al., “Transient supersolid properties in an array of dipolar quantum droplets,” Phys. Rev. X 9, 011051 (2019).

See also Viewpoint: Dipolar Quantum Gases Go Supersolid.