Pushing the Limits of Quantum Sensing with Variational Quantum Circuits
Since it was first introduced in 1949, Ramsey interferometry has had an exciting history. The method was at the center of a series of beautiful experiments performed by Serge Haroche’s group that were recognized by the 2012 Nobel Prize in Physics [1, 2]. The prize was given for “methods that enable the measurement and manipulation of individual quantum systems.” Haroche’s group used individual atoms to sense the properties of photons inside an optical cavity. Building on these ideas, researchers have reported a new theoretical study that points at a promising way to push the limits of quantum sensing. Raphael Kaubruegger at the University of Innsbruck, Austria, and his colleagues employ so-called variational quantum circuits to optimize the sensitivity of an atomic sensor based on entangled atoms [4]. The result is a sensor that, with surprisingly modest quantum resources, should outperform those based on standard Ramsey interferometry.
We often think of photons as probes to study atoms, but Ramsey interferometry flips the script and uses atoms to study photons. This type of interferometry first puts an atom in a superposition of electronic energy levels and then passes the atom through an optical cavity. As a result, the quantum superposition accumulates a measurable phase shift that depends on the properties of the photons in the cavity. The experiments by Haroche’s group involved passing atoms through an optical cavity one at a time in order to nondestructively detect the number of photons. More photons in the cavity lead to a larger phase shift in the atomic wave function. In such experiments, each atom can be regarded as an individual entity. In other words, each atom is prepared in an uncorrelated “product state”—a state that can be described independently of every other atom’s state.
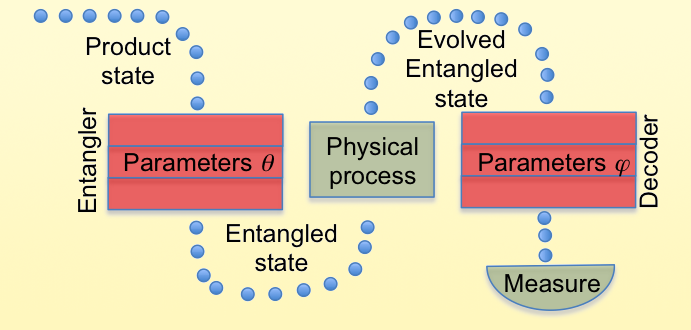
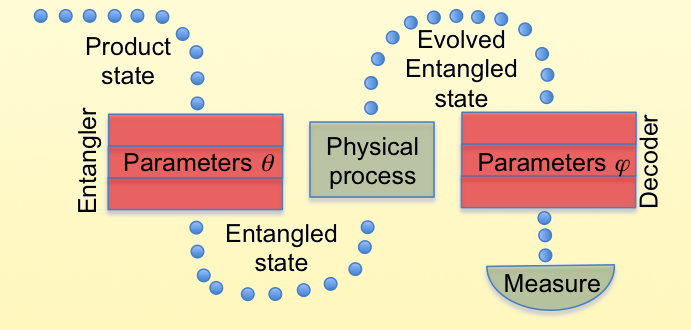
Kaubruegger and colleagues propose to go a step further by entangling 64 atoms and using them to make an even better sensor for Ramsey interferometry. They demonstrate the effectiveness of their approach by considering an optical atomic clock, in which Ramsey-interferometry measurements of the atomic ensemble’s phase are used to correct the clock’s laser frequency (Fig. 1). Like Haroche’s group, the researchers manipulate a single quantum system, but one made of 64 atoms. Rather than using atoms in the product state, they propose to prepare these atoms in an entangled state, in which each atom’s state cannot be fully described independently of the other atoms. They show that performing Ramsey interferometry using entangled states gives a big boost to the sensitivity of the phase sensor, beating the standard quantum limit that applies when sensing using uncorrelated atoms.
Their proposal harnesses a key innovation to prepare the entangled state. Entangled atomic sensors have been employed before, and a standard approach involves using so-called Greenberger-Horne-Zeilinger (GHZ) states. Kaubruegger and colleagues note that these states are only optimal for sensing under certain assumptions regarding prior knowledge of the phase-shift value. This limitation opened the door for the researchers to improve upon and outperform GHZ states by taking advantage of one of today’s hottest concepts in quantum computing: variational quantum circuits. These circuits, which have a set of free parameters, replace the fixed quantum circuits used to implement quantum algorithms such as Shor’s algorithm for factoring or the Harrow-Hassidim-Lloyd algorithm for solving linear systems. Variational quantum circuits have internal parameters (such as rotation angles about certain Bloch sphere axes) that one optimizes over to perform a given task. Kaubruegger and colleagues propose to use two sets of variational quantum circuits to prepare the entangled state for sensing and to measure the parameter that they want to sense (that is, the optical phase). They call these circuits the entangling and decoding circuits, respectively (Fig. 2).
Achieving good performance with variational quantum circuits is challenging, since the parameters can be hard to optimize and one does not know ahead of time how deep of a circuit one needs, that is, how many quantum gates are required. Kaubruegger and colleagues find that excellent performance can be achieved with “shallow” circuits composed using the quantum resources inherently available in Ramsey interferometry and atomic-clock platforms. With only a few layers of their quantum circuits, they not only beat the standard quantum limit (which applies to measurements made using uncorrelated atoms) but also get very close to the Heisenberg limit—the ultimate limit for the sensitivity that one can achieve with a quantum system and, therefore, the ultimate limit of a quantum sensor. Here, a layer refers to the building block of the variational quantum circuit: more layers are needed to do a more comprehensive search over the Hilbert space, whereas fewer layers can only search over a smaller subspace. The fact that good performance requires only a few layers suggests that states that are beneficial to quantum metrology are relatively easy to find. This is an exciting possibility that should stimulate more investigation.
This new work is important because it brings together two different communities: the quantum sensing community and the variational quantum algorithm community. While variational quantum algorithms are getting major attention for quantum computing applications, it is rare for them to appear in an atomic experimental setting or in a sensing setting. The beautiful observation that variational algorithms could work in a realistic sensing application should inspire many experimentalists to think about optimizing their setups with variational quantum circuits, regardless of whether they involve atoms, light, spins, or superconductors. We need cross fertilization between quantum experimentalists and quantum computer scientists, and this work gives an inspiring guide for how such cross fertilization can be brought about.
References
- C. Guerlin et al., “Progressive field-state collapse and quantum non-demolition photon counting,” Nature 448, 889 (2007).
- S. Deléglise et al., “Reconstruction of non-classical cavity field states with snapshots of their decoherence,” Nature 455, 510 (2008).
- S. Gleyzes et al., “Quantum jumps of light recording the birth and death of a photon in a cavity,” Nature 446, 297 (2007).
- R. Kaubruegger et al., “Quantum variational optimization of Ramsey interferometry and atomic clocks,” Phys. Rev. X 11, 041045 (2021).