Speeding Up Ultrafast Spectroscopy
Ultrafast spectroscopy would be an ideal characterization technique for many scientific and industrial applications if only it weren’t so slow. To accurately characterize a given sample, thousands of time-consuming individual measurements must usually be made, adding up to a process that can take minutes or even hours. But what if we could forgo most of these measurements without compromising the technique’s reliability? This solution may seem too good to be true, but it is one that has now been demonstrated by Sushovit Adhikari at the Argonne National Laboratory, Illinois, and colleagues. The team applied an algorithmic approach called compressive sensing (CS) to two ultrafast spectroscopy techniques, reducing their measurement time by a factor of 6 [1]. This improvement may make a new range of condensed-matter experiments more broadly accessible. It could also bring cutting-edge optical technologies closer to industrial applications, especially in the field of product quality control.
Spectroscopic characterization techniques possess an intrinsic trade-off between data-acquisition speed and measurement sensitivity. Repeating measurements reduces experimental noise and increases accuracy through an averaging process, but more time is then required to collect a full dataset. There are two complementary approaches to address this challenge: a “hardware” approach, which focuses on improving the experimental equipment by, for example, increasing detector sensitivity, boosting signal emission, or reducing environmental noise; and a “software” approach, in which data acquisition is accelerated by means of signal-processing tools. As a mathematical algorithm for fitting and reconstructing experimental data, CS falls into this latter category. Developed in the 1990s and 2000s [2–4], the approach is often associated with the fields of nuclear magnetic resonance (NMR) and spatial imaging, where it was first deployed [4–7]. But the concept can be applied to virtually any experimental signal.
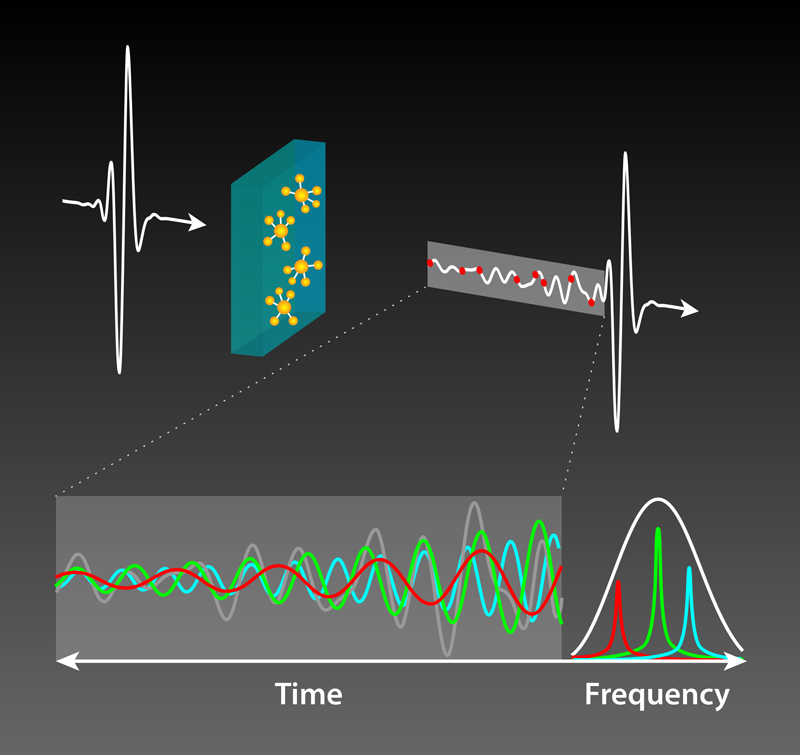
CS involves reconstructing a signal from a randomly (and drastically) downsampled dataset. In comparison to standard methods of data collection, therefore, CS saves lab time by allowing experimentalists to rely on fewer sampled data points while achieving the same resolution. It is not quite a free lunch though—the measured signal must obey an important condition: that it is sparse when transformed into another known basis. For instance, a signal that at first appears complex might, when transformed into another basis, turn out to be dominated by just a small number of select frequencies (Fig. 1). Such a signal is sparse in the frequency domain and can be efficiently analyzed with CS. This condition may seem restrictive, but it is fulfilled by many signals.
As Adhikari and colleagues show, the ability of CS to make do with fewer data points makes the technique particularly well suited to multidimensional measurements. Obtaining such measurements using a conventional signal-processing method would usually involve scanning over the full parameter space in every variable. By downsampling this parameter space for each variable, CS allows these measurements to be made with significant data-acquisition-rate benefits [1, 4–8]. This efficiency improvement has the added advantage that samples are less prone to degradation from long exposure to the probe. In the case of characterization techniques that use beams of electrons or ionizing photons, some materials cannot withstand the high dose associated with a long averaging time [6]. CS thereby helps to overcome limitations related to both sample throughput and measurement stability.
Adhikari and colleagues demonstrate this advantage by using CS to reduce, by a factor of 6, the data acquisition for two optical pump-probe experiments: ultrafast transient absorption spectroscopy and ultrafast terahertz (THz) spectroscopy [1]. In both experiments, data acquisition takes place over two dimensions. In other words, data are collected while varying two independent experimental parameters such as the time interval between optical pulses and the optical wavelength. The team’s first step is to randomly downsample this measurement space. They do this at different sampling fractions to verify the integrity of the reconstruction for various amounts of data. They also present a strategy to validate the reconstruction process as more data are added. This validation would be achieved by repeating the CS reconstruction for each new data point until the error between consecutive reconstructions falls below a certain threshold.
Experimentalists looking to replicate the team’s approach with other characterization techniques will be glad to know that they do not have to start from scratch. Code packages and demonstrations are notably available for Matlab [5] and Python [9], with the small caveat that they will need to be adapted to each type of measurement by integrating the numerical tools into the instrumental automation aspect, selecting a correct sparse basis transformation, and defining appropriate stopping criteria.
After the success of CS in applications such as NMR [5], single-pixel imaging [4], and quantum chemistry [8], we expect this new demonstration to raise the technique’s profile within the broad ultrafast-spectroscopy community. Longer term, machine learning and CS could be combined synergistically [7] to automate the process of deducing the ideal transformation that delivers the necessary sparse bases for the CS algorithm.
Despite the potential of CS to improve the efficiency of ultrafast spectroscopy, researchers should bear in mind a significant limitation: CS may not perform well if the signal is not actually sparse. Nevertheless, we imagine that this technique could be a natural match to spectroscopy applications that seek to investigate and quantify spectral resonances in materials. We expect that “software-like” advances will gain ground, especially in industry, where they may be crucial to the implementation of ultrafast techniques for product characterization.
References
- S. Adhikari et al., “Accelerating ultrafast spectroscopy with compressive sensing,” Phys. Rev. Applied 15, 024032 (2021).
- D. L. Donoho, “Compressed sensing,” IEEE Trans. Inf. Theory 52, 1289 (2006).
- E. J. Candes and M. B. Wakin, “An introduction to compressive sampling,” IEEE Signal Process. Mag. 25, 21 (2008).
- G. M. Gibson et al., “Single-pixel imaging 12 years on: A review,” Opt. Express 28, 28190 (2020).
- A. Shchukina et al., “Pitfalls in compressed sensing reconstruction and how to avoid them,” J Biomol. NMR 68, 79 (2016).
- L. Kovarik et al., “Implementing an accurate and rapid sparse sampling approach for low-dose atomic resolution STEM imaging,” Appl. Phys. Lett. 109, 164102 (2016).
- A. Bustin et al., “From compressed-sensing to artificial intelligence-based cardiac MRI reconstruction,” Front. Cardiovasc. Med. 7, 17 (2020).
- J. N. Sanders et al., “Compressed sensing for multidimensional spectroscopy experiments,” J. Phys. Chem. Lett. 3, 2697 (2012).
- M. Kliesch, “pit—Pictures: Iterative Thresholding algorithms,” GitHub repository, https://github.com/MartKl/CS_image_recovery_demo (2020).