Boosting Inertial-Confinement-Fusion Yield with Magnetized Fuel

John D. Moody

Trend

Boosting Inertial-Confinement-Fusion Yield with Magnetized Fuel

Lawrence Livermore National Laboratory, Livermore, CA, USA

May 5, 2021• Physics 14, 51

Building on a decade of advances in the understanding of neutron production and hot-spot physics, researchers at the National Ignition Facility are pursuing magnetized fusion fuel as a potentially disruptive way to boost the performance of laser-driven implosion.

ARTICLE TAKEAWAYS

A new project at the National Ignition Facility is seeking to use magnetized fusion fuel to boost high-performing implosions into the high-fusion-energy-gain regime.

Magnetized fusion fuel reduces heat loss from the plasma by constraining the motion of electrons and alpha particles, improving the chances of achieving runaway self-heating in a laboratory plasma for the first time.

Significant scientific and technological challenges must be overcome for this project to succeed.

Creating and maintaining self-sustaining nuclear fusion reactions in the laboratory, such that energy output exceeds energy input, continues to challenge physicists worldwide. While some experiments have demonstrated significant energy release from fusion reactions, none have yet reached the ignition and high-fusion-energy-gain regime—the point at which “runaway” self-heating occurs. The problem is one of confinement: fusing enough nuclei for the reaction to become self-sustaining means bottling up a superheated plasma that wants desperately to expand and cool.

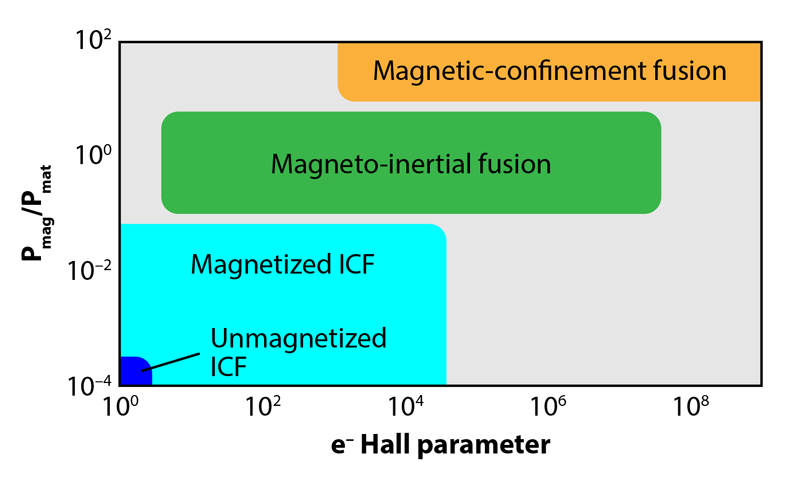
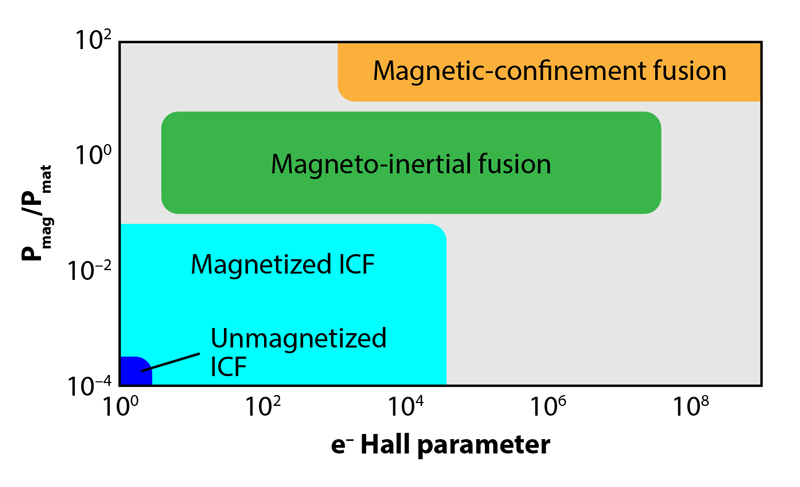
In the most widely used approach to tackling this problem, scientists seek to apply the necessary confining pressure via powerful magnetic fields. In these magnetic confinement fusion (MCF) schemes, the plasma circulates in a steady state within a torus-shaped chamber. Although at an extremely high temperature ( $\sim 5$ keV, or 60 million kelvin), an MCF plasma has a low density $(< 1 0^{- 9} {g/cm}^{3})$ , and the energy that it carries is much smaller than that of the magnetic field. The magnetic field therefore dominates the plasma’s motion, slowing its escape and strongly reducing heat loss.

In other fusion experiments, the magnetic field plays a smaller role. The various approaches can be characterized according to the strength of particle magnetization and the importance of the magnetic field on the plasma dynamics. MCF schemes occupy the upper extreme of both scales, while at the other end lies a technique that involves no externally applied magnetic field at all (Fig. 1). This approach, called inertial confinement fusion (ICF), triggers fusion using an impulsive driver (such as high-powered lasers, ion beams, or pulsed electrical power) to rapidly compress and heat around half a milligram of deuterium-tritium (DT) fuel.

At the National Ignition Facility (NIF) at Lawrence Livermore National Laboratory (LLNL) in California, we are using a laser-driven version of ICF known as the indirect-drive method [1]. Here, laser beams target a small metal cylinder called a hohlraum, enclosed within which is a spherical capsule containing frozen DT fuel. The laser energy excites the hohlraum material (usually gold), generating x-ray radiation in all directions. The x rays implode the fuel capsule at high velocity, via ablation, until the fuel stagnates at the center of the capsule. This implosion generates a “hot spot” within which the plasma reaches a temperature similar to that achieved in MCF but a far greater density $(100 {g/cm}^{3})$ . If the plasma is sufficiently hot and dense, this process can ignite fusion in the form of a thermonuclear burn wave that propagates outward into the compressed DT fuel. The reaction is powered by the energy deposition of the alpha-particle (helium-4) output products, and it can result in high fusion-energy gains—defined as the ratio of the fusion-energy yield to the input laser drive energy.

The complete burn of 0.5 mg of 50:50 DT fuel mixture (with each reaction yielding a neutron, an alpha particle, and an excess energy of 17.6 MeV) would release energy sufficient to power an average home for a few days. But a typical experiment at NIF releases only 0.1% of the full amount. The reason for this discrepancy is that plasma heating from the fusion alphas doesn’t yet substantially exceed the heat loss from radiation and electron thermal conduction. Consequently, the temperature of the plasma falls and fusion reactions slow and then stop.

To mitigate this heat loss, we are planning to implement a modified version of ICF, called magnetized ICF, which adds a magnetic field to the fuel capsule. In this new approach, the magnetic field is not large enough to have much of an effect on the hot-spot plasma dynamics, but it should increase the energy returned from the process by insulating thermal losses and increasing alpha-particle heating.

Figure caption — **Figure 1:** Three approaches to laboratory fusion are shown according to the strength of the magnetic field ( $e^{-}$ Hall parameter, or the electron cyclotron frequency times the electron-ion collision time) and the relative importance of the magnetic field on plasma dynamics (expressed as the ratio of magnetic to thermal energy density, $P_{mag} ∕ P_{mat}$ ).

Best of Both Worlds

The idea of combining inertial and magnetic confinement (magneto-inertial confinement, occupying the intermediate range in Fig. 1) dates back at least to 1962 and the work of George Linhart, who proposed using it with explosive drivers [2]. Over the next several decades, as laser, particle-beam, impact, and other drivers entered the scene, researchers proposed adding magnetic fields to fuel volumes in these systems as well. The idea is that, according to the “frozen-in law” of magnetohydrodynamics, an initial magnetic field of around 50 T is amplified enormously as the plasma—and the magnetic field—is compressed. The final field, which can reach in excess of 10 kT, reduces thermal conduction losses and enhances alpha-particle energy deposition in the plasma by constraining the motion of charged particles. By reducing such energy losses, fusion output increases and the driver requirements for achieving ignition can be relaxed.

Recent investigations into magnetized fusion fuel by the National ICF Program have shown promise. Starting in 2010, researchers at the Laboratory for Laser Energetics (LLE) at the University of Rochester, New York, successfully demonstrated magnetic compression in a cylindrical direct-drive implosion [3, 4]. This was followed in 2011 by the first magnetized laser direct-drive spherical implosion experiment [5]. In broad accordance with model predictions, they achieved a modest but observable 15% increase in ion temperature and a 30% increase in neutron yield, indicating an enhanced fusion reaction.

Several years later in 2014, magnetized fuel was tested as part of the Magneto-Inertial Magnetic Direct Drive (MI-MDD) program at the Sandia National Laboratory, Albequerque, New Mexico. This experiment employed the MagLIF (Magnetized Liner Inertial Fusion) approach, a magneto-inertial fusion scheme which uses the inward directed Lorentz force generated by an intense current through a cylindrical metal liner to rapidly compress the enclosed fuel [6]. The team compared MagLIF’s baseline performance with setups in which the deuterium fuel was both magnetized and laser preheated. With both of these additional conditions, the experiment achieved a roughly threefold increase in plasma temperature and a 200-fold increase in neutron yield [7].

In 2015, scientists at LLNL started a three-year project to lay the groundwork for magnetized indirect-drive experiments on the NIF [8]. The theoretical part of this work showed that implosions close to triggering a fusion burn can be pushed over the threshold with a 50-T seed field in the fuel. A second three-year project at LLNL has recently started with the goal of demonstrating key scientific elements of magnetized NIF implosions experimentally [9]. If magnetized fuel in a NIF implosion shows close to the anticipated performance improvement, then this technology will become available to augment any implosion design on NIF. The results will inspire future design options that combine magnetic and inertial confinement fusion physics to possibly achieve ignition and high fusion-energy gain.

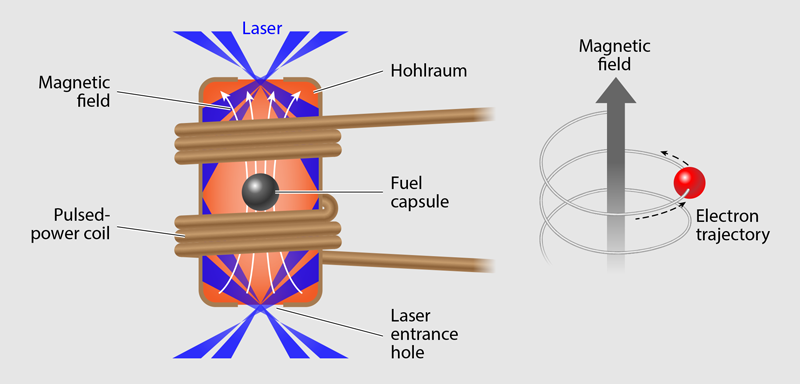
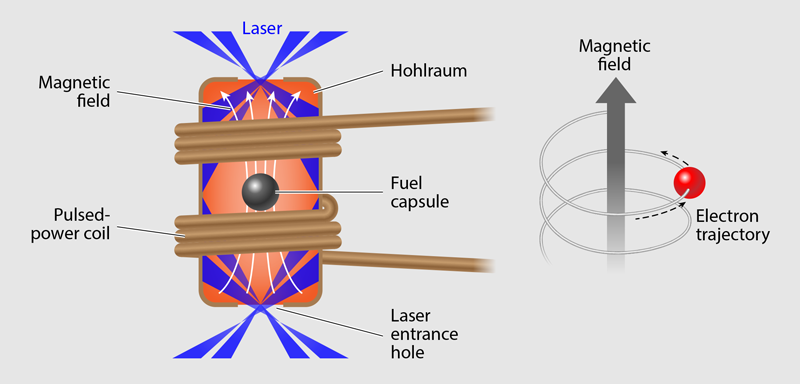
To achieve this goal requires tackling several key scientific and technological challenges that are best explained by describing how a magnetized indirect-drive implosion works. The first magnetized hohlraum target imploded at NIF (on March 1, 2021) is sketched in Fig. 2. The most visible change from a standard target is that a solenoidal coil of insulated copper wire is wrapped around the outside of the hohlraum. A pulsed-power system drives currents of tens of kiloamps through the coil in the 2 to 5 $𝜇$ s before the laser fires. This coil requires precision temperature control to allow the deposition of a smooth cryogenic fuel layer in the fuel capsule. In addition, the coil must not interfere with laser-beam access or diagnostic views of the imploding core, and it must meet stringent debris and shrapnel requirements to protect the laser optics and diagnostics from damage.

A second, less visible change from the standard target is the hohlraum material. Typical NIF hohlraum targets have a $30 - 𝜇$ m-thick wall (about the thickness of a human hair) made of gold, which efficiently converts laser light to x rays. However, gold’s low electrical resistivity means that a rapidly applied external magnetic field generates eddy currents in the wall, extending the time that it takes for the field to soak through and fill the inside of the hohlraum. The soak-through process takes about 2.5 $𝜇$ s, during which time magnetic forces start to crush the hohlraum wall, pushing it inward by more than 0.1 mm and causing it to melt. Both the deformation and melting cause the experiment to fail. Ramping the external magnetic field very slowly can mitigate the problem, but this solution requires a room full of capacitors for the required energy storage.

Instead, we invented a new hohlraum material that converts the NIF laser power to x rays with an efficiency close to that of gold but that allows the field to soak through much more quickly [10]. The design of this material was guided by the Norbury-Linde rule, which says that alloys with large valence differences have more defects and, therefore, increased electrical resistivity. We discovered that an alloy of 20% gold and 80% tantalum (atomic percent) achieves a resistivity around 200 times that of pure gold [11]. Laser conversion measurements on NIF show that this new material is at least 95% as efficient as pure gold at generating x rays, while field soak-through measurements show the expected near-instantaneous ( $\sim 20$ ns) soak-through time and no observable wall deformation.

Testing Expectations with Experiments

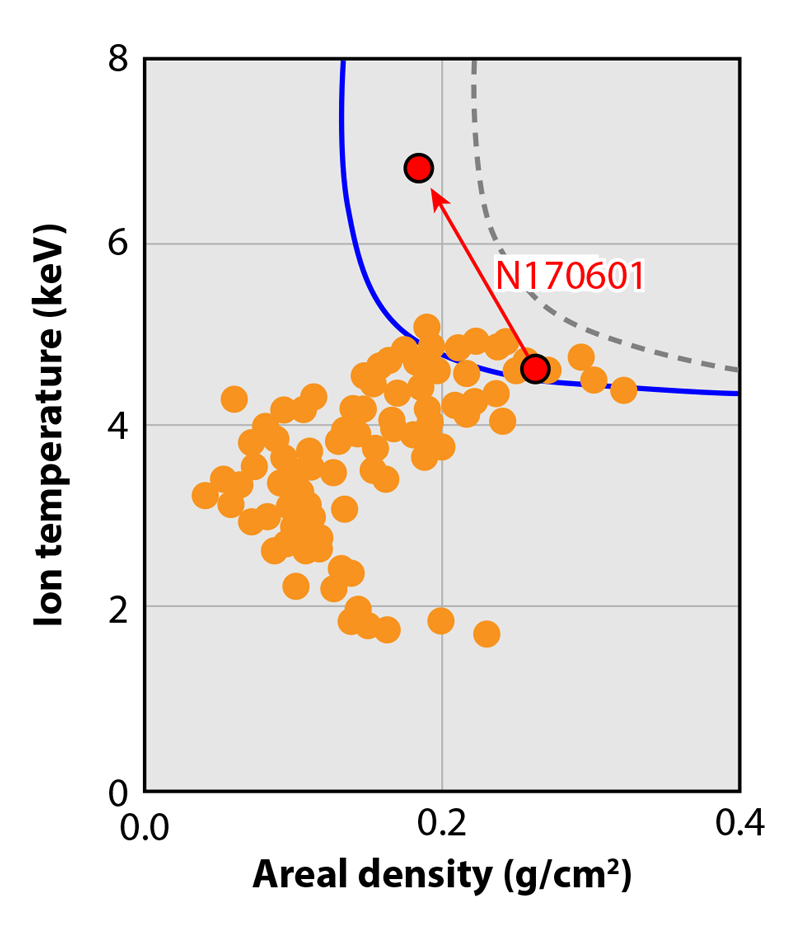
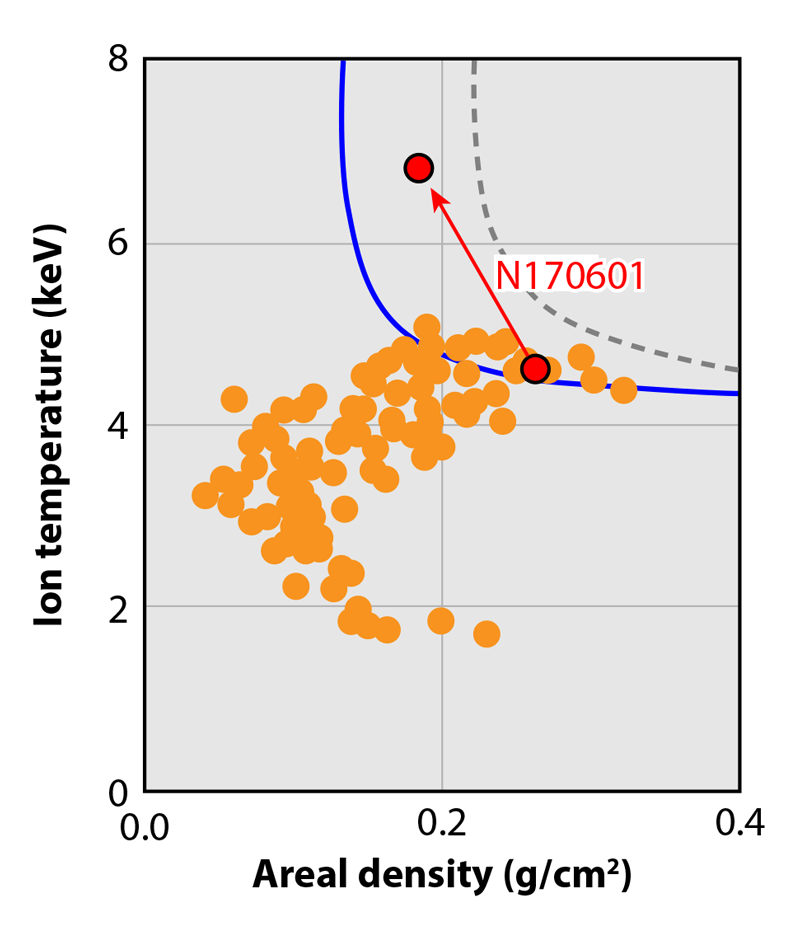
Two key parameters that describe an ICF implosion core are the temperature of the fusing particles (referred to as the ion temperature) and the areal density of the core (density $\times$ radius). The areal density value determines how much of the energy from a 3.5-MeV alpha-particle fusion product is reabsorbed by the hot spot before the alpha particle escapes. Typically, NIF implosion hot spots reach 4–5 keV and reabsorb about 70% of the alpha-particle energy. Figure 3 shows a collection of DT implosions performed on NIF over eight years, plotted according to their ion temperature and core areal-density values [12]. The dotted grey line shows the approximate boundary calculated for a self-heating hot spot where the alpha-particle heating matches the most significant losses from thermal conduction and radiation. An igniting plasma, which undergoes runaway self-heating, must be to the right of this boundary, and some NIF implosions come close.

Magnetizing the fuel helps to retain energy by effectively shutting off electron thermal conduction loss perpendicular to the direction of the field and cutting the overall thermal heat loss to about one-third of its unmagnetized value. This is the best-case estimate for a purely axial field; an azimuthal field could, in theory, eliminate heat loss altogether, but no one has devised a practical way to create such a field. In addition, the amplified field in the hot spot confines alpha particles for longer, increasing their energy deposition. The result is that the boundary for achieving a self-heating hot spot shifts to the left, as shown by the blue line in Fig. 3. This shift indicates that an igniting plasma can be achieved at a lower areal density. Based on estimates from previous experiments at NIF [12], magnetization should increase the temperature of a particular high-performing NIF implosion experiment, or “shot,” by about 2 keV while causing a slight decrease in areal density (see the red arrow in Fig. 3). This magnetized shot would be squarely in the range of a burning plasma. Detailed simulations that have already been validated by unmagnetized experiments closely reproduce these estimates of the ion temperature and areal-density values that should be achieved using magnetized fuel.

Conventional (unmagnetized) shots at NIF use targets containing frozen DT fuel. As cryogenic systems have not yet been integrated with the necessary high-current pulsed-power systems, the first tests of magnetized-implosion science on NIF are using a “warm” (room-temperature) capsule filled with deuterium and helium-4 gas. In such experiments, only the deuterium fuses, while the helium serves to “dud” the reaction. The resulting low-yield implosions are less demanding logistically but should still show the effects of magnetization: A seed field of 30 T is predicted to give an easily measurable ion-temperature increase of 0.5–1 keV and a neutron-yield increase of 50%. Alpha-particle heating is too small to matter for this gas-filled capsule implosion.

Comparing these experiments to simulations will show if magnetization is fully effective or if it is mitigated by mechanisms that cause some of the field to leave the core. To understand the process will require thinking about the data in new ways. For example, in an unmagnetized spherical implosion, measuring the neutron energy spectrum along a single viewing direction indicates the overall areal density. However, with magnetized fuel, we expect differences in the neutron energy spectra along and across the magnetic field, even for a spherical implosion, and these differences may give evidence of the compressed field amplitude in the hot spot [13].

The cryogenic DT-layered implosion design that we will eventually use to test magnetization was selected on the basis of its demonstrated reproducibility and robustness in unmagnetized NIF experiments [14]. If magnetization proves effective, we will develop new implosion designs that fully leverage the magnetic-field-induced enhancement. This could entail adding a magnetic field to several of the best-performing NIF platforms or something quite different. We expect a magnetic field to allow us to push a range of implosion designs closer to, or into, the ignition and high-fusion-energy-gain regime.

References

J. D. Lindl et al., “The physics basis for ignition using indirect-drive targets on the National Ignition Facility,” Phys. Plasmas 11, 339 (2004).
J. G. Linhart et al., “Amplification of magnetic fields and heating of plasma by a collapsing metallic shell,” Nucl. Fusion Suppl. 2, 733 (1962); https://www.osti.gov/biblio/4726225.
J. P. Knauer et al., “Compressing magnetic fields with high-energy lasers,” Phys. Plasmas 17, 056318 (2010).
J. R. Davies et al., “Laser-driven magnetized liner inertial fusion,” Phys. Plasmas 24, 062701 (2017).
P. Y. Chang et al., “Fusion yield enhancement in magnetized laser-driven implosions,” Phys. Rev. Lett. 107, 035006 (2011).
S. A. Slutz et al., “Pulsed-power-driven cylindrical liner implosions of laser preheated fuel magnetized with an axial field,” Phys. Plasmas 17, 056303 (2010).
M. R. Gomez et al., “Experimental demonstration of fusion-relevant conditions in magnetized liner inertial fusion,” Phys. Rev. Lett. 113, 155003 (2014); “Performance scaling in magnetized liner inertial fusion experiments,” 125, 155002 (2020).
L. J. Perkins et al., “The potential of imposed magnetic fields for enhancing ignition probability and fusion energy yield in indirect-drive inertial confinement fusion,” Phys. Plasmas 24, 062708 (2017).
J. D. Moody et al., “Transient magnetic field diffusion considerations relevant to magnetically assisted indirect drive inertial confinement fusion,” Phys. Plasmas 27, 112711 (2020).
A. Engwall et al., U.S. Patent Application No. 62/928968 (October 31, 2019) Lawrence Livermore National Security, LLC, “High-resistivity metal alloy coatings fabricated with physical vapor deposition” LLNL reference: IL-13488.
L. B. Bayu Aji et al., “Sputtered Au–Ta films with tunable electrical resistivity,” J. Phys. D 54, 075303 (2020).
O. A. Hurricane et al., “Beyond alpha-heating: driving inertially confined fusion implosions toward a burning-plasma state on the National Ignition Facility,” Plasma Phys. Control. Fusion 61, 014033 (2018).
P. F. Schmit et al., “Understanding fuel magnetization and mix using secondary nuclear reactions in magneto-inertial fusion,” Phys. Rev. Lett. 113, 155004 (2014); P. F. Knapp et al., “Effects of magnetization on fusion product trapping and secondary neutron spectra,” Phys. Plasmas 22, 056312 (2015).
K. L. Baker et al., “High-performance indirect-drive cryogenic implosions at high adiabat on the National Ignition Facility,” Phys. Rev. Lett. 121, 135001 (2018).

About the Author

Dr. John D. Moody is from San Jose, California, and is currently a senior scientist in the National Ignition Facility and Inertial Confinement Fusion program at Lawrence Livermore National Laboratory (LLNL). He received a B.A. in physics from the University of California, Berkeley, in 1982 and a Ph.D. in plasma physics from the Massachusetts Institute of Technology in 1988, where he studied ion Bernstein wave heating on the Alcator C tokamak. After a postdoc studying pure electron plasmas at the University of California, San Diego, and a second postdoc at LLNL, he became a staff scientist at LLNL. He is a fellow of the American Physical Society. Some of his current interests include basic physics in ultrahigh magnetic fields, magnetized HED science, and plasma ignition science.