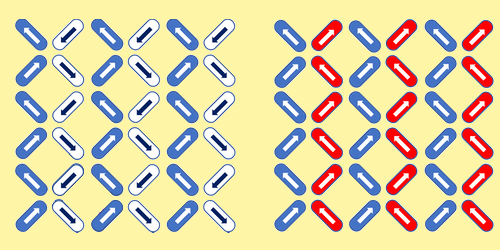
1D Random-Field Ising Model Experimentally Realized
The 1D random-field Ising model (1D-RFIM) is, for many, the go-to model for approximating avalanche phenomena in systems ranging from granular materials to electrical circuits. But most of the systems approximated by the model are 2D or 3D, and the results and predictions don’t always match. Now, Peter Schiffer of Yale University, Karin Dahmen of the University of Illinois at Urbana-Champaign, and colleagues show that they can accurately realize the 1D model in an artificial spin ice (ASI) [1]. Schiffer says that their experimental demonstration could allow for better modeling of more complex avalanching systems.
ASIs—systems that consist of nanomagnets arranged on a lattice—can exhibit avalanche behavior when the magnetic moments of clusters of magnets suddenly flip direction in quick succession. This process is triggered by applying external magnetic fields to the ASI, but it can be hard to control. Looking to better manipulate avalanching in this system, Schiffer and his colleagues designed an ASI where the flipping dynamics follow that of the 1D model as closely as possible.
The team’s ASI comprises a 2D array of rod-shaped magnets arranged on a square lattice. The ASI started off in its collective ground state, where the magnets in each column shared a single alignment, opposite to that of the columns on either side. They then applied a series of magnetic fields to the system and measured the moments of the magnets with a magnetic force microscope.
Analyzing the sizes of the resulting avalanches along the columns, the team found that they directly matched those predicted by the 1D-RFIM. The team says that the analysis framework they developed should also be applicable to other systems that exhibit avalanche behavior.
–Katherine Wright
Katherine Wright is the Deputy Editor of Physics Magazine.
References
- N. S. Bingham et al., “Experimental realization of the 1D random field Ising model,” Phys. Rev. Lett. 127, 207203 (2021).