An Efficient Way to Predict Water’s Phases
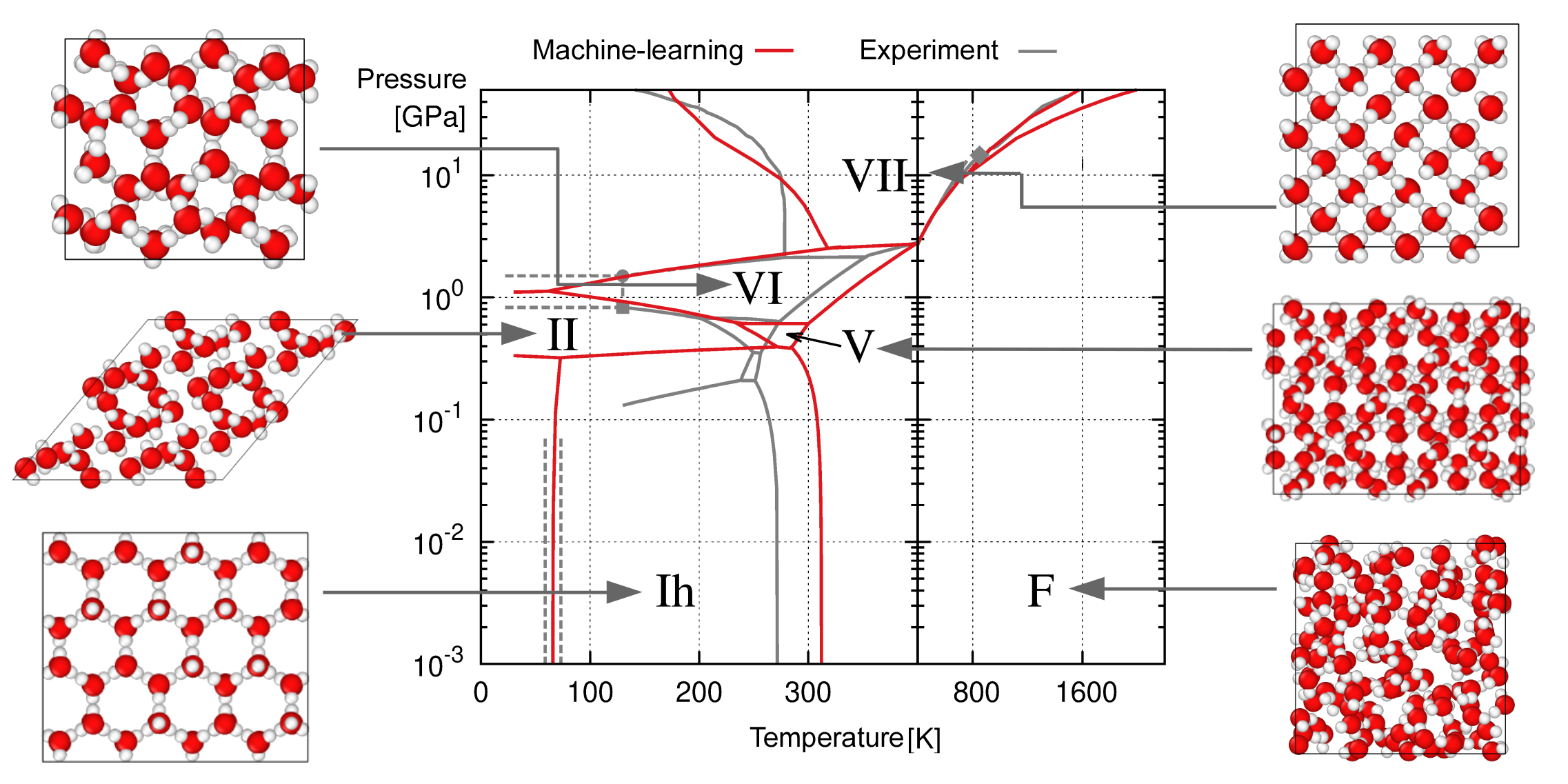
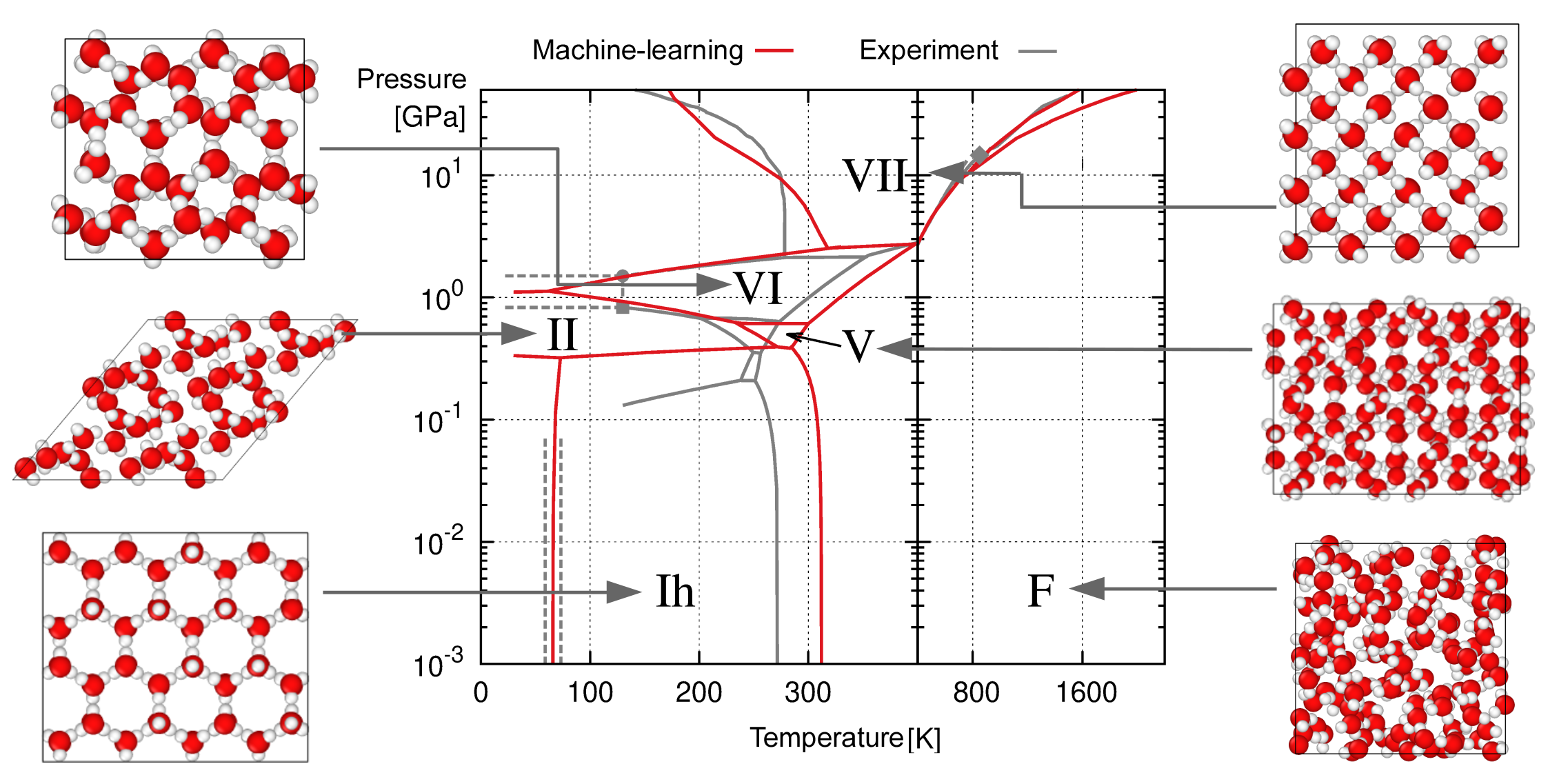
Given its familiarity, water is a surprisingly tricky substance to simulate. In addition to having liquid and gas phases, water adopts at least 14 distinct solid configurations—in both molecular and ionic forms—depending on the temperature and pressure. This complex phase space makes water an ideal testbed for theoretical models that predict material behaviors. Now, researchers have tested an efficient new model and found that it can predict all of water’s phases with an accuracy approaching that of much more computationally demanding techniques [1].
The first step in mapping a material’s phase space is to construct its “potential energy surface” (PES) under various conditions. The PES describes the probability of finding a specific configuration at a given temperature and pressure. The gold standard way to approach this task is to use ab initio calculations, which capture the quantum-mechanical behavior of the system’s electrons. But the computational cost of this method is so high that simulating more than a narrow range of conditions is impractical. So far, the majority of water’s phase space has been mapped using quicker, less reliable approximations.
Linfeng Zhang at Princeton University and colleagues achieve both accuracy and speed by using carefully selected ab initio calculations to train a machine-learning algorithm. Beginning with a rough phase diagram based on experimental data, the algorithm identifies points on the map where ab initio calculations are most needed. After performing these calculations, the process repeats until the error in the approximation falls below an acceptable threshold.
The researchers plan to use the technique to map parts of water’s phase space that are uncharted by experiment. They also say that future applications could include nuclear quantum effects on water’s various properties.
–Marric Stephens
Marric Stephens is a Corresponding Editor for Physics Magazine based in Bristol, UK.
References
- L. Zhang et al., “Phase diagram of a deep potential water model,” Phys. Rev. Lett. 126, 236001 (2021).