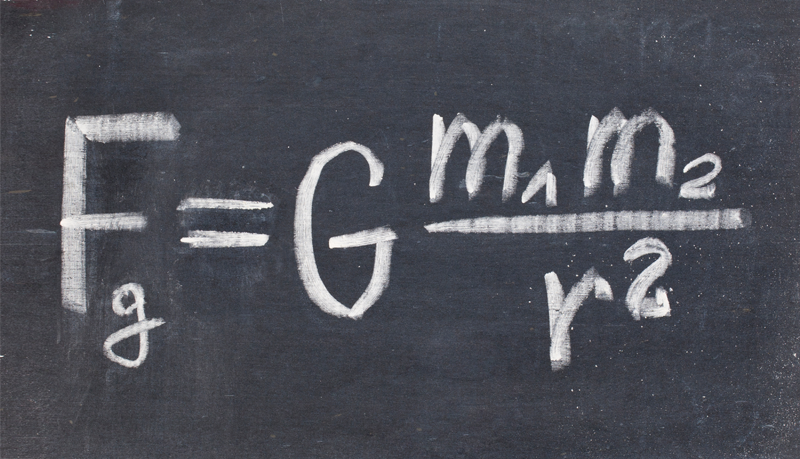Bending under Big G
Newton’s constant of gravity, or “big G” as it is called, is one of the oldest physical constants but also one of the least precisely measured. A new experiment tucked under the Swiss Alps has demonstrated a new technique for measuring G by tracking the undulations of two long metal beams [1]. The results at 40 Hz—the highest frequencies ever probed in G measurements—could help sort out discrepancies in experiments at low or zero frequencies. To improve the precision of their metal-beam experiment, the researchers are working on follow-up measurements with spinning beams.
According to Newton’s theory, the gravitational force between two objects is equal to G multiplied by their masses and divided by their distance squared. Big G was first measured rigorously in 1798 by Henry Cavendish who used a torsion pendulum to observe the attraction between metal spheres. Subsequent G measurements have usually been variations on the torsion pendulum scheme, but surprisingly the values have not always overlapped (see Synopsis: An Uncertain Big G). The explanation is that there are hidden uncertainties—or systematic errors—that are plaguing the experiments, so researchers are considering new measurement techniques that might eliminate these errors.
One way to change things up is to measure G in a dynamic situation rather than in the traditional situation where test masses are held static or oscillated at small frequencies. Going to higher frequencies can increase the energy flow between test masses and reduce a form of noise called 1∕f noise. Recently, several groups have probed gravity at high frequencies, but until now these experiments have not been able to measure G or to capture some aspects of gravity, such as the distance dependence. “We have been able to show a fully characterized experiment regarding gravity at a frequency far above what everybody else has done,” says Jürg Dual from the Swiss Federal Institute of Technology (ETH) in Zurich.
Performing a dynamic experiment gives the advantage that one is not at the mercy of gravitational-field inhomogeneities that may influence a static experiment. Dual gives the hypothetical example of a heavy cannonball fired over a century ago and now embedded in the ground underneath a laboratory. “That hidden cannonball might actually influence your experiment,” he says. But since gravitational sources like this are typically not moving, they won’t disturb measurements made at a specific frequency.
For their dynamical experiment, Dual and his colleagues built a gravitational “transmitter” and “detector” using 1-m-long beams encased in separate vacuum chambers. The beams are suspended by wires from a support, allowing them to bend back and forth horizontally. The 4-kg transmitter beam is made of tungsten, while the detector beam is made of titanium and weighs 1/6th as much. The researchers tailored the detector to be a very good resonator at 40 Hz, which means that it will respond to any kind of input at that frequency—be it sound waves or temperature variations. Because of that sensitivity to noise, the researchers performed their experiment in a former fortress carved into a mountain, isolated from rambling trucks and weather changes.
To measure G, the team used a small transducer to move the middle of the transmitter beam back and forth by a millimeter or so. The resulting change in the transmitter’s shape caused the gravitational force on the detector beam to oscillate. The detector responded by wiggling back and forth with an amplitude of around 10 pm as determined by laser interferometry. By varying the distance between the beams from 60 to 120 mm, the researchers were able to detect an “inverse square law” as predicted by Newton’s theory. This observation confirmed that the detector’s response depended on the gravitational force between the beams.
The data also provided a measurement of G, which was within 2% of the accepted value. Dual says that measuring G at 40 Hz could have potential implications for interpreting gravitational-wave data from detectors, such as the Laser Interferometer Gravitational-Wave Observatory (LIGO), that operate at similar frequencies (around 100 Hz). For example, his group is considering experiments that could test whether gravitational waves can be attenuated by matter along the wave path.
“The experiment is a very interesting work to probe G at other frequencies,” says Shan-Qing Yang from Sun Yat-sen University in China. Yang was involved in a recent set of torsion-pendulum experiments that achieved record-setting precision (11 parts per million) in a G measurement. By contrast, the error in the metal-beam experiment is much higher (1.7%). Yang says that a lot of effort will be needed to reduce the uncertainty. The team is already at work improving their experiment by including two transmitter rods that rotate in a synchronous pattern. This movement results in a larger variation in the distance between mass elements, and thus the detector beam experiences a larger variation in gravitational forces. Dual says that this setup should increase the amplitude of the detector wiggles by a factor of 10 to 50. The mathematical modeling of this spinning system is more complicated, but “we are working on that,” he says.
–Michael Schirber
Michael Schirber is a Corresponding Editor for Physics Magazine based in Lyon, France.
References
- T. Brack et al., “Dynamic measurement of gravitational coupling between resonating beams in the hertz regime,” Nat. Phys. (2022).