Sizing Up the Potential of Quantum Batteries

Sourav Bhattacharjee

Viewpoint

Sizing Up the Potential of Quantum Batteries

Indian Institute of Technology, Kanpur, Kanpur-208016, Uttar Pradesh, India

April 4, 2022• Physics 15, 50

A new study has quantified the maximum speedup of a battery’s charging time that can be achieved through quantum effects.

Figure caption — **Figure 1:** Sketches of the flow of energy (blue) from a source to a battery made up of multiple cells. (left) In a classical battery, in which each cell is charged independently, the charging speed scales linearly with the number of cells, L. (right) In a quantum battery, the collective charging of multiple entangled cells can scale quadratically with L, implying a potentially significant speedup compared to a classical battery.

Modern-day batteries have seen dramatic improvements in their capacity and charging speeds. However, with the progressive miniaturization of electronics, researchers have started to explore whether quantumness can be a resource for improving battery technology. Recent work, for instance, has suggested that quantum effects, from coherence to entanglement, could one day be harnessed to build “quantum batteries” whose charging speeds may exceed those of their classical counterparts. So far, however, an exact theoretical estimation of how large this speedup can be was lacking. Now, Ju-Yeon Gyhm of the Institute of Basic Science in the Republic of Korea and colleagues prove that the charging speed of quantum batteries can scale at most quadratically with the number of cells making up the battery [1]. This quadratic scaling implies a potentially large quantum advantage over classical batteries, whose charging speed scales linearly with the number of cells.

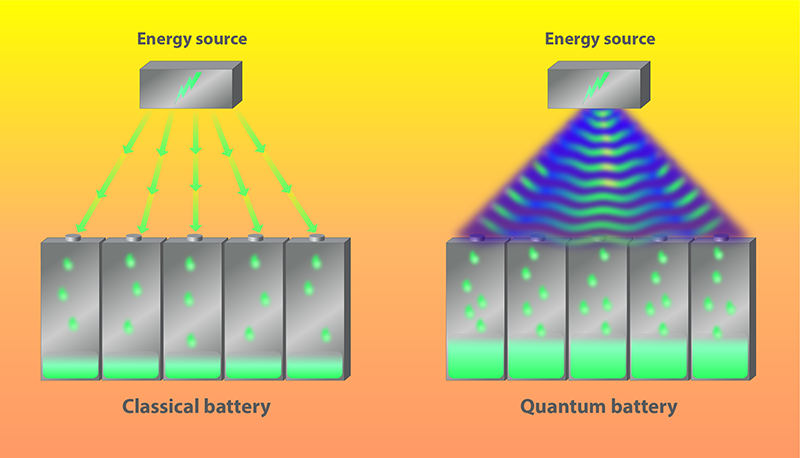
The linear scaling of the charging speed in conventional multicellular batteries, such as those used in our cars, is a fundamental limit set by classical charging techniques. The linear scaling stems from the fact that battery cells are typically charged in parallel, meaning that each cell is charged independently of the others. This scaling does not necessarily apply to quantum batteries in which the charging protocol couples multiple cells in the battery (Fig. 1). Recent theoretical studies showed that a faster-than-linear scaling, inconceivable for classical batteries, could be achieved thanks to a quantum entanglement involving multiple cells [2, 3].

Theoretically, a quantum battery can be modeled as a collection of simple quantum systems, such as an ensemble of spin- $\frac{1}{2}$ particles placed in a magnetic field, with each spin representing an individual cell. In this model, the charging process is described as the time-dependent response of the system to an external perturbation, which leads to the injection of energy into the battery. The external perturbation, which can take the form of an additional magnetic field perpendicular to the initial one, is switched off when the desired energy has been delivered, completing the charging process. The energy stored in a quantum battery at a given time is computed with respect to the “bare” Hamiltonian that describes the unperturbed system. The “charging” Hamiltonian describes the system with the addition of the external perturbation that orchestrates the energy infusion into the battery during charging.

If each spin gains energy independently without interacting with other spins, as in the charging example above, the quantum model describes a “parallel” charging protocol. “Collective” charging protocols instead couple different cells by generating entanglement among the cells. Researchers realized that this entanglement, which has no classical analogue, might imply a charging speedup over classical protocols [4–7]. In the quantum case, an uncharged battery corresponds to a system in the ground state of the bare Hamiltonian. As the battery charges, the system’s wave function develops an overlap with higher energy eigenstates. At a given time, the charging speed depends on how spread out the wave function is among the excited states. (This spreading is quantified by the “variance” of the bare Hamiltonian operator calculated over the evolved wave function). If the battery cells are entangled, the variance—hence the charging speed—can grow faster than linearly with the number of cells [7].

To assess the technological potential of quantum batteries, it would be important to know whether there is an upper limit to the scaling of the charging rate and under what conditions this optimal scaling would be achieved. So far, exact analytical derivations failed to find such an upper limit. In 2020, however, a numerical search by the team of Davide Rossini of the University of Pisa [8] found that the charging rate can scale quadratically if all-to-all-coupled cells are charged collectively. Since this case is an extreme scenario of collective charging, it is reasonable to expect that this quadratic scaling would be the maximum achievable scaling. But a rigorous analytical proof of this conclusion was lacking.

Gyhm and colleagues have now delivered such a proof. The first crucial step of their derivation is the demonstration that the charging speed is limited by the ability of the charging Hamiltonian to couple eigenstates of the bare Hamiltonian that have substantially different energies. If the charging Hamiltonian can couple pairs of eigenstates whose energy eigenvalues differ by less than $Δ E$ , switching on the external perturbation would cause the wavefunction to rapidly spread out among all the eigenstates whose energies lie within a range $Δ E$ of the ground- state energy. It would instead take a longer time to spread among states outside of that range. Thus, a higher value of $Δ E$ would facilitate a faster spreading and consequently a faster charging rate. The researchers show mathematically that the maximal charging rate is proportional to $Δ E$ multiplied by the operator norm of the charging Hamiltonian. For a quantum battery model, this norm—defined as the highest energy eigenvalue of the Hamiltonian—would scale at most linearly with the number of cells, L.

The second step of the team’s derivation is to prove that $Δ E$ is proportional to the maximum number of cells, k, coupled by the charging Hamiltonian. Thus, when a battery with L cells is charged in parallel, that is, $k = 1$ , the charging power scales with the charging Hamiltonian’s operator norm, so this scaling can be at best linear with L. In the collective charging situation, in which all cells are charged collectively, $k = L$ , and the maximal charging speed scales as $L^{2}$ .

This result finally puts to rest the question of the maximal possible scaling of the charging speed in quantum batteries. However, the road to the practical realization of quantum batteries remains a long one, given the fact that the systems analyzed theoretically so far are at best simplified toy models, which neglect, among other things, energy leakages into the environment and losses associated with the coupling of the battery to energy sources or sinks. What’s more, collective charging may have detrimental side effects. For instance, a higher variance of the bare Hamiltonian would imply fluctuations in the battery energy output, which could be hazardous to circuits connected to the battery. Prior studies have also indicated that entanglement can limit the fraction of the stored energy that can be recovered from the battery for later use [9, 10]. Nevertheless, the upper bound derived by Gyhm and colleagues will be a useful reference for researchers racing to demonstrate experimentally a quantum speedup over classical batteries.

References

J.-Y. Gyhm et al., “Quantum charging advantage cannot be extensive without global operations,” Phy. Rev. Lett. 128, 140501 (2022).
R. Alicki and M. Fannes, “Entanglement boost for extractable work from ensembles of quantum batteries,” Phys. Rev. E 87, 042123 (2013).
S. Bhattacharjee and A. Dutta, “Quantum thermal machines and batteries,” Eur. Phys. J. B 94, 239 (2021).
K. V. Hovhannisyan et al., “Entanglement generation is not necessary for optimal work extraction,” Phys. Rev. Lett. 111, 240401 (2013).
F. Campaioli et al., “Enhancing the charging power of quantum batteries,” Phys. Rev. Lett. 118, 150601 (2017).
F. C. Binder et al., “Quantacell: Powerful charging of quantum batteries,” New J. Phys. 17, 075015 (2015).
S. Julià-Farré et al., “Bounds on the capacity and power of quantum batteries,” Phys. Rev. Research 2, 023113 (2020).
D. Rossini et al., “Quantum advantage in the charging process of Sachdev-Ye-Kitaev batteries,” Phys. Rev. Lett. 125, 236402 (2020).
G. M. Andolina et al., “Extractable work, the role of correlations, and asymptotic freedom in quantum batteries,” Phys. Rev. Lett. 122, 047702 (2019).
D. Rossini et al., “Many-body localized quantum batteries,” Phys. Rev. B 100, 115142 (2019).

About the Author

Sourav Bhattacharjee works on a diverse set of fields at the interface of quantum thermodynamics, quantum information, quantum chaos theory, and topological systems. His research interests include the theoretical investigations of quantum heat engines and quantum batteries as well as the study of the propagation and stability of topological edge states, quantum correlations and information in presence of environmental dissipation. At present, he is investigating the manifestation of quantum chaos in periodically driven systems. Sourav received his master’s degree from the Indian Institute of Technology, Kanpur, where he is now pursuing a Ph.D. in physics.