Liquid-Metal Flows Show Surprising Heat Transport Behavior
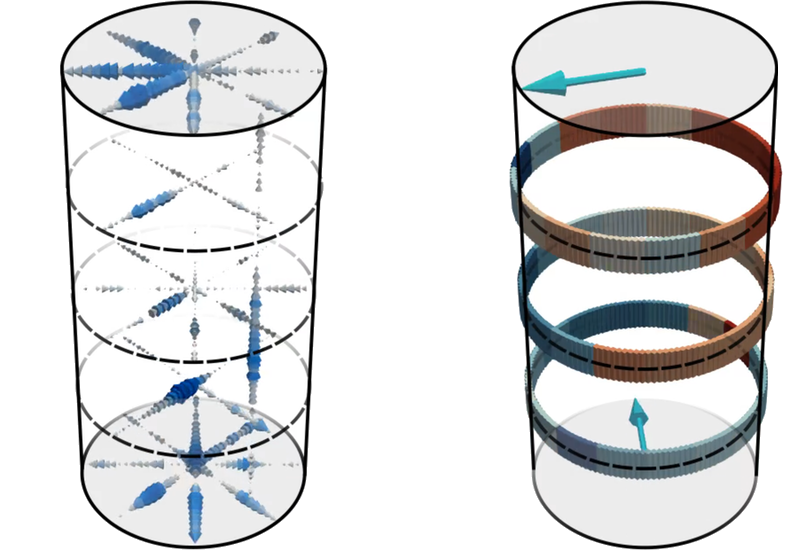
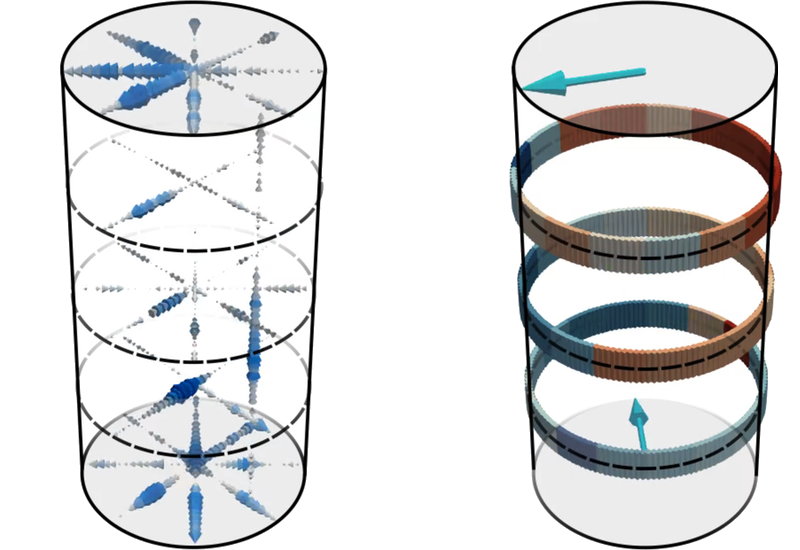
Temperature-induced liquid-metal flows, such as the molten-metal flows of Earth’s inner core, show surprising thermal properties, according to new experiments [1]. These experiments reveal that a liquid metal driven vigorously by buoyancy exhibits a flow transition at high turbulence intensities to a highly volatile state with lower heat transport efficiency (Fig. 1). Such a decrease in the heat transport is unpredicted by any existing theories [2]. The new findings could help researchers develop sophisticated models of the dynamo in Earth’s interior, design more efficient renewable liquid-metal batteries, and improve the design of nuclear fusion vessels.
Felix Schindler of the Helmholtz-Zentrum Dresden-Rossendorf, Germany, and colleagues performed experiments on so-called Rayleigh-Bérnard convection, which is relevant to numerous heat transfer phenomena . They used a liquid-metal alloy composed of gallium, indium, and tin, which was placed in a vertical cylindrical cell between two plates and then heated from below and cooled from above. Hot liquid rising from the bottom of the cell and cold liquid descending from the top drove a horizontal shear near the plates that set up a large-scale circulation (LSC) in the liquid metal—a mean flow that rises vertically on one side of a cylinder and descends vertically on the opposite side [3]. This large-scale motion resembles a race between cyclists starting from opposite ends of a velodrome.
An important goal of these experiments is to determine the rate at which heat rises from the hot bottom plate to the cold top plate with increasing convection strength, a parameter that characterizes the upward buoyancy force. Models often presume that this upward heat transfer rate increases approximately as a power law at the very large convection strengths relevant for many geophysical, astrophysical, and engineering applications.
The convection strength of the flow depends both on the temperature difference across the cell and on the height of the cell, with bigger temperature differences and larger cell heights leading to higher convection strengths. But in experiments, increasing the convection strength by increasing cell height means decreasing the cylinder’s diameter-to-height aspect ratio, which can disrupt the LSC and decrease the heat flow [4]. Flows in liquid metals are particularly sensitive to cell aspect ratio, as liquid metals diffuse heat more readily than momentum, meaning that their heat transport depends more acutely on the LSC [5, 6].
Schindler and colleagues explore this interplay between convection strength and cell aspect ratio in their experiments by using two different cylindrical cells. One cell had an aspect ratio of unity and the other an aspect ratio of one half. They performed a series of experiments for each cell, increasing the temperature difference between the bottom and top plates of the cell for each new run. For each of these runs, they simultaneously measured the temperatures and velocity field of the system.
The design of the experiments gave the team direct access to details of the LSC that were missing in previous experiments, which only involved temperature measurements [7–9]. Using cells with different aspect ratios also provided other benefits: First, using the slender cell (aspect ratio of one half), the team was able to achieve greater lateral confinement of the fluid than in other experiments. This confinement drastically reduced the LSC in the slender cell as compared to the wider cell (aspect ratio of unity) when the two systems had the same convection strength. The different LSCs in the two cells could then be correlated to the heat transfer measurements. Second, when the two cells had the same temperature difference between their plates, the convection strength in the slender cells was significantly higher—convection strength varies as the cube of cell height. It is not practical to keep increasing the temperature difference between the plates for a fixed cell height, so this ability to change the cell height gave the team access to higher convection strengths.
The team found that for the same convection strength, the slender cell had a significantly smaller LSC velocity compared with the wider cell, likely because of the greater lateral confinement of the liquid metal. They also found that under the same conditions, the large-scale flow was very different in the two cells: in the wider cell, the LSC mostly manifested as a single coherent roll of fluid between the bottom and top plates; in the slender cell, drastic and rapid transitions in the multirolled structures resulted in a disintegration of the LSC into an almost structureless state. Although in both cells the velocity of the LSC decreased with increasing convection strength, the transition to no LSC was only visible in the slender cell—the absence of the main heat flow pathway forced the hot rising liquid and the cold sinking liquid to “jam,” degrading the heat transfer efficiency. This collapse of the LSC was accompanied by a transition in the heat transport law to a previously unseen regime where the heat transport scaling exponent decreased from 0.221 to 0.124, marking a substantial slowdown in the rate at which heat rose. The wider cell did not display any such transition.
Despite their relevance for applications, liquid-metal studies are scarce compared with those in other fluids, such as air or water, because of experimental challenges: liquid metals are opaque, have high conductivities, and are cumbersome to handle. Simulations are also expensive because of resolution and run-time requirements [10]. Thus, the comprehensive level of detail provided by the new study of Schindler and colleagues is important beyond the finding of a new heat transport regime. That said, it is unclear whether the cell aspect ratio matters to the new results. If, in the wider cell, the LSC were to remain robust against increasing convection strength, it is possible that—being less constrained—the liquid metal might elude the transition. On the other hand, given that with increasing convection strength the top- and bottom-plate flows in the wider cell become increasingly uncorrelated, and the LSC velocity steadily declines in magnitude, it might be that a similar transition for the wider cell requires higher convection strengths. The new result is also at odds with previous work that reported comparable convection strengths for cells of aspect ratio one half [7, 8]. This variance will stimulate further studies, turning the spotlight on turbulent liquid-metal convection—an enticing prospect that the field deserves.
References
- F. Schindler et al., “Collapse of coherent large scale flow in strongly turbulent liquid metal convection,” Phys. Rev. Lett. 128, 164501 (2022).
- S. Grossmann and D. Lohse, “Thermal convection in small Prandtl number liquids: strong but ineffective,” AIP Conf. Proc. 1076, 68 (2008).
- T. Vogt et al., “Jump rope vortex in liquid metal convection,” Proc. Natl. Acad. Sci. U.S.A. 115, 12674 (2018).
- A. Pandey and K. R. Sreenivasan, “Convective heat transport in slender cells is close to that in wider cells at high Rayleigh and Prandtl numbers,” Europhys. Lett. 135, 24001 (2021).
- T. Zürner et al., “Combined measurement of velocity and temperature in liquid metal convection,” J. Fluid Mech. 876, 1108 (2019).
- L. Zwirner et al., “Elliptical instability and multiple-roll flow modes of the large-scale circulation in confined turbulent Rayleigh-Bénard convection,” Phys. Rev. Lett. 125, 054502 (2020).
- S. Cioni et al., “Strongly turbulent Rayleigh–Bénard convection in mercury: Comparison with results at moderate Prandtl number,” J. Fluid Mech. 335, 111 (1997).
- J. A. Glazier et al., “Evidence against ‘ultrahard’ thermal turbulence at very high Rayleigh numbers,” Nature 398, 307 (1999).
- E. M. King and J. M. Aurnou, “Turbulent convection in liquid metal with and without rotation,” Proc. Natl. Acad. Sci. U.S.A. 110, 6688 (2013).
- J. D. Scheel and J. Schumacher, “Predicting transition ranges to fully turbulent viscous boundary layers in low Prandtl number convection flows,” Phys. Rev. Fluids 2, 123501 (2017).