Laughlin’s Charge Pump Realized
Periodic boundary conditions are an indispensable tool in theoretical studies, allowing researchers to not only simplify calculations but also to explore profound concepts. Imagining how to implement these boundary conditions in physical systems can be especially fruitful. A prototypical example is a 1981 thought experiment devised by the Nobel-prize-winning physicist Robert Laughlin to explain the quantization of Hall conductance [1]. This thought experiment introduced the idea of Laughlin’s charge pump, which has so far remained unrealized. Now, Aurélien Fabre, from the Kastler Brossel Laboratory, France, and his colleagues have created a “synthetic Hall cylinder” for dysprosium atoms that realizes Laughlin’s charge pump, allowing the team to experimentally observe features of this system [2].
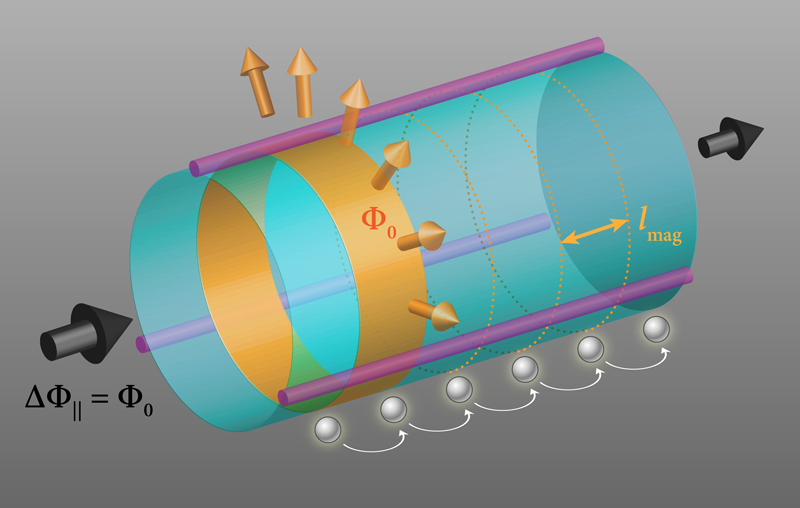
In his thought experiment, Laughlin considered quantum Hall states on a cylinder whose surface and two ends are penetrated by finite magnetic fluxes. Laughlin argued that changing the axial magnetic flux would result in a current along the axial direction such that charges would be pumped along the cylinder’s surface. The most important characteristic of Laughlin’s charge pump is that it is topological: If the rate of change of the axial flux is slow enough for the system to be adiabatic, the details of its time dependence don’t matter—the number of pumped electrons always increases by an integer number when the axial flux changes by one quantum.
Soon after Laughlin’s proposal, physicist David Thouless developed a closely related idea to describe topological charge pumping in generic systems, in which some parameter changes slowly and periodically [3]. Whereas the Thouless pump has been demonstrated in laboratories using ultracold atoms in optical lattices [4, 5], realizing Laughlin’s scheme has proved more difficult because of the need for periodic boundary conditions. Like most physical systems available in laboratories, the Hall bars that physicists use to study quantum Hall states have open boundaries. And while there exist systems with periodic boundary conditions—such as carbon nanotubes—it is challenging to thread the necessary finite magnetic fluxes through their cylindrical surfaces.
Recent developments in atomic, molecular, and optical physics have provided physicists with an alternative route to study topological charge pumps and many other topological quantum phenomena. In such schemes, instead of driving the cyclotron motion of electrons using magnetic fields, as in Laughlin’s thought experiment, researchers use atom-laser interactions to generate “synthetic” magnetic fields that give rise to cyclotron motions of charge-neutral atoms [6]. Furthermore, atoms’ internal degrees of freedom, such as their hyperfine spins or electronic spins, can be used to represent a spatial dimension, with this or other synthetic dimensions allowing experimentalists to explore novel phenomena unattainable in conventional apparatuses (see Viewpoint: Photons Get Slippery) [7]. For instance, cyclically coupled hyperfine spins or electronic spins result in a periodic boundary condition in the synthetic dimension that mimics a periodic boundary condition in the spatial dimension. In 2018, two groups demonstrated such synthetic Hall cylinders. One group realized a synthetic Hall cylinder for fermionic ytterbium atoms and observed different band structures under boundary conditions in the synthetic dimension [8]. The other group created a synthetic Hall cylinder for bosonic rubidium atoms and discovered symmetry-protected band crossings, with the atoms requiring two periods to return to their original states in a Bloch oscillation [9].
In their new experiment, Fabre and colleagues create a synthetic dimension by coupling three electronic spin states of dysprosium atoms using two counterpropagating laser beams. One of the lasers has two frequency components, each of which prompts a Raman transition in combination with the other laser. One Raman transition flips the electronic spin by one quantum ( ), while the other Raman transition flips the electronic spin by two quanta ( ) . These three states thus form a cyclically coupled loop ( ), representing a one-dimensional lattice with a periodic boundary condition.
To demonstrate Laughlin’s charge pump, this setup requires an extra ingredient that previous experiments have not yet realized: The axial magnetic flux needs to be accurately controlled to reach the adiabatic limit. If the axial flux changes too fast compared with the energy difference between the atoms’ ground and excited states, the pumped charge no longer changes by an integer when the axial flux changes by one quantum. Fabre and colleagues achieve this condition by using laser beams to impose two phases—one position-dependent, one position-independent—to the intersite tunnelings in the synthetic dimension. The position-dependent phase gives rise to a net synthetic magnetic flux penetrating the cylindrical surface. The position-independent phase determines the axial magnetic flux. The researchers change the axial magnetic flux by tuning the laser phase and find that such a change leads to a displacement of the atomic cloud in the real dimension. They also vary the ramping rate of the laser phase and find that, when the ramping rate is slow enough, the displacement becomes linearly dependent on the change of the axial magnetic flux. The slope perfectly agrees with Laughlin’s prediction, confirming that the atomic cloud is pumped by one magnetic length once the axial magnetic flux changes by one quantum adiabatically.
This first experimental realization of Laughlin’s charge pump raises the possibility of many exciting developments. Although the three synthetic-dimension sites demonstrated fulfill the minimum requirement of a periodic boundary condition, enlarging the cylinder—for example, by including all 17 electronic states available to dysprosium atoms—could reduce finite-size effects. Furthermore, it would be interesting to generalize Laughlin’s charge pump to the strong atom-atom-interaction regime, where charge fractionalization is expected. Fabre and colleagues found that the system’s lowest few energy bands are flat, with bandwidths much narrower than the gaps between them. Interatom interactions become dominant in such flat bands, which could lead to the rich physics of fractional quantum Hall states or of fractional Chern insulators. In addition, it should be possible to explore systems with more complex synthetic topologies, such as a torus [10]. Putting quantum Hall states on a toroidal topology could result in stable ground-state degeneracy, which, being immune to local perturbations, would be useful for fault-tolerant quantum computing.
References
- R. B. Laughlin, “Quantized Hall conductivity in two dimensions,” Phys. Rev. B 23, 5632 (1981).
- A. Fabre et al., “Laughlin’s topological charge pump in an atomic Hall cylinder,” Phys. Rev. Lett. 128, 173202 (2022).
- D. J. Thouless, “Quantization of particle transport,” Phys. Rev. B 27, 6083 (1983).
- M. Lohse et al., “A Thouless quantum pump with ultracold bosonic atoms in an optical superlattice,” Nat. Phys. 12, 350 (2015).
- S. Nakajima et al., “Topological Thouless pumping of ultracold fermions,” Nat. Phys. 12, 296 (2016).
- Y.-J. Lin et al., “Synthetic magnetic fields for ultracold neutral atoms,” Nature 462, 628 (2009).
- A. Celi et al., “Synthetic gauge fields in synthetic dimensions,” Phys. Rev. Lett. 112, 043001 (2014).
- J. H. Han et al., “Band gap closing in a synthetic Hall tube of neutral fermions,” Phys. Rev. Lett. 122, 065303 (2019).
- C.-H. Li et al., “Bose-Einstein condensate on a synthetic topological Hall cylinder,” Phys. Rev. X Quantum 3, 010316 (2022).
- Y. Yan et al., “Emergent periodic and quasiperiodic lattices on surfaces of synthetic Hall tori and synthetic Hall cylinders,” Phys. Rev. Lett. 123, 260405 (2019).