Quantum Mechanics Must Be Complex
Complex numbers are widely exploited in classical and relativistic physics. In electromagnetism, for instance, they tremendously simplify the description of wave-like phenomena. However, in these physical theories, complex numbers aren’t strictly needed, as all meaningful observables can be expressed in terms of real numbers. Thus, complex analysis is just a powerful computational tool. But are complex numbers essential in quantum physics—where the mathematics (the Schrödinger equation, the Hilbert space, etc.) is intrinsically complex-valued? This simple question has accompanied the development of quantum mechanics since its origins, when Schrödinger, Lorentz, and Planck debated it in their correspondence [1]. But early on, the pioneers of quantum mechanics abandoned the attempt to develop a quantum theory based on real numbers because they thought it impractical. However, the possibility of using real numbers was never formally ruled out, and recent theoretical results suggested that a real-valued quantum theory could describe an unexpectedly broad range of quantum systems [2]. But this real-number approach has now been squashed by two independent experiments, performed by Ming-Cheng Chen of the University of Science and Technology of China [3] and by Zheng-Da Li of the Southern University of Science and Technology, China [4]. The two teams show that, within a standard formulation of quantum mechanics, complex numbers are indispensable for describing experiments carried out on simple quantum networks.
A basic starting point for quantum theory is to represent a particle state by a vector in a complex-valued space, called a Hilbert space. However, for a single, isolated quantum system, finding a description based purely on real numbers is straightforward: It can simply be obtained by doubling the dimension of the Hilbert space, as the space of complex numbers is equivalent, or “isomorphic,” to a two-dimensional, real plane, with the two dimensions representing the real and imaginary part of complex numbers, respectively. The problem becomes less trivial when we consider the unique quantum correlations, such as entanglement, that arise in quantum mechanics. These correlations can violate the principle of local realism, as proven by so-called Bell inequality tests [5]. Violations of Bell tests may appear to require complex values for their description [6]. But in 2009, a theoretical work demonstrated that, using real numbers, it is possible to reproduce the statistics of any standard Bell experiment, even those involving multiple quantum systems [2]. The result reinforced the conjecture that complex numbers aren’t necessary, but the lack of a general proof left open some paths for refuting the equivalence between “complex” and “real” quantum theories.
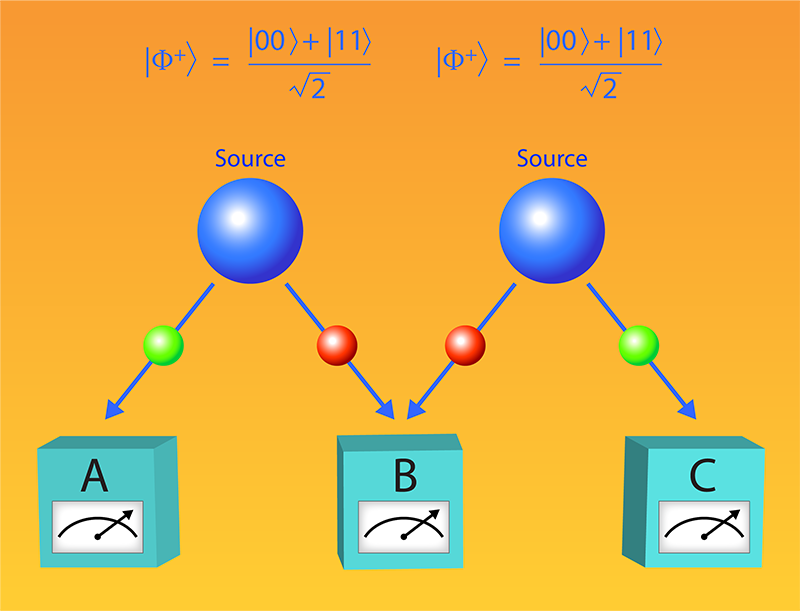
One such path was identified in 2021 through the brilliant theoretical work of Marc-Olivier Renou of the Institute of Photonic Sciences (ICFO) in Spain and co-workers [7]. The researchers considered two theories that are both based on the postulates of quantum mechanics, but one uses a complex Hilbert space, as in the traditional formulation, while the other uses a real space. They then devised Bell-like experiments that could prove the inadequacy of the real theory. In their theorized experiments, two independent sources distribute entangled qubits in a quantum network configuration, while causally independent measurements on the nodes can reveal quantum correlations that do not admit any real quantum representation.
Chen and colleagues and Li and colleagues now provide the experimental demonstration of Renou and co-workers’ proposal in two different physical platforms. The experiments are conceptually based on a “game” in which three parties (Alice, Bob, and Charlie) perform a Bell-like experiment (Fig. 1). In this game, two sources distribute entangled qubits between Alice and Bob and between Bob and Charlie, respectively. Each party independently chooses, from a set of possibilities, the measurements to perform on their qubit(s). Since the sources are independent, the qubits sent to Alice and Charlie are originally uncorrelated. Bob receives a qubit from both sources and, by performing a Bell-state measurement, he generates entanglement between Alice’s and Charlie’s qubits even though these qubits never interacted (a procedure called “entanglement swapping” [8]). Finally, a “score” is calculated from the statistical distribution of measurement outcomes. As demonstrated by Renou and co-workers, a complex quantum theory can produce a larger score than the one produced by a real quantum theory.
The two groups follow different approaches to implement the quantum game. Chen and colleagues use a superconducting quantum processor in which the qubits have individual control and readout. The main challenge of this approach is making the qubits, which sit on the same circuit, truly independent and decoupled—a stringent requirement for the Bell-like tests. Li and colleagues instead choose a photonic implementation that more easily achieves this independence. Specifically, they use polarization-entangled photons generated by parametric down-conversion and detected in superconducting nanowire single-photon detectors. The optical implementation comes, however, with a different challenge: The protocol proposed by Renou and co-workers requires a complete Bell-state measurement, which can be directly implemented using superconducting qubits but is not achievable exploiting linear optical phenomena. Therefore, Li and colleagues had to rely on a so-called “partial” Bell-state measurement.
Despite the difficulties inherent in each implementation, both experiments deliver compelling results. Impressively, they beat the score of real theory by many standard deviations (by 43 sigma and 4.5 sigma for Chen’s and Li’s experiments, respectively), providing convincing proof that complex numbers are needed to describe the experiments.
Interestingly, both experiments are based on a minimal quantum network scheme (two sources and three nodes), which is a promising building block for a future quantum internet. The results thus offer one more demonstration that the availability of new quantum technologies is closely linked to the possibility of testing foundational aspects of quantum mechanics. Conversely, these new fundamental insights on quantum mechanics could have unexpected implications on the development of new quantum information technologies.
We must be careful, however, in assessing the implications of these results. One might be tempted to conclude that complex numbers are indispensable to describe the physical reality of the Universe. However, this conclusion is true only if we accept the standard framework of quantum mechanics, which is based on several postulates. As Renou and his co-workers point out, these results would not be applicable to alternative formulations of quantum mechanics, such as Bohmian mechanics, which are based on different postulates. Therefore, these results could stimulate attempts to go beyond the standard formalism of quantum mechanics, which, despite great successes in predicting experimental results, is often considered inadequate from an interpretative point of view [9].
References
- C. N. Yang, “Square root of minus one, complex phases and Erwin Schrödinger,” Selected Papers II with Commentary (World Scientific, Hackensack, 2013)[Amazon][WorldCat].
- M. McKague et al., “Simulating quantum systems using real Hilbert spaces,” Phys. Rev. Lett. 102, 020505 (2009).
- M.-C. Chen et al., “Ruling out real-valued standard formalism of quantum theory,” Phys. Rev. Lett. 128, 040403 (2022).
- Z.-D. Li et al., “Testing real quantum theory in an optical quantum network,” Phys. Rev. Lett. 128, 040402 (2022).
- A. Aspect, “Closing the door on Einstein and Bohr’s quantum debate,” Physics 8, 123 (2015).
- N. Gisin, “Bell Inequalities: Many Questions, a Few Answers,” in Quantum Reality, Relativistic Causality, and Closing the Epistemic Circle, edited by W. C. Myrvold et al. The Western Ontario Series in Philosophy of Science, Vol. 73 (Springer, Dordrecht, 2009)[Amazon][WorldCat].
- M.-O. Renou et al., “Quantum theory based on real numbers can be experimentally falsified,” Nature 600, 625 (2021).
- J.-W. Pan et al., “Experimental entanglement swapping: Entangling photons that never interacted,” Phys. Rev. Lett. 80, 3891 (1998).
- T. Norsen, Foundations of Quantum Mechanics - An Exploration of the Physical Meaning of Quantum Theory, Undergraduate Lecture Notes in Physics (Springer, Cham, 2017)[Amazon][WorldCat].