Long-Range Quantum Cryptography Gets Simpler
The secure transmission of data is essential in our interconnected society but is constantly at risk as attackers keep seeking vulnerabilities and new methods to decrypt our messages. The emergence of quantum computers adds to the problem, as they hold the potential to break current encryption methods. A response to these threats is offered by quantum key distribution (QKD)—a cryptography technique exploiting the peculiar laws of quantum mechanics. In QKD, two remote users (Alice and Bob) exploit single photons to generate and exchange cryptographic keys with perfect security, as the activity of any eavesdropper would be spotted through changes in the photons’ quantum states. Photon losses, however, limit the speed and distance at which a QKD key can be transmitted, posing a barrier to applications. Some recently demonstrated protocols can in principle overcome these limitations, but at the price of impractically complicated setups. A series of studies, performed by the independent teams of Zhiliang Yuan of the Beijing Academy of Quantum Information and Jan-Wei Pan of the University of Science and Technology of China now shows the possibility of dramatic setup simplifications, removing the need for complex “phase-locking” schemes [1–3]. Yuan’s team’s solution, in particular, removes the need for even tracking the phase of the used lasers. It also achieves secure-key transmission up to 500 km at orders-of-magnitude-larger rates than previous demonstrations, approaching values of practical interest [1]. Together, these advances bode well for the transformation of QKD into a broadly available, commercial technology.
QKD—arguably the most mature among quantum technologies—works by exchanging photons between two users via optical fibers or free-space links. Among its biggest enemies are photon losses—due to scattering and absorption—which set the maximum operational distance over which signals aren’t trumped by noise. Alas, as of today there is no way to overcome these losses by regenerating signals: optical amplifiers like those used in classical networks would corrupt the quantum signals, while quantum repeaters won’t be available any time soon. Point-to-point QKD links over optical fibers have reached up to 421 km (See Viewpoint: Record Distance for Quantum Cryptography), but they have impractically low secure-key transmission rates [4].
In 2017, researchers derived a fundamental upper limit to the key-rate transmission of a point-to-point QKD scheme without repeaters (known as the “PLOB” bound from the initials of the paper’s authors) [5]. Ever since, however, researchers have proposed alternative QKD protocols that offer improvements in both security and reach without using repeaters. One such protocol, called measurement-device-independent QKD (MDI-QKD) involves Alice and Bob transmitting photons to an untrusted intermediary (Charlie) [6].
The use of this intermediary implies MDI-QKD can in principle bypass the PLOB bound. But an experimental challenge has so far prevented such a feat. Specifically, MDI-QKD relies on measuring a two-photon interference between photons sent by Alice and Bob and arriving at Charlie’s detectors in coincidence. Photon losses and other effects can make such coincident detections unlikely, lowering the secure-key transmission rate. To address this challenge, researchers proposed twin-field QKD (TF-QKD) in 2018 [7]. In TF-QKD, Alice and Bob transmit identical optical fields to Charlie, who measures the interference of fields rather than that of individual photons, eliminating the need for photon coincidence. Several experimental optical-fiber implementations of TF-QKD have indeed circumvented the PLOB bound, reaching 600 km in 2021 [8] and 1000 km in March of this year [9]. However, TF-QKD requires the fields generated by the two distant, independent light sources to be completely identical in every aspect, including their wavelength and the phase the fields acquire after propagation in the fiber. This locking of the system’s “global phase” can only be achieved with complex hardware and protocols that hinder applicability in most real-world scenarios. This phase locking usually requires the dissemination of a common optical frequency over long distances. A solution for removing this requirement, based on tracking the phase using optical frequency combs, appeared early this year [10]. The incorporation of frequency combs, however, still introduces significant complexities to the scheme.
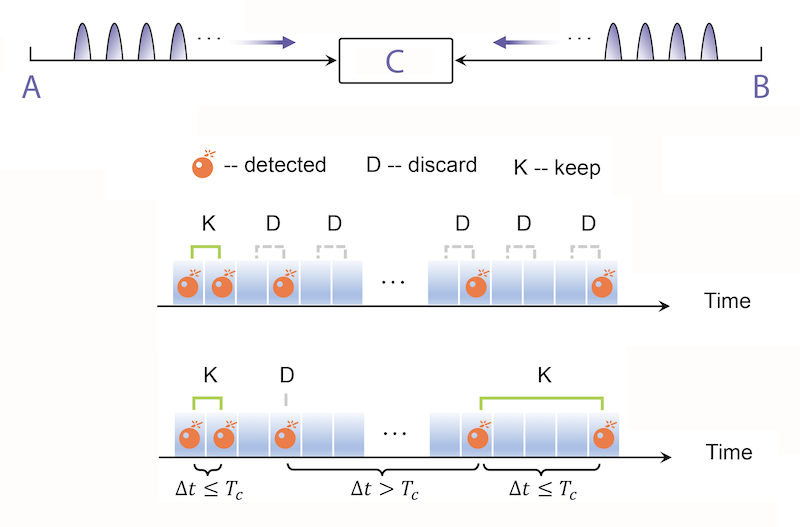
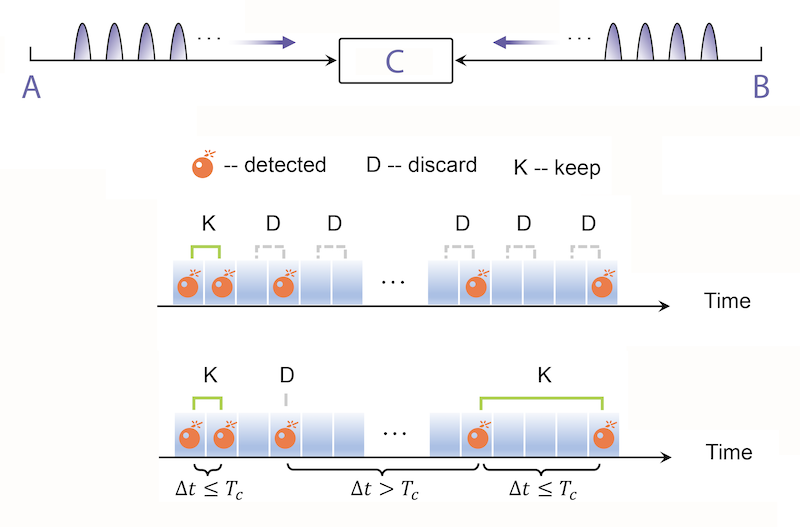
In 2022, two independent teams proposed to tackle this problem with a new approach, called post-measurement pairing QKD (PMP-QKD) [11, 12], that combines the best of the MDI- and TF-QKD worlds. The protocol is similar to MDI-QKD but alleviates the photon-coincidence demands. In standard MDI-QKD, photons are only usable if they arrive in two adjacent time bins. In PMP-QKD, Alice and Bob can “pair” their photons after detection, provided that such photons arrive within a so-called “pairing window,” whose width is determined by the fiber-induced phase fluctuations and by the rate at which the phases of the two lasers diverge ( Fig. 1). If this pairing window is sufficiently long, the number of usable photons is larger than that set by the PLOB bound.
Yuan’s team [1] and Pan’s team [2] demonstrated this PMP protocol experimentally. Both groups utilized a conventional MDI-QKD setup with two independent lasers, a central measurement station (Charlie), and no phase-locking mechanism. The key trick was to ensure a stable and predictable difference in the wavelengths of the two independent lasers, boosting their relative stability and hence the pairing window’s width. The teams exploit different laser technologies. Pan and colleagues employ commercial lasers with a narrow linewidth (about 2 kHz). They then interleave the photon sequences used for quantum communication with bright (classical) reference pulses used to estimate the wavelength difference. In other words, the team removed the need for “locking” the laser phases but “tracked” the phase through the reference pulses. Yuan and colleagues went a step further. They exploited state-of-the-art lasers with an exceptionally narrow (1-Hz) linewidth, which also eliminated the need to track the laser phases.
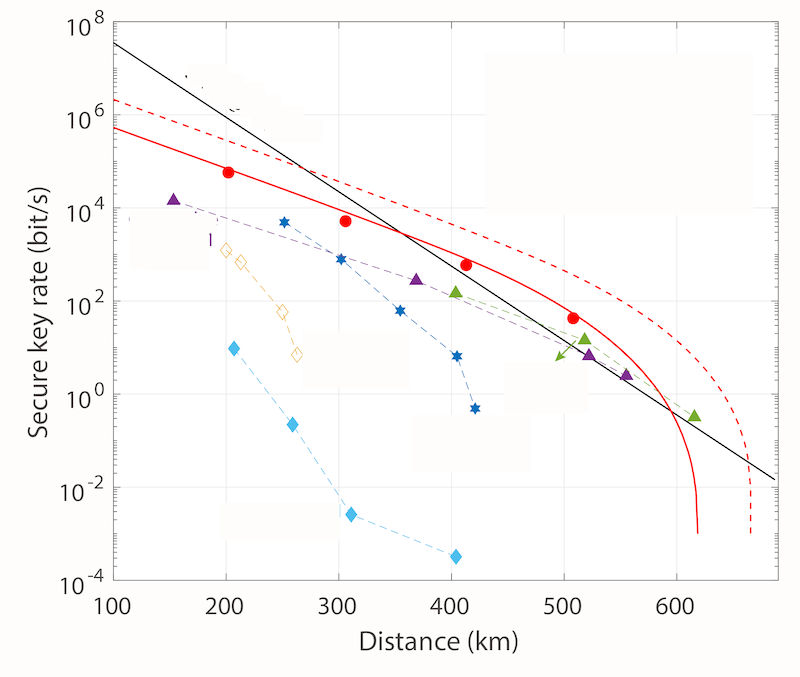
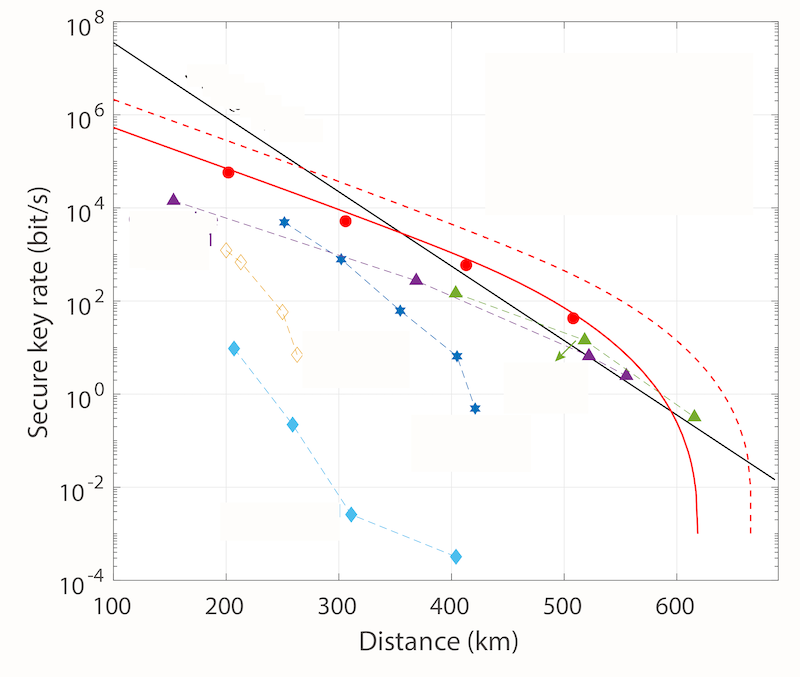
Pan’s team demonstrated a PMP enhancement up to 407 km of optical fibers but didn’t break the PLOB bound. Yuan’s group, on the other hand, clearly surpassed the PLOB bound at distances of 413 and 508 km, with rates of about 509 and 42 bits/s, respectively (Fig. 2). The 5 kbit/s rate they achieved at 306 km—a world’s record at this distance—would be sufficient to enable the real-time QKD encryption of voice communications with a secure technique known as one-time pad.
The PMP approach holds potential for wider applicability to other protocols, as shown in a recent study by Pan’s group [3]. The team applied a similar phase-estimation and tracking mechanism with bright reference pulses to a TF-QKD scheme. Using commercially available, 5-kHz-linewidth lasers and standard fiber, they surpassed the PLOB bound at 504 km without requiring global phase locking or active phase compensation at the receiver.
The new results show that there is great potential for QKD to become more practical. It is to be expected that there will be swift progress on several fronts—including simpler, less-expensive, and more efficient protocols and devices—which could dramatically boost QKD’s appeal for real-world applications.
References
- L. Zhou et al., “Experimental quantum communication overcomes the rate-loss limit without global phase tracking,” Phys. Rev. Lett. 130, 250801 (2023).
- H.-T. Zhu et al., “Experimental mode-pairing measurement-device-independent quantum key distribution without global phase locking,” Phys. Rev. Lett. 130, 030801 (2023).
- W. Li et al., “Twin-field quantum key distribution without phase locking,” Phys. Rev. Lett. 130, 250802 (2023).
- A. Boaron et al., “Secure quantum key distribution over 421 km of optical fiber,” Phys. Rev. Lett. 121, 190502 (2018).
- S. Pirandola et al., “Fundamental limits of repeaterless quantum communications,” Nat. Commun. 8, 15043 (2017).
- H.-K. Lo et al., “Measurement-device-independent quantum key distribution,” Phys. Rev. Lett. 108, 130503 (2012).
- M. Lucamarini et al., “Overcoming the rate–distance limit of quantum key distribution without quantum repeaters,” Nature 557, 400 (2018).
- M. Pittaluga et al., “600-km repeater-like quantum communications with dual-band stabilization,” Nat. Photon. 15, 530 (2021).
- Y. Liu et al., “Experimental twin-field quantum key distribution over 1000 km fiber distance,” Phys. Rev. Lett. 130, 210801 (2023).
- L. Zhou et al., “Twin-field quantum key distribution without optical frequency dissemination,” Nat. Commun. 14, 928 (2023).
- P. Zeng et al., “Mode-pairing quantum key distribution,” Nat. Commun. 13, 3903 (2022).
- Y.-M. Xie et al., “Breaking the rate-loss bound of quantum key distribution with asynchronous two-photon interference,” PRX Quantum 3, 020315 (2022).