Exceptional Sensing and Transport
In quantum mechanics, a system is conventionally described by a Hermitian Hamiltonian, whose solution gives the system’s energy states. Hermiticity is a mathematical property that guarantees various crucial characteristics of a quantum system. From a physical perspective, Hermiticity is required by the conservation of probability, which further stems from the assumption that the system of interest is in isolation. Conversely, when a system is open—meaning that it exchanges energy, particles, or information with the surrounding environment—it is no longer described by a Hermitian Hamiltonian. Over the past two decades, researchers have discovered numerous new phenomena and functionalities of open classical and quantum systems that have no analogs in conventional Hermitian systems, leading to the emerging research field of non-Hermitian physics [1]. In two separate experimental works, researchers have realized new non-Hermitian phenomena by taking advantage of a unique feature of non-Hermitian systems called an exceptional point [2, 3]. The first experiment utilized an exceptional point to amplify the signal of a magnetic field in an atomic gas. The second experiment demonstrated handedness, or chirality, in the transport of heat through a fluid system. These new works may open a new avenue toward actively controlling phases of matter.
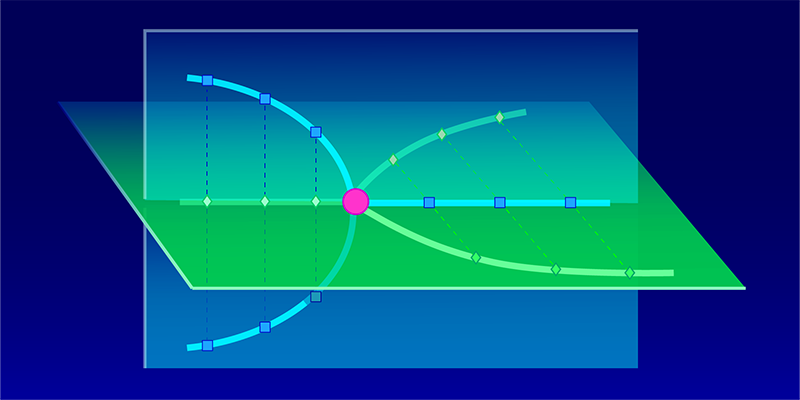
In closed systems governed by Hermitian Hamiltonians, states are always independent of each other, even if they possess the same spectrum. By contrast, in open systems characterized by non-Hermitian Hamiltonians, states can coalesce into a single state. This unique and unconventional spectral characteristic—referred to as an exceptional point—gives rise to exotic spectral singularities inherent in non-Hermitian systems and leads to a diverse range of physical phenomena in open systems [1, 4]. For example, an exceptional point accompanies spontaneous breaking of parity–time symmetry [5]. It is also noteworthy that an exceptional point underlies the theory of phase transitions in statistical mechanics [6].
The two new experimental works have harnessed the potential of exceptional points to advance physical applications. In the first experiment, a research group led by Yong-Chun Liu from Tsinghua University, China, used an exceptional point for magnetic-field sensing [2]. While a Hermitian system generally responds linearly to an input signal, a non-Hermitian system at an exceptional point typically generates a response proportional to the square root of the signal. For a small signal, such a square-root response is qualitatively larger than the conventional linear response, implying that the exceptional point can be leveraged to enhance the sensitivity of sensors [7]. While this sensitivity enhancement was previously demonstrated in optics and photonics [8], Liu’s team has accomplished it in a thermal atomic ensemble and thus extended its range of potential applications in atomic, molecular, and optical physics.
The researchers realized an exceptional point in a thermally interacting atomic gas, as was also done in previous studies [9]. Using a vapor cell of rubidium atoms, they prepared a multilevel thermal atomic ensemble and introduced non-Hermiticity via the manipulation of the decay rate of each energy level with a probe laser. The energy shared between the atoms is not conserved and escapes into another energy level—which acts as the surrounding environment. As a consequence of the interplay between the coherent coupling and the imbalanced decay rates for the different energy levels, the system exhibited an exceptional point. Specifically, the team observed it through the splitting of a resonance peak in the optical-polarization-rotation spectrum into two peaks as an input magnetic field was varied. The exceptional point makes the peak splitting sensitive to the magnetic field, thus offering an opportunity for the high-precision sensing.
From a practical viewpoint, it should be noted that an exceptional point amplifies not only a signal of interest but also noise, which can impede the sensitivity enhancement [10]. The scheme of Liu and colleagues aimed to overcome this challenge by relying on the optical-polarization-rotation signal. Further investigation should assess the general applicability of this new scheme and explore possible improvements to the scheme.
In the second experiment, Cheng-Wei Qiu from the National University of Singapore and collaborators explored direction-dependent, or chiral, thermal transport accompanied by an exceptional point [3]. They devised a fluid system in a cylinder involving two thin plates at the top and bottom that spin in opposite directions (clockwise and counterclockwise) and induce advection in each respective direction. Additionally, the sides of the cylinder are attached to heating and cooling sources that generate a thermal inflow. This fluid system is effectively described by a non-Hermitian Hamiltonian within the framework of the thermal diffusion equation, in which the interplay between intrinsic conduction, advection, and inflow can give rise to an exceptional point. The team experimentally studied the concomitant thermal transport by measuring the temperature distribution of the system under various conditions.
Intuitively, the thermal propagation appears to align with the advective flows induced by the two spinning plates. However, the team observed a directional dependence in the thermal transport that results from the nontrivial combination of the thermal inflow and the two imbalanced advective flows. Chirality is a hallmark of non-Hermitian systems [11], and the present experimental work demonstrated that non-Hermiticity yields chirality even for heat transport governed by the diffusion equation. Although this chiral heat transport was observed exclusively in the vicinity of the exceptional point, it was suppressed precisely at the exceptional point, implying a new underlying mechanism.
Chirality finds practical relevance in facilitating efficient transport of electricity, heat, and other quantities. Recent prime examples include topological materials, which exhibit chiral boundary states that are immune to imperfection and inhomogeneity. By contrast, the chiral heat transport realized by Qiu and colleagues relies on a different mechanism intrinsic to open systems, which may inspire new ideas for actively manipulating transport phenomena and for developing new devices.
Conventionally, dissipation has been considered as a nuisance that obscures interesting physics, compelling physicists to eliminate it from laboratory setups and practical applications. However, these two new experimental studies exemplify the utility of exceptional points in inherently dissipative systems. Further theoretical and experimental progress may lead to new physics in open systems that has no parallels in closed systems.
References
- R. El-Ganainy et al., “Non-Hermitian physics and PT symmetry,” Nat. Phys. 14, 11 (2018).
- C. Liang et al., “Observation of exceptional points in thermal atomic ensembles,” Phys. Rev. Lett. 130, 263601 (2023).
- G. Xu et al., “Non-Hermitian chiral heat transport,” Phys. Rev. Lett. 130, 266303 (2023).
- M.V. Berry, “Physics of nonhermitian degeneracies,” Czech. J. Phys. 54, 1039 (2004).
- C. M. Bender and S. Boettcher, “Real spectra in non-Hermitian Hamiltonians having symmetry,” Phys. Rev. Lett. 80, 5243 (1998).
- C. N. Yang and T. D. Lee, “Statistical theory of equations of state and phase transitions. I. Theory of condensation,” Phys. Rev. 87, 404 (1952); T. D. Lee and C. N. Yang, “Statistical theory of equations of state and phase transitions. II. Lattice gas and Ising model,” 87, 410 (1952).
- J. Wiersig, “Enhancing the sensitivity of frequency and energy splitting detection by using exceptional points: Application to microcavity sensors for single-particle detection,” Phys. Rev. Lett. 112, 203901 (2014).
- H. Hodaei et al., “Enhanced sensitivity at higher-order exceptional points,” Nature 548, 187 (2017); W. Chen et al., “Exceptional points enhance sensing in an optical microcavity,” 548, 192 (2017).
- P. Peng et al., “Anti-parity–time symmetry with flying atoms,” Nat. Phys. 12, 1139 (2016); Z. Zhang et al., “Observation of parity-time symmetry in optically induced atomic lattices,” Phys. Rev. Lett. 117, 123601 (2016).
- H.-K. Lau and A. A. Clerk, “Fundamental limits and non-reciprocal approaches in non-Hermitian quantum sensing,” Nat. Commun. 9, 4320 (2018); M. Zhang et al., “Quantum noise theory of exceptional point amplifying sensors,” Phys. Rev. Lett. 123, 180501 (2019).
- A. Regensburger et al., “Parity–time synthetic photonic lattices,” Nature 488, 167 (2012); L. Feng et al., “Experimental demonstration of a unidirectional reflectionless parity-time metamaterial at optical frequencies,” Nat. Mater. 12, 108 (2012); B. Peng et al., “Parity–time-symmetric whispering-gallery microcavities,” Nat. Phys. 10, 394 (2014).