Performance Capacity of a Complex Neural Network
Every day, our brain recognizes and discriminates the many thousands of sensory signals that it encounters. Today’s best artificial intelligence models—many of which are inspired by neural circuits in the brain—have similar abilities. For example, the so-called deep convolutional neural networks used for object recognition and classification are inspired by the layered structure of the visual cortex. However, scientists have yet to develop a full mathematical understanding of how biological or artificial intelligence systems achieve this recognition ability. Now SueYeon Chung of the Flatiron Institute in New York and her colleagues have developed a more detailed description of the connection of the geometric representation of objects in biological and artificial neural networks to the performance of the networks on classification tasks [1] (Fig. 1). The researchers show that their theory can accurately estimate the performance capacity of an arbitrarily complex neural network, a problem that other methods have struggled to solve.
Neural networks provide coarse-grained descriptions of the complex circuits of biological neurons in the brain. They consist of highly simplified neurons that signal one another via synapses—connections between pairs of neurons. The strengths of the synaptic connections change when a network is trained to perform a particular task.
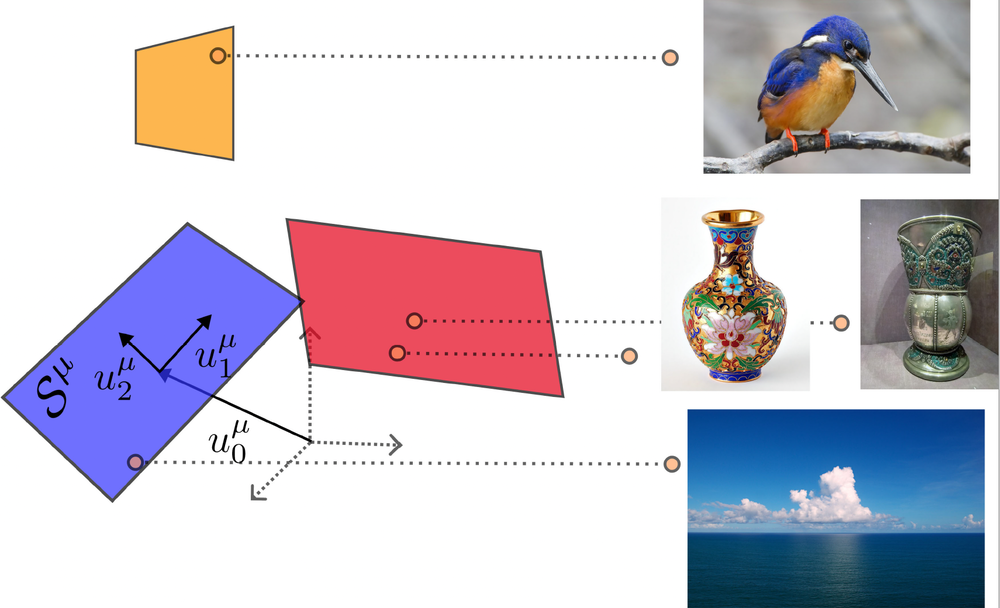
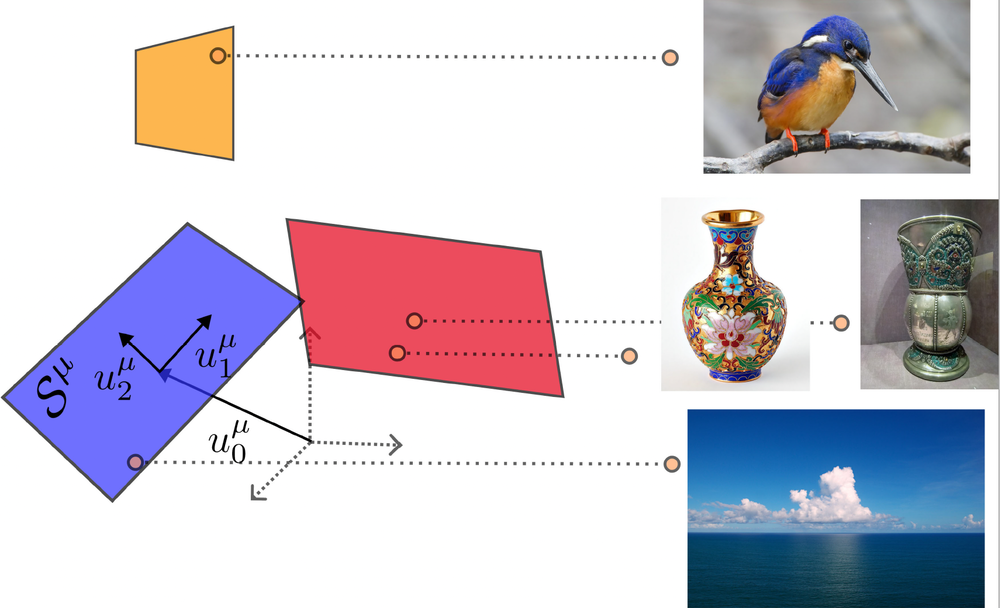
During each stage of a task, groups of neurons receive input from many other neurons in the network and fire when their activity exceeds a given threshold. This firing produces an activity pattern, which can be represented as a point in a high-dimensional state space in which each neuron corresponds to a different dimension. A collection of activity patterns corresponding to a specific input form a “manifold” representation in that state space. The geometric properties of manifold representations in neural networks depend on the distribution of information in the network, and the evolution of the manifold representations during a task is shaped via the algorithms training the network to perform the specific task.
The geometries of a network’s manifolds also constrain the network’s capacity to perform tasks, such as invariant object recognition—the ability of a network to accurately recognize objects regardless of variations in their appearance, including size, position, or background (Fig. 2). In a previous attempt to understand these constraints, Chung and a different group of colleagues studied simple binary classification tasks, ones where the network must sort stimuli into two groups based on some classification rule [2]. In such tasks, the capacity of a network is defined as the number of objects that it can correctly classify if the objects are randomly assigned categorizing labels.
For networks where each object corresponds to a single point in state space, a single-layered network with N neurons can classify 2N objects before the classification error becomes equivalent to that of random guessing. The formalism developed by Chung and her colleagues allowed them to study the performance of complex deep (multilayered) neural networks trained for object classification. Constructing the manifold representations from the images used to train such a network, they found that the mean radius and number of dimensions of the manifolds estimated from the data sharply decreased in deeper layers of the network with respect to shallower layers. This decrease was accompanied by an increased classification capacity of the system [2–4].
This earlier study and others, however, did not consider correlations between different object representations when calculating network capacity. It is well known that object representations in biological and artificial neural networks exhibit intricate correlations, which arise from structural features in the underlying data. These correlations can have important consequences for many tasks, including classification, because they are reflected in different levels of similarity between so-called pairs of classes in neural space. For example, in a network tasked with classifying whether an animal was a mammal, the dog and wolf manifold representations will be more similar than those of an eagle and a falcon.
Now Chung’s group has generalized their performance-capacity computation of deep neural networks to include correlations between object classes [1]. The team derived a set of self-consistent equations that can be solved to give the network capacity for a system with homogeneous correlations between the so-called axes (the dimensions along which the manifold varies) and centroids (the centers of manifolds) of different manifolds. The researchers show that axis correlations between manifolds increase performance capacity, whereas centroid correlations push the manifolds closer to the origin of the neural state space, decreasing performance capacity.
Over the past few years, the study of neural networks has seen many interesting developments, and more data-analysis tools are increasingly being developed to better characterize the geometry of the representations obtained from neural data. The new results make a substantial contribution in this area, as they can be used to study the properties of learned representations in networks trained to perform a large variety of tasks in which correlations present in the input data may play a crucial role in learning and performance. These tasks include those related to motor coordination, natural language, and probing the relational structure of abstract knowledge.
References
- A. J. Wakhloo et al., “Linear classification of neural manifolds with correlated variability,” Phys. Rev. Lett. 131, 027301 (2023).
- S. Y. Chung et al., “Classification and geometry of general perceptual manifolds,” Phys. Rev. X 8, 031003 (2018).
- E. Gardner, “The space of interactions in neural network models,” J. Phys. A: Math. Gen. 21, 257 (1988).
- U. Cohen et al., “Separability and geometry of object manifolds in deep neural networks,” Nat. Commun. (2019).