The Cost of Sending a Bit Across a Living Cell
For a cell to stay alive, its different parts must be able to exchange signals. Transmitting signals consumes energy, of which every cell has a limited supply. Now Samuel Bryant and Benjamin Machta, two physicists at Yale University, have derived the minimum energy that a cell needs to transmit an internal signal using electrical current, molecular diffusion, or sound waves [1]. Their calculations show that the most efficient signaling mechanism depends on several factors, including the distance that the signal needs to travel. This finding matches everyday human experiences of communication: sound waves suffice if we are talking to someone in the same room, but electromagnetic waves are needed for continent-spanning discussions.
From an energy perspective, a living organism is a nonequilibrium system whose existence depends on ongoing exchanges of energy with its environment. As such, living organisms can be compared to certain nonliving nonequilibrium systems, including hurricanes and fires. But, unlike those nonliving systems, living organisms must also send and receive information in order to survive. That information may be about their internal state or their external environment. Thus, we can think of the presence of intertwined energy and information flows as being a defining signature of living matter. The study performed by Bryant and Machta explores—at the fundamental level—this energy–information relationship in molecular systems.
Researchers have traditionally used one of two approaches to study the connection between energy and information in biology. The first approach—which for ease of explanation I will term the first-principles approach—has at its foundation the first and second laws of thermodynamics, which state that the total energy of a system is conserved over time and that its entropy always increases. The first-principles approach has been used to understand the energy requirements for copying and sensing in molecular systems [2, 3], as well as other information-processing tasks. The approach involves only a few assumptions, so results derived from it tend to be quite general. However, it does not factor in many of the specific physical and evolutionary constraints faced by organisms, such as that cells are composed of soft matter and exposed to significant thermal noise and mechanical perturbation. For this reason, energetic bounds calculated using this approach can significantly underestimate the actual amount of energy that cells need to carry out certain functions [4].
The second approach—which I will term the model-based approach—starts with an existing empirical model for the system under consideration, into which researchers may input experimental data. For example, a model-based study of the energetic costs of gene expression and their evolutionary consequences might use measured values of the consumption of the energy-carrying molecule ATP (adenosine triphosphate) involved in transcription and translation, two processes required for gene expression [5]. Results derived from the model-based approach tend to be less generalizable than those derived from first principles. But they are typically more accurate, since they account for the constraints of real biological systems. As such, this approach is used more often by biological physicists and theoretical biologists.
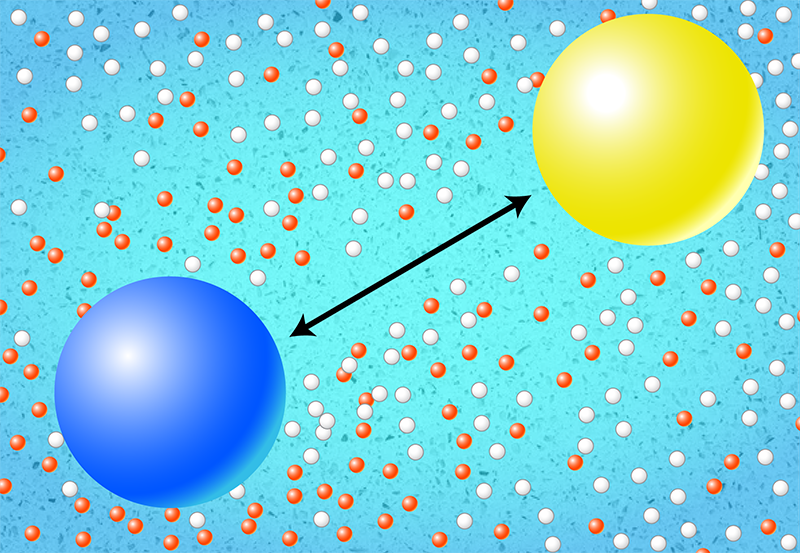
While researchers studying energy–information relationships in biological systems commonly use the first-principles approach, Bryant and Machta adopt the model-based approach to understand the energetic costs of cell signaling. They developed three different models, each involving a different signaling method: electrical current, molecular diffusion (both in two and three spatial dimensions), or sound waves. The models account for the physical principles underlying the mechanisms that a cell can use to send and receive information. For example, for transmission using electrical currents, the sender controls the amount of current flowing through a membrane-bound ion channel, which then affects the electrical charge at a receiver located somewhere else on the membrane. For the molecular-diffusion model, the sender controls the local concentration of the messenger molecules, which then diffuse to the receiver (Fig. 1). Finally, for the sound-wave model, the sender generates the signal-carrying compression waves, which then propagate through the cell’s innards to the receiver.
By making some elegant simplifying approximations, and by treating the sender’s signal as a mixture of oscillating waves, Bryant and Machta derived a formula for the minimum energetic cost to send a bit of information for each model. The energy-cost equations are expressed in terms of bits and each include four key parameters—the transmission distance, the oscillation frequency of the sender’s signal, and the physical sizes of the sender and the receiver.
These equations show that each mechanism has an optimal signal frequency and a characteristic spatial scale that marks the distance beyond which the energetic cost of sending a bit becomes prohibitive. For diffusion in three dimensions, the optimal frequency is low and the maximum distance small. For instance, the energetic cost of transmitting a 1-kHz signal becomes prohibitive for distances above 1 µm, the typical size of a prokaryotic cell. For sound, the frequency is high and the maximum distance large, acoustic transmission at 1 kHz remaining energetically viable for distances of up to 1 cm.
While the study provides clear predictions, these results mark the beginning of this scientific story, not the end. For instance, the theoretical predictions have not yet been compared to data from real-world organisms. That step is needed so that researchers can quantify the efficiency of actual biological signaling systems and then investigate whether biology has evolved optimized signaling mechanisms. Also, Bryant and Machta do not consider “active” signaling processes that occur in excitable biological systems, such as neurons in the brain or the membranes of developing egg cells [6]. Nonetheless, this study provides a promising route for exploring the efficiency of a wide range of biological signaling systems—an exploration needed if scientists are to fully understand how energy and information come together to produce living matter.
References
- S. J. Bryant and B. B. Machta, “Physical constraints in intracellular signaling: The cost of sending a bit,” Phys. Rev. Lett. 131, 068401 (2023).
- D. Andrieux and P. Gaspard, “Nonequilibrium generation of information in copolymerization processes,” Proc. Natl. Acad. Sci. U.S.A. 105, 9516 (2008).
- A. C. Barato et al., “Efficiency of cellular information processing,” New J. Phys. 16, 103024 (2014).
- S. B. Laughlin et al., “The metabolic cost of neural information,” Nat. Neurosci. 1, 36 (1998).
- A. Wagner, “Energy constraints on the evolution of gene expression,” Mol. Biol. Evol. 22, 1365 (2005).
- T. H. Tan et al., “Topological turbulence in the membrane of a living cell,” Nat. Phys. 16, 657 (2020).