Toward a Complete Theory of Crystal Vibrations
Although a crystal is a highly ordered structure, it is never at rest: its atoms are constantly vibrating about their equilibrium positions—even down to zero temperature. Such vibrations are called phonons, and their interaction with the electrons that hold the crystal together is partly responsible for the crystal’s optical properties, its ability to conduct heat or electricity, and even its vanishing electrical resistance if it is superconducting. Predicting, or at least understanding, such properties requires an accurate description of the interplay of electrons and phonons. This task is formidable given that the electronic problem alone—assuming that the atomic nuclei stand still—is already challenging and lacks an exact solution. Now, based on a long series of earlier milestones, Gianluca Stefanucci of the Tor Vergata University of Rome and colleagues have made an important step toward a complete theory of electrons and phonons [1].
At a low level of theory, the electron–phonon problem is easily formulated. First, one considers an arrangement of massive point charges representing electrons and atomic nuclei. Second, one lets these charges evolve under Coulomb’s law and the Schrödinger equation, possibly introducing some perturbation from time to time. The mathematical representation of the energy of such a system, consisting of kinetic and interaction terms, is the system’s Hamiltonian. However, knowing the exact theory is not enough because the corresponding equations are only formally simple. In practice, they are far too complex—not least owing to the huge number of particles involved—so that approximations are needed. Hence, at a high level, a workable theory should provide the means to make reasonable approximations yielding equations that can be solved on today’s computers.
One way to reduce the complexity of the problem is to step back from the picture of individual particles in favor of one of effective quasiparticles specific to the system at hand. An early example of a quasiparticle in the literature is the phonon: instead of focusing on the atomic nuclei that could, in principle, be located anywhere in space, one considers their collective vibration about their positions in a predefined crystal structure. Scientists have studied such “elastic waves” for almost a century [2], often resorting to two famous approximations: the Born-Oppenheimer approximation, which assumes that the electrons respond instantaneously to displacements of the nuclei; and the harmonic approximation, which posits that this response results in restoring forces proportional to the displacements.
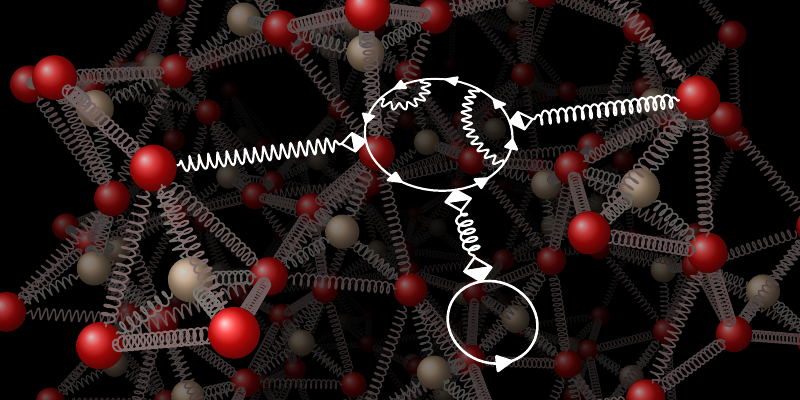
Stefanucci and colleagues’ work builds on studies made in the middle of the last century that analyzed the interaction between quasiparticles by borrowing tools from quantum field theory. In 1961, Gordon Baym published a corresponding theory of electrons and phonons, in which the phonon field assigns a displacement to points in space and time [3]. One of the aforementioned tools is the technique of Feynman diagrams, which represent interaction processes graphically (Fig. 1) and can be translated into mathematical formulas through simple rules. By combining such diagrams into sets of equations that recursively depend on each other, one can account for all possible processes occurring in physical reality. In 1965, Lars Hedin presented examples of such equations, which completely describe systems of interacting electrons [4]. In a 2017 review, Feliciano Giustino merged these approaches and coined the term Hedin-Baym equations in the context of state-of-the-art materials simulations—answering many, but not all, open questions [5].
Stefanucci and colleagues have addressed several of the remaining issues [1]. First, they imposed requirements on the electron–phonon Hamiltonian, avoiding the mistake of trying to solve a problem not properly formulated in the first place. They emphasized that the equilibrium state around which the theory is built is not known in advance, making setting up and evaluating the Hamiltonian an iterative procedure. They also stressed that this Hamiltonian cannot generally be written in terms of physical phonons, contrary to what is often supposed. Second, the team generalized Giustino’s work [5] to systems driven out of equilibrium at any temperature—a key advance because this scenario reflects experimental and technological conditions. Mathematically, this generalization allows time to take on complex values. Third, the researchers carefully derived the corresponding rules for Feynman diagrams and provided the first complete set of diagrammatic Hedin-Baym equations. Such equations form the basis of systematic approximations, in which certain diagrams are neglected, and provide a criterion [3] for the resulting dynamics to respect fundamental conservation laws. Whereas the effects of electrons on phonons and vice versa are well studied separately [5], here it is crucial that both occur simultaneously.
Nowadays, parameter-free simulations of electrons and phonons rely heavily on so-called density-functional perturbation theory [6], which is based on the Born-Oppenheimer and harmonic approximations. By contrast, diagrammatic techniques are often—but not always [7]—used in combination with parameterized model Hamiltonians. Efforts to bring both approaches together have led to so-called downfolding methods, which already exist for the electron–phonon problem [8]. The insights gained by Stefanucci and colleagues will certainly help to further bridge the different strategies. Moreover, the advancements beyond thermal equilibrium will be of utmost importance because such an extension is needed to explain the latest time-resolved spectroscopy experiments and to design better photovoltaics. Finally, given that the team’s results apply to any fermion–boson system, such as an interacting light–matter system, many fields will benefit from this seminal work.
References
- G. Stefanucci et al., “In and out-of-equilibrium ab initio theory of electrons and phonons,” Phys. Rev. X 13, 031026 (2023).
- F. Bloch, “On the quantum mechanics of electrons in crystal lattices,” Z. Phys. 52, 555 (1929).
- G. Baym, “Field-theoretic approach to the properties of the solid state,” Ann. Phys. 14, 1 (1961).
- L. Hedin, “New method for calculating the one-particle Green’s function with application to the electron-gas problem,” Phys. Rev. 139, A796 (1965).
- F. Giustino, “Electron-phonon interactions from first principles,” Rev. Mod. Phys. 89, 015003 (2017).
- S. Baroni et al., “Phonons and related crystal properties from density-functional perturbation theory,” Rev. Mod. Phys. 73, 515 (2001).
- A. Marini et al., “Many-body perturbation theory approach to the electron-phonon interaction with density-functional theory as a starting point,” Phys. Rev. B 91, 224310 (2015).
- Y. Nomura and R. Arita, “Ab initio downfolding for electron-phonon-coupled systems: Constrained density-functional perturbation theory,” Phys. Rev. B 92, 245108 (2015).