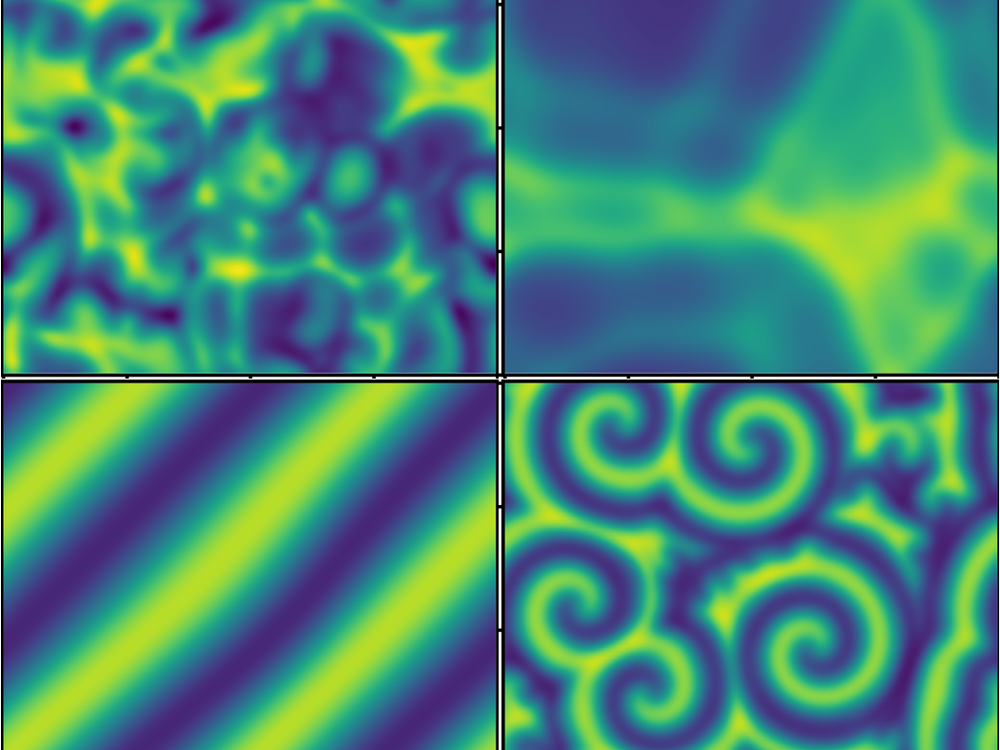
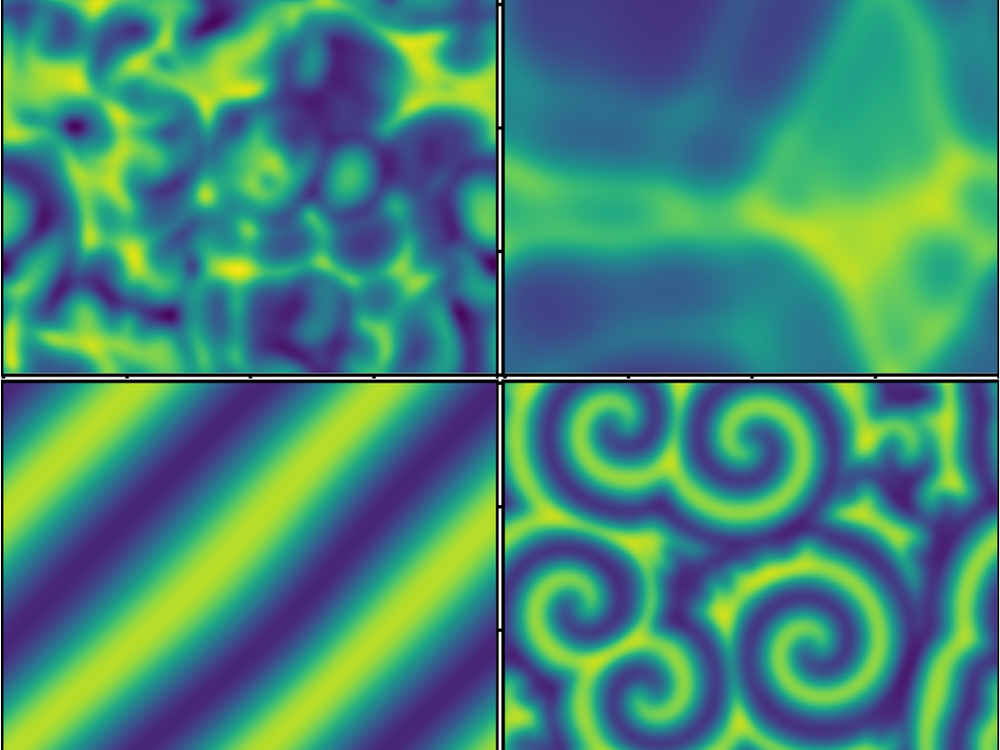
Learning Governing Equations and Control Parameters from Data
With the advent of machine-learning algorithms came the dream of quick-and-easy scientific discoveries, where an algorithm crunches observational data and then spits out a model that describes how the measured system behaves. Back in 2016, a team of researchers at the University of Washington, Seattle, took a step toward that dream, creating a robust model-generating algorithm that used measurements of a pattern-forming system to determine that system’s governing equations [1]. Now the same team has improved that algorithm so that, as well as predicting a system’s governing equations, it can identify a system’s key behavior-controlling parameters [2]. J. Nathan Kutz, who headed the study, says that this advance makes the algorithm useful for gleaning information about real systems for which the control parameters are unknown. The algorithm could also be used to predict the behavior of a system under conditions for which there are currently no data.
Imagine walking from your kitchen to your sofa with a steaming mug of hot coffee. Walk slowly, and the liquid will likely stay in the mug, even while its surface rocks gently back and forth. Walk quickly, however, and the liquid may splash out of the mug—and possibly onto your clothes—as the waves become too high for the mug to contain. There are many parameters—from how much coffee is in the cup to the speed you walk—that go into understanding whether the coffee stays in the mug or breaches its banks. The machine-learning algorithm developed by Kutz and his team can take the data points of the coffee’s top surface over time and then infer which of these parameters are the key ones for predicting how the coffee behaves.
The researchers demonstrated their method by first generating two libraries of parameters. One library contained the hundreds of terms that might turn up in an equation describing a system’s behavior, the other a list of all the possible control parameters. They then input both libraries and a set of data into the algorithm. The algorithm filtered the library terms, using a particular implementation technique known as sparse matrix regression, until it had the minimal number of terms it needed to correctly describe the data and the factors that controlled the data.
The researchers tested their model on a hypothetical system governed by the Ginzburg-Landau equation, a mathematical construction used, for example, to describe superconductor phase transitions. They also demonstrated it on a model chemical system containing components that oscillate in concentration. “We put all the known physics into a library, and the algorithm picked out only the bits it needed to describe the systems,” Kutz says. “That’s the whole trick to this method.”
The 2016 algorithm worked in a similar way, but it used only one library—that of the governing-equation parameters. Also, when the 2016 algorithm was presented with a calmly rocking coffee surface and a chaotically splashing one, it could spit out different sets of governing equations. The update removes that problem by adding in a training step that aids the algorithm in recognizing when two datasets come from measurements of one system. The update also allows the algorithm to infer critical values for control parameters, such as the fastest speed you can walk without your coffee spilling.
Despite the various improvements, Kutz notes that the accuracy of their algorithm-determined governing equations can—like those predicted using other methods—depend on the level of noise in the measurements. The new algorithm does include a noise-mitigation strategy, which was developed by a team led by David Bortz, an applied mathematician at the University of Colorado Boulder [3]. However, if the noise goes above some threshold, the algorithm can produce an ill-fitted model.
Nevertheless, Bortz says that the approach of Kutz and his colleagues could be useful in understanding any system for which there is a lot of data but no way of gleaning the behavior from first principles. “The use cases are ubiquitous,” he says. Kutz is particularly excited about applying the technique to understanding turbulence and to modeling the behavior of neurons in the brain, two systems for which scientists are struggling to build reliable mathematical models. In outputting equations akin to the ones traditionally created by physicists, Kutz says that his team’s algorithm stands out among machine-learning algorithms, which tend to act like black boxes and spit out results that are difficult to interpret.
Correction (6 November 2023): In a previous version of the story, Bortz was identified as a computer scientist. He is an applied mathematician.
Correction (29 November 2023): A previous version of this story implied that Kutz and his colleagues came up with the idea of sparse optimization for learning equations from data. That idea was originally proposed in 2011 by another group.
–Dina Genkina
Dina Genkina is a freelance science writer and a science communicator at the Joint Quantum Institute, Maryland. She works in Brooklyn, New York.
References
- S. L. Brunton et al., “Discovering governing equations from data by sparse identification of nonlinear dynamical systems,” Proc. Natl. Acad. Sci. U.S.A. 113, 3932 (2016).
- Z. G. Nicolaou et al., “Data-driven discovery and extrapolation of parameterized pattern-forming dynamics,” Phys. Rev. Research 5, L042017 (2023).
- D. A. Messenger and D. M. Bortz, “Weak SINDy for partial differential equations,” J. Comput. Phys. 443, 110525 (2021).