Decoding the Dynamics of Supply and Demand
Understanding why prices change is one of the most important and fascinating problems in economics. The law of supply and demand posits that an increase in supply lowers prices, while an increase in demand raises them, yet the intricate inner workings of this mechanism remain partially obscured. Despite the many theoretical frameworks proposed, a rigorous scientific approach mandates that conclusive answers be grounded in empirical evidence. Thanks to their extensive digitalization, financial markets provide an unparalleled wealth of data in terms of quantity, quality, and level of detail. Now Yuki Sato and Kiyoshi Kanazawa at Kyoto University in Japan have used this data-rich environment to test a key economic theory with unprecedented precision [1, 2]. The team’s results shed light on how long-range correlations in financial markets emerge from small-scale dynamics.
In 2004, J. Doyne Farmer and I reported strong temporal correlations in the sequence of buyer- and seller-initiated trades [3]. More precisely, by denoting a buyer-initiated trade with +1 and a seller-initiated trade with –1, the researchers found that the autocorrelation function of this binary sequence—a measure of how similar the sequence is at different times—exhibits a remarkably slow decay. The function approaches zero according to a power-law function with an exponent 𝛾 less than 1. This empirical finding is consistent with a process displaying long-range correlations, also known as a long-memory process [4]. Such processes manifest in many physical, biological, and social systems, and they are widely explored in the physics literature because of their connection to anomalous diffusion [5]. The remarkable observation of long memory in market trading, subsequently confirmed for various markets, assets, and time periods, underlines the significant temporal autocorrelation in supply-and-demand dynamics.
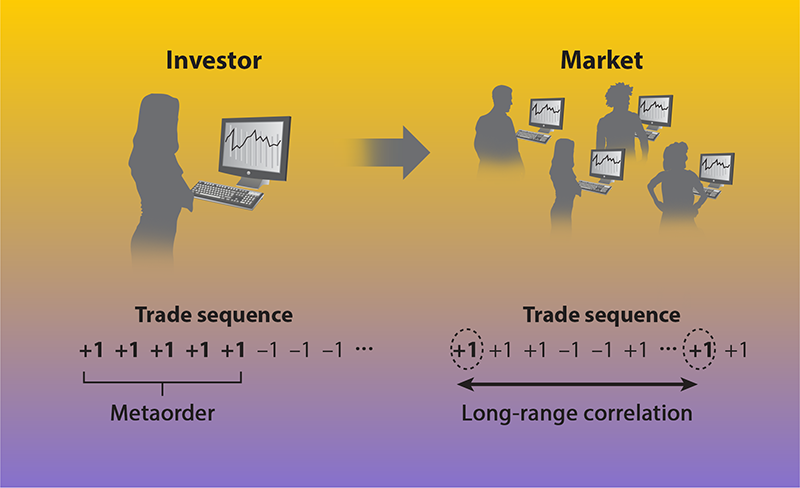
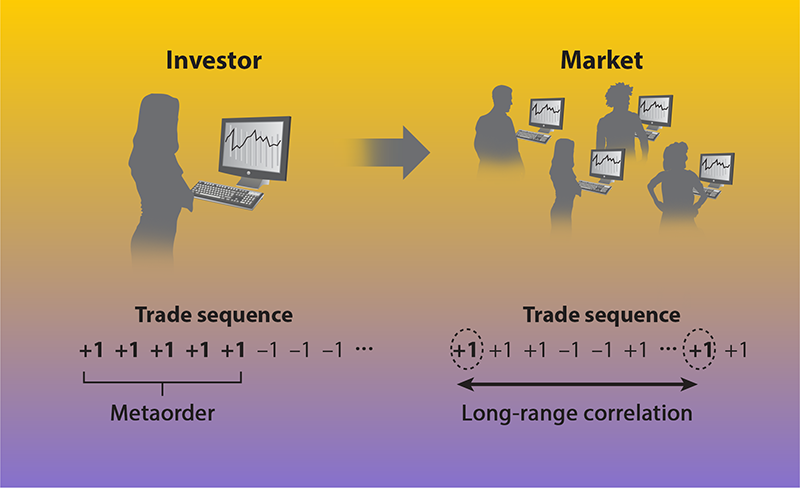
Uncertainty over the origin of this intriguing empirical phenomenon has spurred extensive research. In 2005, Szabolcs Mike, Farmer, and I proposed a simple model in which medium and large investors, such as banks, funds, and insurance companies, are unable to execute a large order owing to the low available liquidity—the ability to exchange assets for money [6]. Consequently, these investors resort to trading their large orders, termed metaorders, incrementally over an extended period of time (Fig. 1).
The Lillo-Mike-Farmer (LMF) model provides a quantitative relationship between the autocorrelation function of buyer- and seller-initiated trades and the distribution of metaorder sizes. Notably, to reproduce the aforementioned long memory, the metaorder-size distribution must exhibit a power-law tail with an exponent 𝛼 equal to 𝛾+1 and therefore less than 2. This requirement signifies that the variance of metaorder sizes is infinite and that the distribution belongs to the Lévy domain—a mathematical domain that is heavily studied in the physics community. From an economics perspective, the LMF model indicates that markets are characterized by a huge heterogeneity in investor size, because the size of a metaorder is likely related to the size of the investor’s portfolio. The model also suggests that the long memory in supply and demand is related to this heterogeneity.
Careful testing of the LMF model poses a formidable challenge, primarily because the identification of metaorders remains elusive when using publicly available data. These datasets typically provide details about each trade—such as price, volume, and time—yet crucially lack any references to the investors behind those transactions.
Sato and Kanazawa gained access to a unique database of the Tokyo Stock Exchange that spans the years 2012–2020 and that contains the coded identities of the investors in each trade. Leveraging this privileged resource, the researchers devised an ingenious statistical approach to identify metaorders. Their methodology revolved around grouping trades involving the same asset, executed in the same direction (buy or sell), and undertaken by the same investor within a short time frame. The team investigated the distribution of metaorder sizes, finding a power-law tail with an exponent 𝛼 remarkably close to 3/2. This observation, robustly consistent across time and assets, underscores the pervasive presence of the substantial investor-size heterogeneity posited by the LMF model in financial markets.
More importantly, Sato and Kanazawa empirically tested the exponent relationship 𝛼=𝛾+1 predicted by the LMF model. By measuring the exponents 𝛼 and 𝛾 for each stock, the researchers found excellent agreement between theory and experiment. This compelling result provides strong evidence that the mechanism proposed by the LMF model effectively accounts for the remarkable long-lasting persistence of supply-and-demand dynamics in financial markets.
Contrary to standard economic theories, financial markets live in a state of latent supply and demand whose changes are very slowly made visible through trades. This hidden nature of supply and demand gives rise to extended correlations and memory in market dynamics—challenging the conventional wisdom that markets are always in a state of equilibrium between supply and demand. Intriguingly, this perspective has recently gained further support [7], proving highly effective in elucidating how prices respond to the arrival of substantial metaorders. Such clarification is of paramount importance both to understand how information is incorporated into prices and to quantify transaction costs.
Sato and Kanazawa’s investigation solves a long-standing problem in the study of financial markets and provides potentially useful hints for the modeling of other complex systems—such as DNA sequences, internet traffic, linguistics, and hydrological and geophysical processes. The work is also another clear demonstration that we have entered an era in which economic and financial data are of such quality that theoretical ideas and models can be tested with standards comparable to those of the physical sciences.
References
- Y. Sato and K. Kanazawa, “Inferring microscopic financial information from the long memory in market-order flow: A quantitative test of the Lillo-Mike-Farmer model,” Phys. Rev. Lett. 131, 197401 (2023).
- Y. Sato and K. Kanazawa, “Quantitative statistical analysis of order-splitting behavior of individual trading accounts in the Japanese stock market over nine years,” Phys. Rev. Research 5, 043131 (2023).
- F. Lillo and J. D. Farmer, “The long memory of the efficient market,” Stud. Nonlinear Dyn. Econ. 8, 1 (2004).
- J. Beran, Statistics for Long-Memory Processes, Monographs on Statistics and Applied Probability Vol. 61 (Chapman & Hall, Boca Raton, FL, 1994)[Amazon][WorldCat].
- J.-P. Bouchaud and A. Georges, “Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications,” Phys. Rep. 195, 127 (1990).
- F. Lillo et al., “Theory for long memory in supply and demand,” Phys. Rev. E 71, 066122 (2005).
- F. Bucci et al., “Crossover from linear to square-root market impact,” Phys. Rev. Lett. 122, 108302 (2019).