Quantum Fluids of Light Come into Sharper View
Superfluidity [1, 2], the ability of a fluid to flow without friction, isn’t restricted to systems described by hydrodynamics. Over a decade ago, optics researchers started to take an interest in superfluids and other quantum fluids [3], driven by the realization that light propagating in a nonlinear medium can exhibit quantum hydrodynamics features [4]. Two platforms emerged for the study of these “fluids of light”: semiconductor microcavities in which photons are confined [5] and propagating geometries in which photons travel in a bulk medium [6–8]. Both configurations allow photons to acquire an effective mass and experience an effective mutual interaction—properties that can lead them to collectively behave as a quantum fluid. Our understanding of these exotic states, however, is hampered by experimental limitations—in particular, the difficulty of probing the collective excitations that are hallmarks of quantum-fluid behavior. Now Ferdinand Claude of the Kastler-Brossel Laboratory (LKB) of Sorbonne University, France, and co-workers have provided an unprecedentedly detailed characterization of a quantum fluid of polaritons—quasiparticles resulting from the strong coupling of photons and excitons in a semiconductor microcavity [9]. Their approach holds promise for exploring new quantum-fluid regimes, including some that could serve as analog models of gravity.
Semiconductor microcavities offer a powerful platform to observe photon-hydrodynamical effects. When such a cavity is illuminated by electromagnetic waves whose frequency matches the cavity resonance, the component of the wave vector perpendicular to the plane of the cavity becomes quantized. As a result, the relation between this wave vector component and the photon frequency exhibits a quadratic dependence that confers an effective mass to the photons. Simultaneously, the laser illumination creates bound hole–electron states, called excitons. The coupling between photons and excitons in the cavity gives rise to quasiparticles called polaritons, which inherit the properties of both photons and excitons. These polaritons have a mass determined by the exciton effective mass and the photon effective mass and they interact via exciton–exciton coupling. They can thus behave collectively as a flow of massive, interacting particles—that is, as a quantum fluid. In the last decade, polaritonic systems have indeed been shown to display quantum-fluid behaviors ranging from Bose-Einstein condensation to superfluidity.
The similarity between cavity polaritons and two-dimensional quantum fluids goes beyond this qualitative description, as the time evolution of both systems is ruled by the same mathematical formalism: the so-called Gross-Pitaevskii equation. One hallmark of quantum-fluid behavior is the existence of collective excitations—in particular, small density perturbations that propagate on the surface of the fluid at rest. This propagation is described by a Bogoliubov-like dispersion relation, one that has a sound-like region (a linear energy-momentum relation on large length scales) and a free-particle-like region (a parabolic relation on small length scales). Claude and co-workers focus on the quantitative measurement of these collective excitations, also known as Bogoliubov waves.
Unlike propagating geometries, cavity-polariton systems require extensions of the Bogoliubov theory—a consequence of the out-of-equilibrium nature of polaritons, which are generated via laser photoexcitation and have a finite lifetime. This difference implies challenges in the acquisition and exploitation of experimental data. Measurements of the Bogoliubov excitations involve exciting polaritons using a “pump” laser and then detecting the photoluminescence generated when the polaritons decay. In earlier studies, the pump laser frequency was far from the cavity resonance—which facilitates the separation of pump photons from the photoluminescence photons. The nonresonant excitation, however, produces a broad range of polaritons, some of which aren’t part of the quantum fluid. Their presence distorts the measured spectra, especially in those regions (low wave numbers) where the signatures of superfluidity are expected. An alternative approach is to illuminate the cavity with a near- or on-resonance pump (which has to be filtered out from the photoluminescence photons). This approach, however, doesn’t have sufficient energy resolution to observe many subtle features of the Bogoliubov dispersion curve.
Thanks to an innovative technique based on coherent-probe spectroscopy, which the group previously developed [10], the researchers were able to overcome these limitations. In the technique, the pump pulse is followed by a tunable laser field that probes the Bogoliubov excitations. The probe laser allows the signal to be isolated from the background emission from the fluid, giving the setup an ability to access features of the polaritonic fluid with unprecedented spatial and spectral resolution.
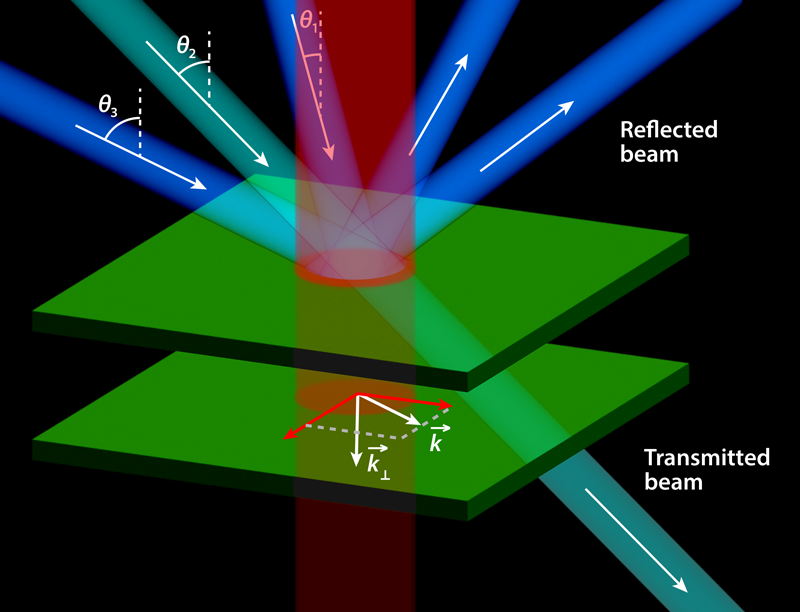
Through a series of experiments, Claude and co-workers delivered a comprehensive characterization of the dispersion of collective excitations of the polaritonic fluid. For a given pump energy, they measured, for different angles of the probe beams, the reflectivity of the cavity (Fig. 1) . For each angle, the reflectivity displayed a dip when the probe was resonant with collective polariton excitations, which allowed the researchers to characterize Bogoliubov excitations with different wave vectors and thus to reconstruct the dispersion relation. Moreover, they exploited the beams’ Gaussian shape to fit their experimental results to theoretical predictions that accounted for such shapes—a procedure that allowed them to extract the speed of sound in the polaritonic fluid.
In a superfluid, the Bogoliubov dispersion relation has two branches, one with normal dispersion and one with negative dispersion, also known as the ghost branch. The latter branch owes its name to the fact that it is very challenging to excite—and thus to observe. The exquisite sensitivity of the pump-probe setup has previously allowed the LKB researchers to overcome this experimental difficulty and find traces of this ghost branch in reflectivity measures of their cavity [10]. The new work provides a remarkable improvement in the characterization of both branches, in particular, for regions of the dispersion curves that were poorly characterized until now—such as those corresponding to low wave numbers. The team was also able to observe new details of how fluid density and other parameters affect the speed of sound and to characterize the onset of various fluid instabilities.
The framework of quantum fluids gains, thanks to this study, a level of experimental control that paves the way to even more extensive quantitative studies of polaritonic fluids. By probing tiny deviations from standard quantum-fluid behavior, the setup will enable unprecedented insights into quantum hydrodynamics. What’s more, it might enable the use of polaritonic systems as optical analogs of gravity, which could be used to simulate hard-to-probe phenomena relevant to astrophysics, cosmology, and quantum gravity.
References
- P. Kapitza, “Viscosity of liquid helium below the 𝜆-point,” Nature 141, 74 (1938).
- J. F. Allen and A. D. Misener, “Flow of liquid helium II,” Nature 141, 75 (1938).
- A. Amo et al., “Superfluidity of polaritons in semiconductor microcavities,” Nat. Phys. 5, 805 (2009).
- T. Frisch et al., “Transition to dissipation in a model of superflow,” Phys. Rev. Lett. 69, 1644 (1992).
- I. Carusotto and C. Ciuti, “Quantum fluids of light,” Rev. Mod. Phys. 85, 299 (2013).
- I. Carusotto, “Superfluid light in bulk nonlinear media,” Proc. R. Soc. A. 470, 20140320 (2014).
- Q. Fontaine et al., “Observation of the Bogoliubov dispersion in a fluid of light,” Phys. Rev. Lett. 121, 183604 (2018).
- C. Michel et al., “Superfluid motion and drag-force cancellation in a fluid of light,” Nat. Commun. 9, 2108 (2018).
- F. Claude et al., “Spectrum of collective excitations of a quantum fluid of polaritons,” Phys. Rev. B 107, 174507 (2023).
- F. Claude et al., “High-resolution coherent probe spectroscopy of a polariton quantum fluid,” Phys. Rev. Lett. 129, 103601 (2022).