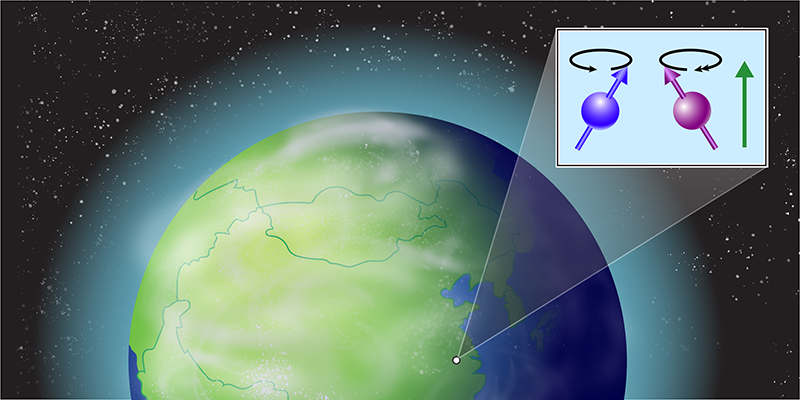
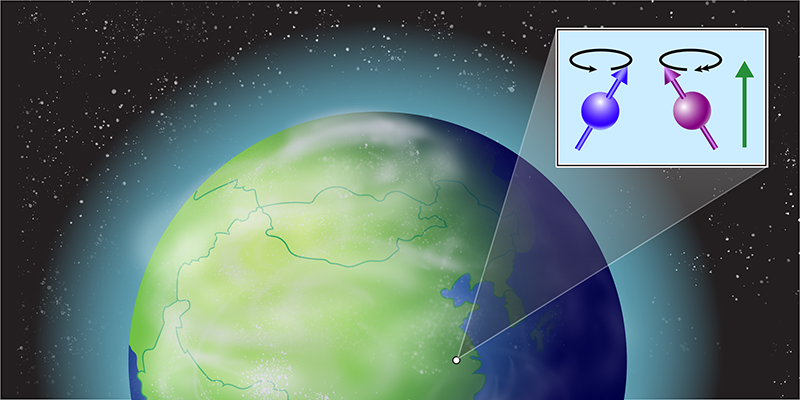
Testing Gravity’s Effect on Quantum Spins
Our understanding of physics is supported by two theoretical pillars. The first is quantum field theory, which underpins the standard model of particle physics. And the second is Einstein’s theory of general relativity, which describes the nature of gravity. Both pillars have withstood numerous stringent tests and have had myriad predictions spectacularly confirmed. Yet they are seemingly irreconcilable, hinting at a deeper truth. The path toward reconciling these theories is obscured by the dearth of experiments probing phenomena at the intersection of quantum physics and gravity. Now a team of researchers from the University of Science and Technology of China (USTC), led by Dong Sheng and Zheng-Tian Lu, has stepped into this breach by searching for an interaction between a particle’s intrinsic quantum spin and Earth’s gravitational field with unprecedented sensitivity (Fig. 1) [1]. Although no evidence for this interaction was found, the search yielded strong constraints that have implications for the existence of hypothetical forces of nature and for the origin of the matter–antimatter asymmetry of the Universe.
Intrinsic spin is a purely quantum form of angular momentum whose essence does not involve the physical rotation of a particle; its explanation emerges from Dirac’s unification of quantum mechanics and special relativity [2]. By contrast, gravitational fields are understood through general relativity: a classical theory that describes angular momentum arising only from the rotation of large, massive bodies. So how does a quantum spin interact with a gravitational field? That question remains open.
The USTC team developed an exquisitely accurate experiment to test whether the energy associated with the spin of an atomic nucleus depends on the spin’s orientation relative to Earth’s gravitational field. Consider the analogous case of a nuclear spin in a magnetic field: the spin’s energy depends on its orientation relative to the field because of its magnetic moment. This phenomenon, known as the Zeeman effect, is the basis for nuclear magnetic resonance (NMR) and magnetic resonance imaging (MRI). It causes spins tilted from the magnetic-field axis to precess—wobble like a spinning top—at a characteristic frequency called the Larmor frequency. Similarly, if a spin–gravity interaction existed, spins would precess in a gravitational field [3].
If gravity coupled directly to spin with the same strength that it couples to mass, spins would precess at a frequency of about 10 nHz in Earth’s gravitational field. That value is more than 10 billion times smaller than the typical nuclear Larmor frequency in Earth’s magnetic field and is roughly a thousandth of our planet’s rotation rate of once per day. These comparisons illustrate the daunting challenges the USTC team faced. In particular, systematic errors caused by magnetic fields and by gyroscopic effects associated with Earth’s rotation needed to be understood and controlled at extraordinary levels to detect a possible spin–gravity interaction.
The USTC team’s approach involved a spin-polarized gas composed of two different isotopes: xenon-129 and xenon-131. The researchers simultaneously measured the nuclear-spin precession frequencies of the two isotopes in an applied magnetic field. The direction of this field was carefully aligned parallel to Earth’s rotation axis to minimize the systematic errors caused by gyroscopic effects. By taking the ratio of the two precession frequencies, the team precisely canceled magnetic-field-dependent effects. This frequency ratio was repeatedly measured as the direction of the magnetic field was reversed, and the difference between the ratios corresponding to the two different field directions was determined. To first order, this difference is proportional to the magnitude of precession caused by nonmagnetic effects, such as that arising from gravity-induced torque on spins. The researchers’ thorough analysis of the data revealed no evidence of a spin–gravity interaction.
Given the structure of the xenon-129 and xenon-131 nuclei, the USTC experiment is mainly sensitive to the strength with which gravity couples to neutron spins. The team’s measurements establish the most stringent constraint on any coupling of intrinsic spin to gravity. The derived limit for neutrons shrinks previous bounds by a factor of 17, and it surpasses constraints for electrons by 400 and those for protons by 6000 [1]. For comparison, the experiment is sensitive to spin precession frequencies more than a hundred times smaller than Earth’s rotation rate.
The manifestation of the spin–gravity interaction sought in the USTC experiment is indistinguishable from a long-range force mediated by an exotic boson such as the axion [4]. The axion is a hypothetical particle predicted by many theoretical extensions to the standard model and is a promising candidate to explain dark matter [5]. The USTC measurements far surpass previous limits on the strength of particular axion-mediated forces, even the severe bounds derived from astrophysical observations.
Of particular interest is the fact that the USTC experiment probes a spin–gravity interaction that violates the fundamental symmetries of parity (P), corresponding to symmetry upon the reflection of coordinate axes through the origin, and time reversal (T) [6]. Quantum field theory predicts that interactions that violate T symmetry also violate the combined CP symmetry, where C represents charge conjugation—the transformation from particle to antiparticle. A longstanding mystery in physics is the origin of the matter–antimatter asymmetry of the Universe, and the missing ingredient is a currently unknown source of CP violation [7]. This mystery has inspired searches for CP-violating effects in neutrino physics and for CP-violating permanent electric dipole moments of the electron and other elementary particles. The possibility that gravity could violate CP symmetry adds yet further motivation to probe spin–gravity interactions.
Substantial theoretical efforts, beginning shortly after Einstein’s development of general relativity, have shown that including intrinsic spin in general relativity’s framework can alter the theory in fundamental ways [8]. Given that intrinsic spin is ultimately a form of angular momentum, one could expect by analogy that gravitational effects on orbital angular momentum would have equivalent effects on spin. This concept suggests an interesting test. General relativity predicts that rotating massive bodies drag spacetime around with them as they rotate. This so-called frame dragging causes gyroscopes to precess—an effect measured, for example, by the Gravity Probe B mission [9]. The sensitivity of the USTC experiment is still many orders of magnitude away from being able to measure spin precession caused by frame dragging. Yet there are experimental proposals suggesting that such a test might someday be possible [10].
References
- S.-B. Zhang et al., “Search for spin-dependent gravitational interactions at Earth range,” Phys. Rev. Lett. 130, 201401 (2023).
- E. D. Commins, “Electron spin and its history,” Annu. Rev. Nucl. Part. Sci. 62, 133 (2012).
- A. Peres, “Test of equivalence principle for particles with spin,” Phys. Rev. D 18, 2739 (1978).
- J. E. Moody and F. Wilczek, “New macroscopic forces?” Phys. Rev. D 30, 130 (1984).
- The Search for Ultralight Bosonic Dark Matter, edited by D. F. Jackson Kimball and K. van Bibber (Springer, Cham, 2022)[Amazon][WorldCat].
- J. Leitner and S. Okubo, “Parity, charge conjugation, and time reversal in the gravitational interaction,” Phys. Rev. 136, B1542 (1964).
- A. D. Sakharov, “Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe,” Zh. Eksp. Teor. Fiz., Pis’ma Red. 5, 32 (1967).
- F. W. Hehl et al., “General relativity with spin and torsion: Foundations and prospects,” Rev. Mod. Phys. 48, 393 (1976).
- C. W. F. Everitt et al., “Gravity Probe B: Final results of a space experiment to test general relativity,” Phys. Rev. Lett. 106, 221101 (2011).
- P. Fadeev et al., “Gravity Probe Spin: Prospects for measuring general-relativistic precession of intrinsic spin using a ferromagnetic gyroscope,” Phys. Rev. D 103, 044056 (2021).