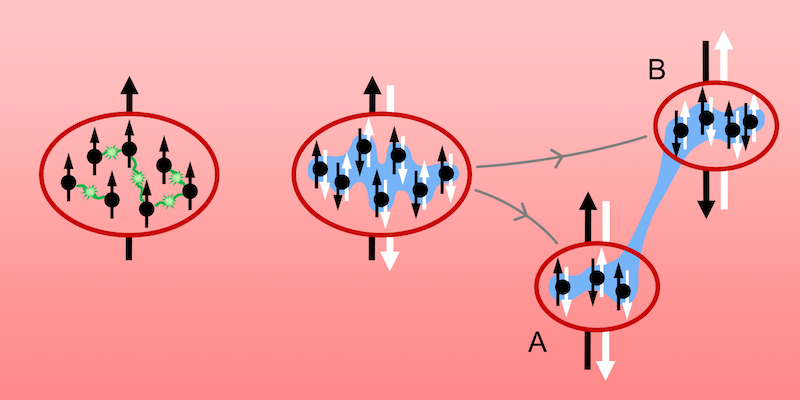
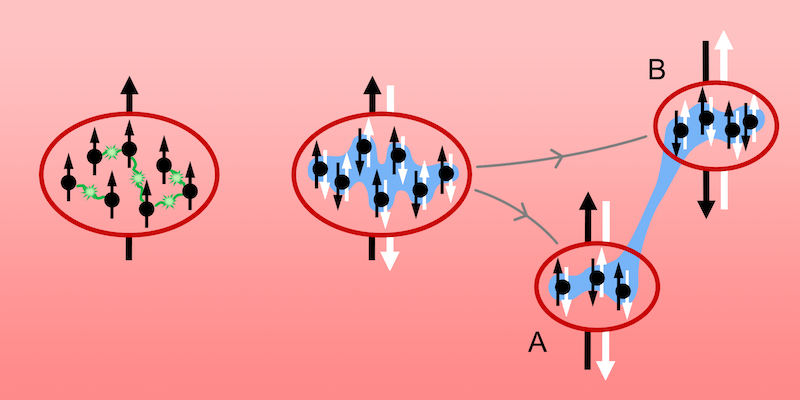
Realizing the Einstein-Podolsky-Rosen Paradox for Atomic Clouds
In 1935, Einstein, Podolsky, and Rosen (EPR) presented an argument that they claimed implies that quantum mechanics provides an incomplete description of reality [1]. The argument rests on two assumptions. First, if the value of a physical property of a system can be predicted with certainty, without disturbance to the system, then there is an “element of reality” to that property, meaning it has a value even if it isn’t measured. Second, physical processes have effects that act locally rather than instantaneously over a distance. John Bell subsequently proposed a way to experimentally test these “local realism” assumptions [2], and so-called Bell tests have since invalidated them for systems of a few small particles, such as electrons or photons [3]. Now Paolo Colciaghi and colleagues at the University of Basel, Switzerland, have tested EPR’s argument for a larger system comprising clouds of hundreds of atoms [4]. Their results bring into question the validity of EPR’s local realism for mesoscopic massive systems.
EPR considered a system of two spatially separated particles, A and B, that have pairs of noncommuting observables, such as their position and momentum. The systems are prepared so that the particles’ positions are correlated and their momenta are anticorrelated. This relationship between observables means that an experimentalist should be able to determine the position or momentum of particle A with certainty by making the appropriate measurement of B. Importantly, the system is set up so that the particles are “space-like separated,” meaning there can be no disturbance of A because of a measurement at B.
Assuming local realism, EPR concluded that the particles’ positions and momenta are both simultaneously well-defined. But quantum mechanics does not allow simultaneous, precisely defined values for both position and momentum. EPR proposed to resolve this paradox by suggesting that quantum mechanics is incomplete, implying that a full theory would include what physicists now term local hidden variables—a possibility that Bell tests have since ruled out [2, 3].
Whereas most Bell tests have been conducted on pairs of individual particles, Colciaghi and colleagues use clouds of several hundred rubidium-87 atoms. They start by preparing a single Bose-Einstein condensate in a trap and engineer an interaction to entangle the condensate’s atoms (Fig. 1). Once released from the trap, the condensate expands to form two entangled clouds separated by up to 100 µm. In order to test the paradox, it is necessary to measure two noncommuting observables. Instead of using position and momentum as envisaged by EPR, Colciaghi and colleagues use “pseudospins”—a pair of quantum states that, like spin, constitute a two-level system. These “spins” are defined by two hyperfine levels, with the spin of each cloud determined by the number of atoms in one level minus the number of atoms in the other level. To measure the first of the noncommuting spin observables, the atoms in each level are counted directly. The second, complementary spin observable is measured using a pulse that interacts with the atoms prior to the count. EPR tests using atomic ensembles have been conducted before [5–7], but here there is an important difference: In this experiment, the choice of measurement settings—meaning which of the two noncommuting spins is measured—is made independently for each cloud. This independence is essential for a genuine EPR paradox; without it we cannot rule out an influence between the systems [8].
Colciaghi and colleagues probe EPR correlations by determining the errors in inferring the spin of cloud A from measurements of the spin of cloud B, first when the pulses are absent, and then again when the pulses are applied for both A and B. While not zero, the product of these errors is small relative to the lower bound of the Heisenberg uncertainty product measured in the experiment. The paradox is therefore confirmed, since the noncommuting spins for A can be inferred with a precision not quantifiable by any local quantum state for A [9]. Yet, if these correlations are the result of a measurement made at B somehow affecting the outcome at A by nonclassical means, then the experiment, which involves a large number of atoms, is intriguingly macroscopic.
The researchers then make a very revealing modification to their experiment. In 1935, Schrödinger responded to EPR’s argument with his famous example of the cat in a superposition state [10]. Less well known is his proposal of a situation in which the measurement settings are adjusted so that two complementary variables are measured simultaneously, “one by direct, the other by indirect measurement.” Schrödinger pondered whether the values for both variables would be precisely determined for this choice of measurement settings (when the settings are fixed but prior to the measurement being finalized), and he questioned whether this determination of values would be compatible with quantum mechanics. Colciaghi and colleagues create such a scenario by manipulating the pulses that determine which spin is measured: Keeping the setting of cloud B fixed, they change the setting of cloud A.
The researchers show that they can measure the value of one variable of cloud A directly, while inferring the value of the complementary variable indirectly from a measurement on cloud B. Furthermore, by adjusting the setting of A again, they show how the correlation with the measurement at B is regained. This illustrates that changing the setting of cloud A does not change the correctness of the prediction made for the complementary variable at A by measuring B. Does this finding imply that there is an element of reality for the outcome of the measurement at A once the setting at B is fixed? For the direct measurement of each variable, the system is prepared for the counting of atoms in the two levels after any interaction of the atoms with the pulses, when the measurement settings are determined. Are the atoms that would be counted already in those levels, whether or not the count takes place? The mesoscopic nature of the experiment would appear to strengthen Schrödinger’s argument: It seems that the values of the observables would be fixed once the measurement settings are determined but before the measurements are finalized by counting the atoms.
The implications of the results are not completely clear. To confirm the indirectly obtained value at A requires a further interaction to change the setting, which means the quantum state changes. Hence, the proposition that the values for both spins are determined prior to the measurement does not violate the uncertainty principle; nor are the values excluded by Bell’s theorem, which refers to variables defined prior to the interactions that fix the settings. Yet, as Schrödinger observed, it seems that—according to quantum mechanics—after the indirect measurement at B, the system A is described by a wave function for which the indirectly measured value is, as Schrödinger put it, “fully sharp,” but the directly measured value is “fully indeterminate” [10]. Schrödinger further questioned the legitimacy of the simultaneous values for position x and for momentum p by proving that the value of x2 + p2, when the two observables are measured simultaneously, must be an odd integer number—despite x and p being continuous and therefore apparently not subject to this restriction [10]. Such questions remain open and may well be elucidated by a closer examination of the recent experiment.
References
- A. Einstein et al., “Can quantum-mechanical description of physical reality be considered complete?” Phys. Rev. 47, 777 (1935).
- J. S. Bell, “On the Einstein Podolsky Rosen paradox,” Physics 1, 195 (1964).
- N. Brunner et al., “Bell nonlocality,” Rev. Mod. Phys. 86, 419 (2014).
- P. Colciaghi et al., “Einstein-Podolsky-Rosen experiment with two Bose-Einstein condensates,” Phys. Rev. X 13, 021031 (2023).
- J. Peise et al., “Satisfying the Einstein–Podolsky–Rosen criterion with massive particles,” Nat. Commun. 6, 8984 (2015).
- M. Fadel et al., “Spatial entanglement patterns and Einstein-Podolsky-Rosen steering in Bose-Einstein condensates,” Science 360, 409 (2018).
- P. Kunkel et al., “Spatially distributed multipartite entanglement enables EPR steering of atomic clouds,” Science 360, 413 (2018).
- A. Aspect et al., “Experimental test of Bell’s inequalities using time-varying analyzers,” Phys. Rev. Lett. 49, 1804 (1982).
- M. D. Reid et al., “Colloquium: The Einstein-Podolsky-Rosen paradox: From concepts to applications,” Rev. Mod. Phys. 81, 1727 (2009).
- E. Schrödinger, “Die gegenwärtige Situation in der Quantenmechanik,” Naturwissenschaften 23, 844 (1935), [“The current situation in quantum mechanics,” Sci. Nat. 23, 844 (1935)].