Environmental Noise Makes a Sensor More Sensitive
Sensors of all kinds, from accelerometers to thermometers, may be hampered by random fluctuations (noise) in the environment, which can swamp the signals they aim to detect. But a new study shows how noise might actually be used to improve the sensitivity of sensors [1]. In experiments using a wireless wearable sensor that monitors a person’s breathing during exercise, the researchers showed that the sensor’s ability to detect weak signals is greatest not when the input is noise-free but when it includes a modest amount of noise.
Most attempts to deal with the detrimental effects of noise in sensing focus on reducing or removing it, for example, using filtering or active noise cancellation. However, it has long been known that some nonlinear systems—where the output signal is not simply proportional to the input—can benefit from noise through an effect called stochastic resonance [2]. This phenomenon, where a modest amount of noise actually boosts the output, is exploited by some biological systems, such as organs in crayfish that detect motion [3]. Stochastic resonance has also been reported in various specialized electronic circuits and mechanical devices.
Now a team in Singapore and China, led by electronics engineer John Ho of the National University of Singapore, has shown how to induce stochastic resonance to improve sensitivity in a mechanical sensor. The key is to operate the device close to a so-called exceptional point (EP), where the nonlinearity is particularly strong.
EPs occur in resonating systems that can exchange energy with their environments. Such systems may have resonant frequencies at which they naturally vibrate in the absence of a periodic driving force—for example, a bridge that vibrates in response to wind. Two such resonant frequencies (called eigenfrequencies) may coincide when some other property of the system reaches a certain value. This coalescence occurs at an EP and can induce highly nonlinear behavior, so that the system might show a pronounced response to a small signal.
In their latest research, Ho and colleagues study a resonating sensor that produces an output when the amplitude of the input signal exceeds some threshold. They show theoretically that noise in the input can induce EPs at random moments, whereupon the sensor becomes temporarily more sensitive—an input signal initially too weak to induce an output signal can now do so. In this way, the noise boosts the sensor’s overall performance by stochastic resonance: the greatest signal-to-noise ratio is not at zero noise but at some particular amplitude of noise.
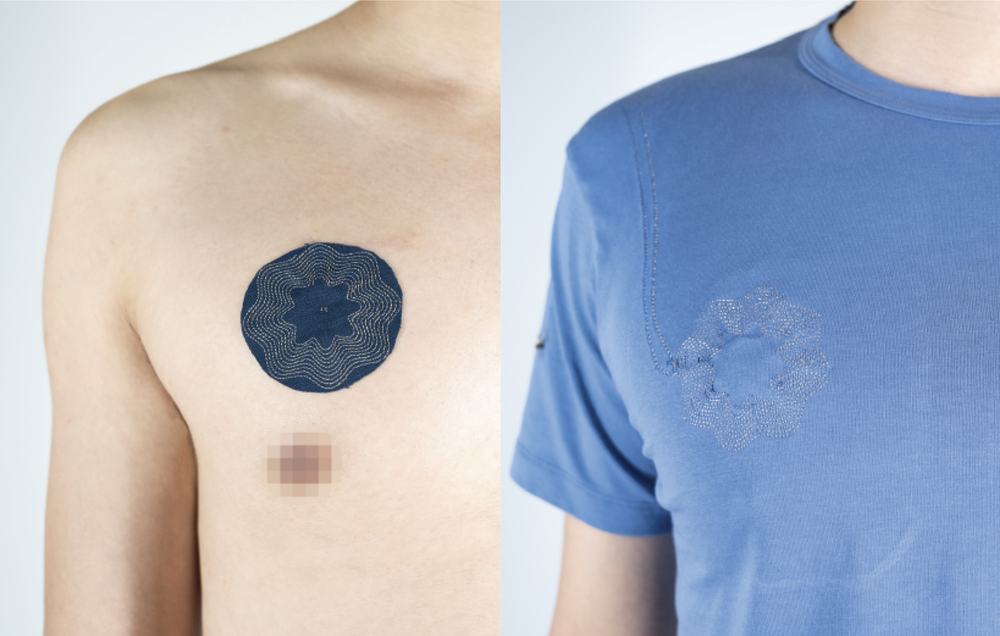
To test the idea experimentally, the researchers used a movement sensor consisting of two pairs of overlaid, oval patches of silver thread woven into a textile. One pair is worn on the skin and the other on a garment placed over the first. The electrically conductive patches can act as the charged plates of capacitors in electrical circuits known as LC resonators. When the distance between the two resonators changes because of movements of the wearer—for example, due to breathing—the coupling between them also changes. This change alters the resonant frequency of the patches on the clothing, whose resonance is monitored wirelessly and used as the output signal. Such a device can sense respiration.
In the experiments, as the wearer’s movement became more vigorous, from standing to walking and running, the noisiness of the input increased, inducing stochastic EPs in the sensor, which then created the predicted improvement in sensitivity. The sensor’s signal-to-noise ratio initially increased as the noise level increased, reaching a maximum before declining again as noise swamped the signal: the characteristic signature of stochastic resonance. As a result, the sensor continued to work well for monitoring respiration rate during walking, whereas without the boost from stochastic resonance it could only detect the rate cleanly when the subject was standing still.
Ho and colleagues say that this effect could be exploited to improve healthcare monitoring, being adaptable to sensors for heartbeat, gait, and sweat production, for example. They say it might also improve sensing of environmental parameters such as pressure, temperature, or humidity.
“I am really impressed that [Ho and colleagues] have demonstrated this clever idea in a real-world application,” says Liang Jiang, an expert in quantum sensing at the University of Chicago. “It is really a cool demonstration.” Condensed-matter physicist Mark Dykman of Michigan State University says that exploring the behavior around exceptional points in the presence of noise is valuable. “This is a new item in the long list of ‘unconventional’ stochastic resonance phenomena,” he says.
–Philip Ball
Philip Ball is a freelance science writer in London. His latest book is How Life Works (Picador, 2024).
References
- Z. Li et al., “Stochastic exceptional points for noise-assisted sensing,” Phys. Rev. Lett. 130, 227201 (2023).
- L. Gammaitoni et al., “Stochastic resonance,” Rev. Mod. Phys. 70, 223 (1998).
- J. K. Douglass et al., “Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance,” Nature 365, 337 (1993).